Fejér kernel

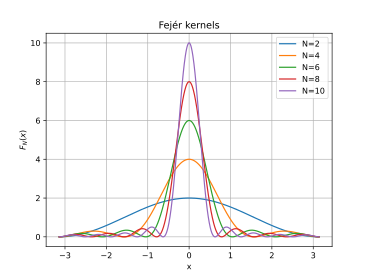
In mathematics, the Fejér kernel is a summability kernel used to express the effect of Cesàro summation on Fourier series. It is a non-negative kernel, giving rise to an approximate identity. It is named after the Hungarian mathematician Lipót Fejér (1880–1959).

The Fejér kernel has many equivalent definitions. Three such definitions are outlined below:

1) The traditional definition expresses the Fejér kernel ${\displaystyle F_n(x)}$ in terms of the Dirichlet kernel

${\displaystyle F_n(x)=\frac{1}{n}{\displaystyle \sum _{k=0}^{n-1}}{D}_k(x)}$

where

${\displaystyle D_k(x)={\displaystyle \sum _{s=-k}^k}{\mathrm{e}}^{isx}}$

is the ${\displaystyle k}$th order Dirichlet kernel.

2) The Fejér kernel ${\displaystyle F_n(x)}$ may also be written in a closed form expression as follows^[1]

${\displaystyle F_n(x)=\frac{1}{n}{\left(\frac{\sin (\frac{nx}{2})}{\sin (\frac{x}{2})}\right)}^2=\frac{1}{n}\left(\frac{1-\cos (nx)}{1-\cos (x)}\right)}$

This closed form expression may be derived from the definitions used above. A proof of this result goes as follows.

Using the fact that the Dirichlet kernel may be written as:^[2]

${\displaystyle D_k(x)=\frac{\sin ((k+\frac{1}{2})x)}{\sin \frac{x}{2}}}$,

one obtains from the definition of the Fejér kernel above:

$${\displaystyle F_n(x)=\frac{1}{n}{\displaystyle \sum _{k=0}^{n-1}}{D}_k(x)=\frac{1}{n}{\displaystyle \sum _{k=0}^{n-1}}\frac{\sin ((k+\frac{1}{2})x)}{\sin (\frac{x}{2})}=\frac{1}{n}\frac{1}{\sin (\frac{x}{2})}{\displaystyle \sum _{k=0}^{n-1}}\sin ((k+\frac{1}{2})x)=\frac{1}{n}\frac{1}{{\sin }^2(\frac{x}{2})}{\displaystyle \sum _{k=0}^{n-1}}[\sin ((k+\frac{1}{2})x)\cdot \sin (\frac{x}{2})]}$$

By the trigonometric identity: ${\displaystyle \sin (\alpha )\cdot \sin (\beta )=\frac{1}{2}(\cos (\alpha -\beta )-\cos (\alpha +\beta ))}$, one has

$${\displaystyle F_n(x)=\frac{1}{n}\frac{1}{{\sin }^2(\frac{x}{2})}{\displaystyle \sum _{k=0}^{n-1}}[\sin ((k+\frac{1}{2})x)\cdot \sin (\frac{x}{2})]=\frac{1}{n}\frac{1}{2{\sin }^2(\frac{x}{2})}{\displaystyle \sum _{k=0}^{n-1}}[\cos (kx)-\cos ((k+1)x)],}$$

which allows evaluation of ${\displaystyle F_n(x)}$ as a telescoping sum:

$${\displaystyle F_n(x)=\frac{1}{n}\frac{1}{{\sin }^2\left(\frac{x}{2}\right)}\frac{1-\cos (nx)}{2}=\frac{1}{n}\frac{1}{{\sin }^2\left(\frac{x}{2}\right)}{\sin }^2\left(\frac{nx}{2}\right)=\frac{1}{n}{\left(\frac{\sin (\frac{nx}{2})}{\sin (\frac{x}{2})}\right)}^2.}$$

3) The Fejér kernel can also be expressed as:

${\displaystyle F_n(x)=\sum _{|k|\le n-1}(1-\frac{|k|}{n})e^{ikx}}$

The Fejér kernel is a positive summability kernel. An important property of the Fejér kernel is ${\displaystyle F_n(x)\ge 0}$ with average value of ${\displaystyle 1}$.

The convolution ${\displaystyle F_n}$ is positive: for ${\displaystyle f\ge 0}$ of period ${\displaystyle 2\pi }$ it satisfies

${\displaystyle 0\le (f*F_n)(x)=\frac{1}{2\pi }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}}f(y)F_n(x-y)dy.}$

Since

${\displaystyle f*D_n=S_n(f)=\sum _{|j|\le n}{\hat{f}}_j{e}^{ijx},}$

we have

${\displaystyle f*F_n=\frac{1}{n}{\displaystyle \sum _{k=0}^{n-1}}{S}_k(f),}$

which is Cesàro summation of Fourier series. By Young's convolution inequality,

${\displaystyle \Vert F_n*f{\Vert }_{L^p([-\pi ,\pi ])}\le \Vert f{\Vert }_{L^p([-\pi ,\pi ])}\text{ for every }1\le p\le \mathrm{\infty }\text{for}f\in L^p.}$

Additionally, if ${\displaystyle f\in L^1([-\pi ,\pi ])}$, then

${\displaystyle f*F_n\to f}$ a.e.

Since ${\displaystyle [-\pi ,\pi ]}$ is finite, ${\displaystyle L^1([-\pi ,\pi ])\supset L^2([-\pi ,\pi ])\supset \cdots \supset L^{\mathrm{\infty }}([-\pi ,\pi ])}$, so the result holds for other ${\displaystyle L^p}$ spaces, ${\displaystyle p\ge 1}$ as well.

If ${\displaystyle f}$ is continuous, then the convergence is uniform, yielding a proof of the Weierstrass theorem.

• One consequence of the pointwise a.e. convergence is the uniqueness of Fourier coefficients: If ${\displaystyle f,g\in L^1}$ with ${\displaystyle \hat{f}=\hat{g}}$, then ${\displaystyle f=g}$ a.e. This follows from writing

${\displaystyle f*F_n=\sum _{|j|\le n}(1-\frac{|j|}{n}){\hat{f}}_j{e}^{ijt},}$

which depends only on the Fourier coefficients.

• A second consequence is that if ${\displaystyle \underset{n\to \mathrm{\infty }}{\lim }{S}_n(f)}$ exists a.e., then ${\displaystyle \underset{n\to \mathrm{\infty }}{\lim }{F}_n(f)=f}$ a.e., since Cesàro means ${\displaystyle F_n*f}$ converge to the original sequence limit if it exists.

The Fejér kernel is used in signal processing and Fourier analysis.

• Fejér's theorem
• Dirichlet kernel
• Gibbs phenomenon
• Charles Jean de la Vallée-Poussin

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Fejér kernel. Read more