Gauss composition law

In mathematics, in number theory, Gauss composition law is a rule, invented by Carl Friedrich Gauss, for performing a binary operation on integral binary quadratic forms (IBQFs). Gauss presented this rule in his Disquisitiones Arithmeticae,^[1] a textbook on number theory published in 1801, in Articles 234 - 244. Gauss composition law is one of the deepest results in the theory of IBQFs and Gauss's formulation of the law and the proofs its properties as given by Gauss are generally considered highly complicated and very difficult.^[2] Several later mathematicians have simplified the formulation of the composition law and have presented it in a format suitable for numerical computations. The concept has also found generalisations in several directions.

Integral binary quadratic forms

An expression of the form [math]\displaystyle{ Q(x,y)=\alpha x^2 + \beta xy + \gamma y^2 }[/math], where [math]\displaystyle{ \alpha, \beta, \gamma, x, y }[/math] are all integers, is called an integral binary quadratic form (IBQF). The form [math]\displaystyle{ Q(x,y) }[/math] is called a primitive IBQF if [math]\displaystyle{ \alpha, \beta, \gamma }[/math] are relatively prime. The quantity [math]\displaystyle{ \Delta = \beta^2-4\alpha\gamma }[/math] is called the discriminant of the IBQF [math]\displaystyle{ Q(x,y) }[/math]. An integer [math]\displaystyle{ \Delta }[/math] is the discriminant of some IBQF if and only if [math]\displaystyle{ \Delta \equiv 0, 1 (\mathrm{mod}\,\, 4) }[/math]. [math]\displaystyle{ \Delta }[/math] is called a fundamental discriminant if and only if one of the following statements holds

• [math]\displaystyle{ \Delta \equiv 1\,\, (\mathrm{mod}\,\, 4) }[/math] and is square-free,
• [math]\displaystyle{ \Delta = 4m }[/math] where [math]\displaystyle{ m=2 \text{ or } 3\,\, (\mathrm{mod}\,\, 4) }[/math] and [math]\displaystyle{ m }[/math] is square-free.

If [math]\displaystyle{ \Delta\lt 0 }[/math] and [math]\displaystyle{ \alpha\gt 0 }[/math] then [math]\displaystyle{ Q(x,y) }[/math] is said to be positive definite; if [math]\displaystyle{ \Delta\lt 0 }[/math] and [math]\displaystyle{ \alpha\lt 0 }[/math] then [math]\displaystyle{ Q(x,y) }[/math] is said to be negative definite; if [math]\displaystyle{ \Delta\gt 0 }[/math] then [math]\displaystyle{ Q(x,y) }[/math] is said to be indefinite.

Equivalence of IBQFs

Two IBQFs [math]\displaystyle{ g(x,y) }[/math] and [math]\displaystyle{ h(x,y) }[/math] are said to be equivalent (or, properly equivalent) if there exist integers α, β, γ, δ such that

[math]\displaystyle{ \alpha\delta - \beta\gamma = 1 }[/math] and [math]\displaystyle{ g(\alpha x + \beta y, \gamma x + \delta y) = h(x,y). }[/math]

The notation [math]\displaystyle{ g(x,y) \sim h(x,y) }[/math] is used to denote the fact that the two forms are equivalent. The relation "[math]\displaystyle{ \sim }[/math]" is an equivalence relation in the set of all IBQFs. The equivalence class to which the IBQF [math]\displaystyle{ g(x,y) }[/math] belongs is denoted by [math]\displaystyle{ [g(x,y)] }[/math].

Two IBQFs [math]\displaystyle{ g(x,y) }[/math] and [math]\displaystyle{ h(x,y) }[/math] are said to be improperly equivalent if

[math]\displaystyle{ \alpha\delta - \beta\gamma = -1 }[/math] and [math]\displaystyle{ g(\alpha x + \beta y, \gamma x + \delta y) = h(x,y). }[/math]

The relation in the set of IBQFs of being improperly equivalent is also an equivalence relation.

It can be easily seen that equivalent IBQFs (properly or improperly) have the same discriminant.

Gauss's formulation of the composition law

Historical context

The following identity, called Brahmagupta identity, was known to the Indian mathematician Brahmagupta (598–668) who used it to calculate successively better fractional approximations to square roots of positive integers:

[math]\displaystyle{ (x^2 +D y^2)(u^2 + D v^2) = (xu+Dyv)^2 + D(xv - yu)^2 }[/math]

Writing [math]\displaystyle{ f(x,y)=x^2+Dy^2 }[/math] this identity can be put in the form

[math]\displaystyle{ f(x,y)f(u,v)=f(X,Y) }[/math] where [math]\displaystyle{ X = xu+Dyv, Y=xv-yu }[/math].

Gauss's composition law of IBQFs generalises this identity to an identity of the form [math]\displaystyle{ g(x,y)h(u,v)=F(X,Y) }[/math] where [math]\displaystyle{ g(x,y), h(x,y), F(X,Y) }[/math] are all IBQFs and [math]\displaystyle{ X,Y }[/math] are linear combinations of the products [math]\displaystyle{ xu, xv, yu, yv }[/math].

The composition law of IBQFs

Consider the following IBQFs:

[math]\displaystyle{ g(x,y) = ax^2+bxy+cy^2 }[/math]

[math]\displaystyle{ h(x,y) = dx^2+exy+ fy^2 }[/math]

[math]\displaystyle{ F(x,y) = Ax^2 + Bxy + Cy^2 }[/math]

If it is possible to find integers [math]\displaystyle{ p,q,r,s }[/math] and [math]\displaystyle{ p^\prime, q^\prime, r^\prime, s^\prime }[/math] such that the following six numbers

[math]\displaystyle{ pq^\prime - qp^\prime, pr^\prime - rp^\prime, ps^\prime - sp^\prime, qr^\prime - rq^\prime, qs^\prime - sq^\prime, rs^\prime - sr^\prime }[/math]

have no common divisors other than ±1, and such that if we let

[math]\displaystyle{ X = pxu + qxv + ryu+syv }[/math]

[math]\displaystyle{ Y = p^\prime xu + q^\prime xv + r^\prime yu+s^\prime yv }[/math]

the following relation is identically satisfied

[math]\displaystyle{ g(x,y)h(u,v) = F(X,Y) }[/math],

then the form [math]\displaystyle{ F(x,y) }[/math] is said to be a composite of the forms [math]\displaystyle{ g(x,y) }[/math] and [math]\displaystyle{ h(x, y) }[/math]. It may be noted that the composite of two IBQFs, if it exists, is not unique.

Example

Consider the following binary quadratic forms:

[math]\displaystyle{ g(x,y) = 2x^2+3xy-10y^2 }[/math]

[math]\displaystyle{ h(x,y) = 5x^2 + 3xy-4y^2 }[/math]

[math]\displaystyle{ F(x,y) = 10x^2 +3xy - 2 y^2 }[/math]

Let

[math]\displaystyle{ [p, q, r, s] = [1, 0, 0, 2], \quad [p^\prime, q^\prime, r^\prime, s^\prime] =[0, 2, 5, 3] }[/math]

We have

[math]\displaystyle{ pq^\prime - qp^\prime=2, pr^\prime - rp^\prime=5, ps^\prime - sp^\prime=3, qr^\prime - rq^\prime=0, qs^\prime - sq^\prime=4, rs^\prime - sr^\prime=10 }[/math].

These six numbers have no common divisors other than ±1. Let

[math]\displaystyle{ X = pxu + qxv + ryu+syv = xu+2yv }[/math],

[math]\displaystyle{ Y = p^\prime xu + q^\prime xv + r^\prime yu+s^\prime yv = 2xv+5yu+3yv }[/math].

Then it can be verified that

[math]\displaystyle{ g(x,y)h(u,v) = F(X,Y) }[/math].

Hence [math]\displaystyle{ F(x,y) }[/math] is a composite of [math]\displaystyle{ g(x,y) }[/math] and [math]\displaystyle{ h(x, y) }[/math].

An algorithm to find the composite of two IBQFs

The following algorithm can be used to compute the composite of two IBQFs.^[3]

Algorithm

Given the following IBQFs having the same discriminant [math]\displaystyle{ \Delta }[/math]:

[math]\displaystyle{ f_1(x,y) = a_1x^2+b_1xy+c_1y^2 }[/math]

[math]\displaystyle{ f_2(x,y) = a_2x^2 + b_2xy + c_2y^2 }[/math]

[math]\displaystyle{ \Delta=b_1^2-4a_1c_1=b_2^2-4a_2c_2 }[/math]

1. Compute [math]\displaystyle{ \beta = \frac{b_1+b_2}{2} }[/math]
2. Compute [math]\displaystyle{ n = \gcd (a_1,a_2,\beta) }[/math]
3. Compute [math]\displaystyle{ t,u,v }[/math] such that [math]\displaystyle{ a_1t+a_2 u+\beta v = n }[/math]
4. Compute [math]\displaystyle{ A = \frac{a_1a_2}{n^2} }[/math]
5. Compute [math]\displaystyle{ B = \frac{a_1b_2t + a_2b_1u + v(b_1b_2+\Delta)/2}{n} }[/math]
6. Compute [math]\displaystyle{ C = \frac{B^2 - \Delta}{4A} }[/math]
7. Compute [math]\displaystyle{ F(x,y) = Ax^2 + Bxy + Cy^2 }[/math]
8. Compute

[math]\displaystyle{ X = nx_1x_2 + \frac{(b_2-B)n}{2a_2} x_1y_2 + \frac{(b_1-B)n}{2a_1} y_1 x_1+ \frac{[b_1b_2+\Delta - B(b_1+b_2)]n}{4a_1a_2} y_1y_2 }[/math]

[math]\displaystyle{ Y = \frac{a_1}{n} x_1y_2 + \frac{a_2}{n}y_1 x_1+ \frac{b_1+b_2}{2n} y_1y_2 }[/math]

Then [math]\displaystyle{ F(X,Y) = f_1(x_1,y_1)f_2(x_2,y_2) }[/math] so that [math]\displaystyle{ F(x,y) }[/math] is a composite of [math]\displaystyle{ f_1(x,y) }[/math] and [math]\displaystyle{ f_2(x,y) }[/math].

Properties of the composition law

Existence of the composite

The composite of two IBQFs exists if and only if they have the same discriminant.

Equivalent forms and the composition law

Let [math]\displaystyle{ g(x,y), h(x,y), g^\prime(x,y), h^\prime(x,y) }[/math] be IBQFs and let there be the following equivalences:

[math]\displaystyle{ g(x,y) \sim g^\prime (x,y) }[/math]

[math]\displaystyle{ h(x,y) \sim h^\prime (x,y) }[/math]

If [math]\displaystyle{ F(x,y) }[/math] is a composite of [math]\displaystyle{ g(x,y) }[/math] and [math]\displaystyle{ h(x,y) }[/math], and [math]\displaystyle{ F^\prime(x,y) }[/math] is a composite of [math]\displaystyle{ g^\prime(x,y) }[/math] and [math]\displaystyle{ h^\prime(x,y) }[/math], then

[math]\displaystyle{ F(x,y) \sim F^\prime (x,y). }[/math]

A binary operation

Let [math]\displaystyle{ D }[/math] be a fixed integer and consider set [math]\displaystyle{ S_D }[/math] of all possible primitive IBQFs of discriminant [math]\displaystyle{ D }[/math]. Let [math]\displaystyle{ G_D }[/math] be the set of equivalence classes in this set under the equivalence relation "[math]\displaystyle{ \sim }[/math]". Let [math]\displaystyle{ [g(x,y)] }[/math] and [math]\displaystyle{ [h(x,y)] }[/math] be two elements of [math]\displaystyle{ G_D }[/math]. Let [math]\displaystyle{ F(x,y) }[/math] be a composite of the IBQFs [math]\displaystyle{ g(x,y) }[/math] and [math]\displaystyle{ h(x,y) }[/math] in [math]\displaystyle{ S_D }[/math]. Then the following equation

[math]\displaystyle{ [g(x,y)] \circ [h(x,y)] = [F(x,y)] }[/math]

defines a well-defined binary operation "[math]\displaystyle{ \circ }[/math]" in [math]\displaystyle{ G_D }[/math].

The group G_D

• The set [math]\displaystyle{ G_D }[/math] is a finite abelian group under the binary operation [math]\displaystyle{ \circ }[/math].

• The identity element in the group [math]\displaystyle{ G_D }[/math] = [math]\displaystyle{ \begin{cases} [x^2-(D/4)y^2] & \text{ if } D \equiv 0\,(\mathrm{mod}\,\, 4)\\[1mm] [x^2+xy+((1-D)/4)y^2] & \text{ if } D \equiv 1\, (\mathrm{mod}\,\, 4) \end{cases} }[/math]

• The inverse of [math]\displaystyle{ [ax^2+bxy+cy^2] }[/math] in [math]\displaystyle{ G_D }[/math] is [math]\displaystyle{ [ax^2 -bxy+cy^2] }[/math].

Modern approach to the composition law

The following sketch of the modern approach to the composition law of IBQFs is based on a monograph by Duncan A. Buell.^[4] The book may be consulted for further details and for proofs of all the statements made hereunder.

Quadratic algebraic numbers and integers

Let [math]\displaystyle{ \mathbb Z }[/math] be the set of integers. Hereafter, in this section, elements of [math]\displaystyle{ \mathbb Z }[/math] will be referred as rational integers to distinguish them from algebraic integers to be defined below.

A complex number [math]\displaystyle{ \alpha }[/math] is called a quadratic algebraic number if it satisfies an equation of the form

[math]\displaystyle{ ax^2+bx+c=0 }[/math] where [math]\displaystyle{ a,b,c \in \mathbb Z }[/math].

[math]\displaystyle{ \alpha }[/math] is called a quadratic algebraic integer if it satisfies an equation of the form

[math]\displaystyle{ x^2+bx+c=0 }[/math] where [math]\displaystyle{ b, c \in \mathbb Z }[/math]

The quadratic algebraic numbers are numbers of the form

[math]\displaystyle{ \alpha = \frac{-b +e\sqrt{d}}{2a} }[/math] where [math]\displaystyle{ a,b,d,e \in \mathbb Z }[/math] and [math]\displaystyle{ d }[/math] has no square factors other than [math]\displaystyle{ 1 }[/math].

The integer [math]\displaystyle{ d }[/math] is called the radicand of the algebraic integer [math]\displaystyle{ \alpha }[/math]. The norm of the quadratic algebraic number [math]\displaystyle{ \alpha }[/math] is defined as

[math]\displaystyle{ N(\alpha) = (b^2+e^2d)/4a^2 }[/math].

Let [math]\displaystyle{ \mathbb Q }[/math] be the field of rational numbers. The smallest field containing [math]\displaystyle{ \mathbb Q }[/math] and a quadratic algebraic number [math]\displaystyle{ \alpha }[/math] is the quadratic field containing [math]\displaystyle{ \alpha }[/math] and is denoted by [math]\displaystyle{ \mathbb Q (\alpha) }[/math]. This field can be shown to be

[math]\displaystyle{ \mathbb Q (\alpha) = \mathbb Q (\sqrt{d}) = \{ t+u\sqrt{d}\,|\, t,u \in \mathbb Q\} }[/math]

The discriminant [math]\displaystyle{ \Delta }[/math] of the field [math]\displaystyle{ \mathbb Q(\sqrt{d}) }[/math] is defined by

[math]\displaystyle{ \Delta = \begin{cases} 4d & \text{ if } d \equiv 2 \text{ or } 3 \,\, (\mathrm{mod}\,\, 4 )\\[1mm] d & \text{ if } d \equiv 1 \,\, (\mathrm{mod}\,\, 4 ) \end{cases} }[/math]

Let [math]\displaystyle{ d \ne 1 }[/math] be a rational integer without square factors (except 1). The set of quadratic algebraic integers of radicand [math]\displaystyle{ d }[/math] is denoted by [math]\displaystyle{ O(\sqrt{d}) }[/math]. This set is given by

[math]\displaystyle{ O(\sqrt{d}) = \begin{cases} \{ a+ b \sqrt{d}\, |\, a,b \in \mathbb Z\} & \text{ if } d \equiv 2\text{ or }3 \,\,(\mathrm{mod}\,\,4)\\[1mm] \{ (a+ b \sqrt{d})/2\, |\, a,b \in \mathbb Z, a\equiv b \,\,\mathrm{mod}\,\, 2)\} & \text{ if } d \equiv 1 \,\,(\mathrm{mod}\,\,4)\} \end{cases} }[/math]

[math]\displaystyle{ O(\sqrt{d}) }[/math] is a ring under ordinary addition and multiplication. If we let

[math]\displaystyle{ \delta = \begin{cases} -\sqrt{d} & \text{ if } \delta \text{ is even}\\[1mm] (1-\sqrt{d})/2 & \text{ if } \delta \text{ is odd} \end{cases} }[/math]

then

[math]\displaystyle{ O(\sqrt{d}) = \{ a + b\delta,|, a,b \in \mathbb Z\} }[/math].

Ideals in quadratic fields

Let [math]\displaystyle{ \mathbf a }[/math] be an ideal in the ring of integers [math]\displaystyle{ O(\sqrt{d}) }[/math]; that is, let [math]\displaystyle{ \mathbf a }[/math] be a nonempty subset of [math]\displaystyle{ O(\sqrt{d}) }[/math] such that for any [math]\displaystyle{ \alpha,\beta \in \mathbf a }[/math] and any [math]\displaystyle{ \lambda, \mu \in O(\sqrt{d}) }[/math], [math]\displaystyle{ \lambda\alpha + \mu\beta \in \mathbf a }[/math]. (An ideal [math]\displaystyle{ \mathbf a }[/math] as defined here is sometimes referred to as an integral ideal to distinguish from fractional ideal to be defined below.) If [math]\displaystyle{ \mathbf a }[/math] is an ideal in [math]\displaystyle{ O(\sqrt{d}) }[/math] then one can find [math]\displaystyle{ \alpha_1, \alpha_2 \in O(\sqrt{d}) }[/math] such any element in [math]\displaystyle{ \mathbf a }[/math] can be uniquely represented in the form [math]\displaystyle{ \alpha_1 x + \alpha_2 y }[/math] with [math]\displaystyle{ x,y\in \mathbb Z }[/math]. Such a pair of elements in [math]\displaystyle{ O(\sqrt{d}) }[/math] is called a basis of the ideal [math]\displaystyle{ \mathbf a }[/math]. This is indicated by writing [math]\displaystyle{ \mathbf a = \langle \alpha_1, \alpha_2 \rangle }[/math]. The norm of [math]\displaystyle{ \mathbf a = \langle \alpha_1, \alpha_2 \rangle }[/math] is defined as

[math]\displaystyle{ N(\mathbf a) = |\alpha_1\overline{\alpha_2} - \overline{\alpha_1}\alpha_2|/\sqrt{\Delta} }[/math].

The norm is independent of the choice of the basis.

Some special ideals

• The product of two ideals [math]\displaystyle{ \mathbf a = \langle \alpha_1, \alpha_2 \rangle }[/math] and [math]\displaystyle{ \mathbf b = \langle \beta_1, \beta_2 \rangle }[/math], denoted by [math]\displaystyle{ \mathbf a \mathbf b }[/math], is the ideal generated by the [math]\displaystyle{ \mathbb Z }[/math]-linear combinations of [math]\displaystyle{ \alpha_1\beta_1, \alpha_1\beta_2, \alpha_2\beta_1, \alpha_2\beta_2 }[/math].

• A fractional ideal is a subset [math]\displaystyle{ I }[/math] of the quadratic field [math]\displaystyle{ \mathbb Q(\sqrt{\Delta}) }[/math] for which the following two properties hold:

1. For any [math]\displaystyle{ \alpha, \beta \in I }[/math] and for any [math]\displaystyle{ \lambda, \mu \in O(\sqrt{d}) }[/math], [math]\displaystyle{ \lambda \alpha + \mu \beta \in I }[/math].
2. There exists a fixed algebraic integer [math]\displaystyle{ \nu }[/math] such that for every [math]\displaystyle{ \alpha \in I }[/math], [math]\displaystyle{ \nu \alpha \in O(\sqrt{d}) }[/math].

• An ideal [math]\displaystyle{ \mathbf a }[/math] is called a principal ideal if there exists an algebraic integer [math]\displaystyle{ \alpha }[/math] such that [math]\displaystyle{ \mathbf a = \{ \lambda \alpha\, | \, \lambda \in O(\sqrt{d}) \} }[/math]. This principal ideal is denoted by [math]\displaystyle{ (\alpha) }[/math].

There is this important result: "Given any ideal (integral or fractional) [math]\displaystyle{ \mathbf a }[/math], there exists an integral ideal [math]\displaystyle{ \mathbf b }[/math] such that the product ideal [math]\displaystyle{ \mathbf{ab} }[/math] is a principal ideal."

An equivalence relation in the set of ideals

Two (integral or fractional) ideals [math]\displaystyle{ \mathbf a }[/math] and [math]\displaystyle{ \mathbf b }[/math] ares said to be equivalent, dented [math]\displaystyle{ \mathbf a \sim \mathbf b }[/math], if there is a principal ideal [math]\displaystyle{ (\alpha) }[/math] such that [math]\displaystyle{ \mathbf a = (\alpha)\mathbf b }[/math]. These ideals are narrowly equivalent if the norm of [math]\displaystyle{ \alpha }[/math] is positive. The relation, in the set of ideals, of being equivalent or narrowly equivalent as defined here is indeed an equivalence relation.

The equivalence classes (respectively, narrow equivalence classes) of fractional ideals of a ring of quadratic algebraic integers [math]\displaystyle{ O(\sqrt{d}) }[/math] form an abelian group under multiplication of ideals. The identity of the group is the class of all principal ideals (respectively, the class of all principal ideals [math]\displaystyle{ (\alpha) }[/math] with [math]\displaystyle{ N(\alpha)\gt 0 }[/math]). The groups of classes of ideals and of narrow classes of ideals are called the class group and the narrow class group of the [math]\displaystyle{ \mathbb Q(\sqrt{d}) }[/math].

Binary quadratic forms and classes of ideals

The main result that connects the IBQFs and classes of ideals can now be stated as follows:

"The group of classes of binary quadratic forms of discriminant [math]\displaystyle{ \Delta }[/math] is isomorphic to the narrow class group of the quadratic number field [math]\displaystyle{ \mathbb Q(\sqrt {\Delta}) }[/math]."

Bhargava's approach to the composition law

Bhargava cube with the integers a, b, c, d, e, f, g, h at the corners

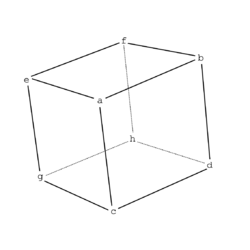
Manjul Bhargava, a Canadian-American Fields Medal winning mathematician introduced a configuration, called a Bhargava cube, of eight integers [math]\displaystyle{ a,b,c,d,e,f }[/math] (see figure) to study the composition laws of binary quadratic forms and other such forms. Defining matrices associated with the opposite faces of this cube as given below

[math]\displaystyle{ M_1=\begin{bmatrix} a & b \\ c & d\end{bmatrix},N_1=\begin{bmatrix} e & f \\ g & h\end{bmatrix}, M_2=\begin{bmatrix} a & c \\ e & g\end{bmatrix},N_2=\begin{bmatrix} b & d \\ f & h\end{bmatrix}, M_3=\begin{bmatrix} a & e \\ b & f\end{bmatrix},N_3=\begin{bmatrix} c & g \\ d & h\end{bmatrix} }[/math],

Bhargava constructed three IBQFs as follows:

[math]\displaystyle{ Q_1=-\det(M_1x+N_1y), \,\,Q_2=-\det(M_2x+N_2y)\,\,Q_3=-\det(M_3x+N_3y) }[/math]

Bhargava established the following result connecting a Bhargava cube with the Gauss composition law:^[5]

"If a cube A gives rise to three primitive binary quadratic forms Q₁, Q₂, Q₃, then Q₁, Q₂, Q₃ have the same discriminant, and the product of these three forms is the identity in the group defined by Gauss composition. Conversely, if Q₁, Q₂, Q₃ are any three primitive binary quadratic forms of the same discriminant whose product is the identity under Gauss composition, then there exists a cube A yielding Q₁, Q₂, Q₃."

References

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Gauss composition law. Read more