Group action (mathematics)

This article includes a list of general references, but it remains largely unverified because it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (April 2015) (Learn how and when to remove this template message)

This article uses first-person ("I"; "we") or second-person ("you") inappropriately. Please rewrite it to use a more formal, encyclopedic tone. (Learn how and when to remove this template message)

In mathematics, a group action on a space is a group homomorphism of a given group into the group of transformations of the space. Similarly, a group action on a mathematical structure is a group homomorphism of a group into the automorphism group of the structure. One says that the group acts on the space or structure. If a group acts on a structure, it also acts on everything that is built on the structure. For example, the group of Euclidean isometries acts on Euclidean space and also on the figures drawn in it. In particular, it acts on the set of all triangles. Similarly, the group of symmetries of a polyhedron acts on the vertices, the edges, and the faces of the polyhedron.

A group action on a (finite-dimensional) vector space is called a representation of the group. It allows one to identifty many groups with subgroups of GL(n, K), the group of the invertible matrices of dimension n over a field K.

The symmetric group S_n acts on any set with n elements by permuting the elements of the set. Although, the group of all permutations of a set depends formally on the set, the concept of group action allows one to consider a single group for studying the permutations of all sets with the same cardinality.

If G is a group and X is a set, then a (left) group action ${\displaystyle \phi }$ of G on X is a function

${\displaystyle \phi :G\times X\to X,(g,x)\mapsto \phi (g,x)}$

that satisfies the following two axioms:^[1]

• Identity:            ${\displaystyle \mathrm{\forall }x\in X,\phi (e,x)=x}$ (here, e denotes the identity element of G.)
• Compatibility:   ${\displaystyle \mathrm{\forall }g,h\in G,\mathrm{\forall }x\in X,\phi (gh,x)=\phi (g,\phi (h,x))}$

The group G is said to act on X (from the left). The set X is called a (left) G-set.

From these two axioms, it follows that for every g in G, the function which maps x in X to ${\displaystyle \phi (g,x)}$ is a bijective map from X to X (its inverse being the function which maps x to ${\displaystyle \phi (g^{-1},x)}$). Therefore, one may alternatively define a group action of G on X as a group homomorphism from G into the symmetric group Sym(X) of all bijections from X to X.^[2]

In complete analogy, one can define a right group action of G on X as a function ${\displaystyle \phi :X\times G\to X,(x,g)\mapsto \phi (x,g)}$ satisfying the axioms

• Identity:            ${\displaystyle \mathrm{\forall }x\in X,\phi (x,e)=x}$
• Compatibility:   ${\displaystyle \mathrm{\forall }g,h\in G,x\in X,\phi (x,gh)=\phi (\phi (x,g),h)}$

The difference between left and right actions is in the order in which a product gh acts on x; for a left action, h acts first and is followed by g, while for a right action, g acts first and is followed by h. Because of the formula (gh)^-1 = h^-1g^-1, one can construct a left action from a right action by composing with the inverse operation of the group. Also, a right action of a group G on X is the same thing as a left action of its opposite group G^op on X. Thus it is sufficient to only consider left actions without any loss of generality.

When there is a natural correspondence between the set of group elements and the set of space transformations, a group can be interpreted as acting on the space in a canonical way. For example, the symmetric group of a finite set consists of all bijective transformations of that set; thus, applying any element of the permutation group to an element of the set will produce another (not necessarily distinct) element of the set. More generally, symmetry groups such as the homeomorphism group of a topological space or the general linear group of a vector space, as well as their subgroups, also admit canonical actions. For other groups, an interpretation of the group in terms of an action may have to be specified, either because the group does not act canonically on any space or because the canonical action is not the action of interest. For example, we can specify an action of the two-element cyclic group C₂ = {0, 1} on the finite set {a, b, c} by specifying that 0 (the identity element) sends a ↦ a, b ↦ b, and c ↦ c, and that 1 sends a ↦ b, b ↦ a, and c ↦ c. This action is not canonical.

The action of G on X is called:

• Transitive if X is non-empty and if for each pair x, y in X there exists a g in G such that g⋅x = y. For example, the action of the symmetric group of X is transitive, the action of the general linear group or the special linear group of a vector space V on V∖{0} is transitive, but the action of the orthogonal group of a Euclidean space E is not transitive on E∖{0} (it is transitive on the unit sphere of E, though).

• Faithful (or effective) if for every two distinct g, h in G there exists an x in X such that g⋅x ≠ h⋅x; or equivalently, if for each g ≠ e in G there exists an x in X such that g⋅x ≠ x. In other words, in a faithful group action, different elements of G induce different permutations of X.^{[lower-alpha 1]} In algebraic terms, a group G acts faithfully on X if and only if the corresponding homomorphism to the symmetric group, G → Sym(X), has a trivial kernel. Thus, for a faithful action, G embeds into a permutation group on X; specifically, G is isomorphic to its image in Sym(X). If G does not act faithfully on X, one can easily modify the group to obtain a faithful action. If we define N = {g in G : g⋅x = x for all x in X}, then N is a normal subgroup of G; indeed, it is the kernel of the homomorphism G → Sym(X). The factor group G/N acts faithfully on X by setting (gN)⋅x = g⋅x. The original action of G on X is faithful if and only if N = {e}. The smallest set on which a faithful action can be defined can vary greatly for groups of the same size. For example:
  • Three groups of size 120 are the symmetric group S₅, the icosahedral group, and the cyclic group Z/120Z. The smallest sets on which faithful actions can be defined are of size 5, 12, and 16 respectively.
  • The abelian groups of size 2ⁿ include a cyclic group Z/(2ⁿ)Z as well as (Z/2Z)ⁿ (the direct product of n copies of Z/2Z), but the latter acts faithfully on a set of size 2n, whereas the former cannot act faithfully on a set smaller than itself.

• Free (or semiregular or fixed point free) if, given g, h in G, the existence of an x in X with g⋅x = h⋅x implies g = h. Equivalently: if g is a group element and there exists an x in X with g⋅x = x (that is, if g has at least one fixed point), then g is the identity. Note that a free action on a non-empty set is faithful.

• Regular (or simply transitive or sharply transitive) if it is both transitive and free; this is equivalent to saying that for every two x, y in X there exists precisely one g in G such that g⋅x = y. In this case, X is called a principal homogeneous space for G or a G-torsor. The action of any group G on itself by left multiplication is regular, and thus faithful as well. Every group can, therefore, be embedded in the symmetric group on its own elements, Sym(G). This result is known as Cayley's theorem.

• n-transitive if X has at least n elements, and for all distinct x₁, ..., x_n and all distinct y₁, ..., y_n, there is a g in G such that g⋅x_k = y_k for 1 ≤ k ≤ n. A 2-transitive action is also called doubly transitive, a 3-transitive action is also called triply transitive, and so on. Such actions define interesting classes of subgroups in the symmetric groups: 2-transitive groups and more generally multiply transitive groups. The action of the symmetric group on a set with n elements is always n-transitive; the action of the alternating group is (n−2)-transitive.

• Sharply n-transitive if there is exactly one such g.

• Primitive if it is transitive and preserves no non-trivial partition of X. See primitive permutation group for details.

• Locally free if G is a topological group, and there is a neighbourhood U of e in G such that the restriction of the action to U is free; that is, if g⋅x = x for some x and some g in U then g = e.

Furthermore, if G acts on a topological space X, then the action is:

• Wandering if every point x in X has a neighbourhood U such that ${\displaystyle \{g\in G:g\cdot U\cap U\ne \mathrm{\varnothing }\}}$ is finite.^[3] For example, the action of ${\displaystyle {\mathbb{\mathbb{Z}}}^n}$ on ${\displaystyle {\mathbb{ℝ}}^n}$ by translations is wandering. The action of the modular group on the Poincaré half-plane is also wandering.

• Properly discontinuous if X is a locally compact space and for every compact subset K ⊂ X the set ${\displaystyle \{g\in G:gK\cap K\ne \mathrm{\varnothing }\}}$ is finite. The wandering actions given above are also properly discontinuous. On the other hand, the action of ${\displaystyle \mathbb{\mathbb{Z}}}$ on ${\displaystyle {\mathbb{ℝ}}^2\setminus \{0\}}$ by the linear map ${\displaystyle (x,y)\mapsto (2x,1/2y)}$ is wandering and free but not properly discontinuous.^[4]

• Proper if G is a topological group and the map from ${\displaystyle G\times X\to X\times X:(g,x)\mapsto (g\cdot x,x)}$ is proper.^[5] If G is discrete then properness is equivalent to proper discontinuity for G-actions.

• Said to have discrete orbits if the orbit of each x in X under the action of G is discrete in X.^[3]

• A covering space action if every point x in X has a neighbourhood U such that ${\displaystyle \{g\in G:g\cdot U\cap U\ne \mathrm{\varnothing }\}=e}$.^[6]

If X is a non-zero module over a ring R and the action of G is R-linear then it is said to be

• Irreducible if there is no nonzero proper invariant submodule.

Consider a group G acting on a set X. The orbit of an element x in X is the set of elements in X to which x can be moved by the elements of G. The orbit of x is denoted by G⋅x:

${\displaystyle G\cdot x=\{g\cdot x\mid g\in G\}.}$

The defining properties of a group guarantee that the set of orbits of (points x in) X under the action of G form a partition of X. The associated equivalence relation is defined by saying x ∼ y if and only if there exists a g in G with g⋅x = y. The orbits are then the equivalence classes under this relation; two elements x and y are equivalent if and only if their orbits are the same, that is, G⋅x = G⋅y.

The group action is transitive if and only if it has exactly one orbit, that is, if there exists x in X with G⋅x = X. This is the case if and only if G⋅x = X for all x in X (given that X is non-empty).

The set of all orbits of X under the action of G is written as X/G (or, less frequently: G\X), and is called the quotient of the action. In geometric situations it may be called the orbit space, while in algebraic situations it may be called the space of coinvariants, and written X_G, by contrast with the invariants (fixed points), denoted X^G: the coinvariants are a quotient while the invariants are a subset. The coinvariant terminology and notation are used particularly in group cohomology and group homology, which use the same superscript/subscript convention.

If Y is a subset of X, one writes GY for the set {g⋅y : y ∈ Y and g ∈ G}. The subset Y is said invariant under G if G⋅Y = Y (which is equivalent to G⋅Y ⊆ Y). In that case, G also operates on Y by restricting the action to Y. The subset Y is called fixed under G if g⋅y = y for all g in G and all y in Y. Every subset that is fixed under G is also invariant under G, but not conversely.

Every orbit is an invariant subset of X on which G acts transitively. The action of G on X is transitive if and only if all elements are equivalent, meaning that there is only one orbit.

A G-invariant element of X is x ∈ X such that g⋅x = x for all g ∈ G. The set of all such x is denoted X^G and called the G-invariants of X. When X is a G-module, X^G is the zeroth cohomology group of G with coefficients in X, and the higher cohomology groups are the derived functors of the functor of G-invariants.

Given g in G and x in X with g⋅x = x, one says that "x is a fixed point of g" or that "g fixes x". For every x in X, the stabilizer subgroup of G with respect to x (also called the isotropy group or little group^[7]) is the set of all elements in G that fix x:

${\displaystyle G_x=\{g\in G\mid g\cdot x=x\}.}$

This is a subgroup of G, though typically not a normal one. The action of G on X is free if and only if all stabilizers are trivial. The kernel N of the homomorphism with the symmetric group, G → Sym(X), is given by the intersection of the stabilizers G_x for all x in X. If N is trivial, the action is said to be faithful (or effective).

Let x and y be two elements in X, and let g be a group element such that y = g⋅x. Then the two stabilizer groups G_x and G_y are related by G_y = g G_x g⁻¹. Proof: by definition, h ∈ G_y if and only if h⋅(g⋅x) = g⋅x. Applying g⁻¹ to both sides of this equality yields (g⁻¹hg)⋅x = x; that is, g⁻¹hg ∈ G_x. An opposite inclusion follows similarly by taking h ∈ G_x and supposing x = g⁻¹⋅y.

The above says that the stabilizers of elements in the same orbit are conjugate to each other. Thus, to each orbit, one can associate a conjugacy class of a subgroup of G (that is, the set of all conjugates of the subgroup). Let ${\displaystyle (H)}$ denote the conjugacy class of H. Then one says that the orbit O has type ${\displaystyle (H)}$ if the stabilizer ${\displaystyle G_x}$ of some/any x in O belongs to ${\displaystyle (H)}$. A maximal orbit type is often called a principal orbit type.

Orbits and stabilizers are closely related. For a fixed x in X, consider the map f:G → X given by g ↦ g·x. By definition the image f(G) of this map is the orbit G·x. The condition for two elements to have the same image is

${\displaystyle f(g)=f(h)⟺g\cdot x=h\cdot x⟺g^{-1}h\cdot x=x⟺g^{-1}h\in G_x⟺h\in g{G}_x}$.

In other words, g and h lie in the same coset for the stabilizer subgroup ${\displaystyle G_x}$. Thus the fibre ${\displaystyle f^{-1}(\{y\})}$ of f over any y in G·x is such a coset, and clearly every such coset occurs as a fibre. Therefore f defines a bijection between the set ${\displaystyle G/G_x}$ of cosets for the stabilizer subgroup and the orbit G·x, which sends ${\displaystyle g{G}_x\mapsto g\cdot x}$.^[8] This result is known as the orbit-stabilizer theorem.

If G is finite then the orbit-stabilizer theorem, together with Lagrange's theorem, gives

${\displaystyle |G\cdot x|=[G:G_x]=|G|/|G_x|,}$

in other words the length of the orbit of x times the order of its stabilizer is the order of the group. In particular that implies that the orbit length is a divisor of the group order.

Example: Let G be a group of prime order p acting on a set X with k elements. Since each orbit has either 1 or p elements, there are at least ${\displaystyle kmodp}$ orbits of length 1 which are G-invariant elements.

This result is especially useful since it can be employed for counting arguments (typically in situations where X is finite as well).

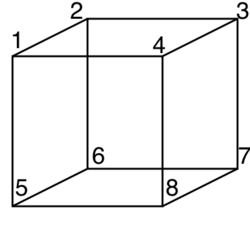
Example: One can use the orbit-stabilizer theorem to count the automorphisms of a graph. Consider the cubical graph as pictured, and let G denote its automorphism group. Then G acts on the set of vertices {1, 2, ..., 8}, and this action is transitive as can be seen by composing rotations about the center of the cube. Thus, by the orbit-stabilizer theorem, ${\displaystyle |G|=|G\cdot 1||G_1|=8|G_1|}$. Applying the theorem now to the stabilizer G₁, one can obtain ${\displaystyle |G_1|=|(G_1)\cdot 2||(G_1{)}_2|}$. Any element of G that fixes 1 must send 2 to either 2, 4, or 5. As an example of such automorphisms consider the rotation around the diagonal axis through 1 and 7 by ${\displaystyle 2\pi /3}$ which permutes 2,4,5 and 3,6,8, and fixes 1 and 7. Thus, ${\displaystyle |(G_1)\cdot 2|=3}$. Applying the theorem a third time gives ${\displaystyle |(G_1{)}_2|=|((G_1{)}_2)\cdot 3||((G_1{)}_2{)}_3|}$. Any element of G that fixes 1 and 2 must send 3 to either 3 or 6. Reflecting the cube at the plane through 1,2,7 and 8 is such an automorphism sending 3 to 6, thus ${\displaystyle |((G_1{)}_2)\cdot 3|=2}$. One also sees that ${\displaystyle ((G_1{)}_2{)}_3}$ consists only of the identity automorphism, as any element of G fixing 1, 2 and 3 must also fix all other vertices, since they are determined by their adjacency to 1, 2 and 3. Combining the preceding calculations, one can now obtain ${\displaystyle |G|=8\cdot 3\cdot 2\cdot 1=48}$.

A result closely related to the orbit-stabilizer theorem is Burnside's lemma:

${\displaystyle |X/G|=\frac{1}{|G|}\sum _{g\in G}|X^g|,}$

where X^g the set of points fixed by g. This result is mainly of use when G and X are finite, when it can be interpreted as follows: the number of orbits is equal to the average number of points fixed per group element.

Fixing a group G, the set of formal differences of finite G-sets forms a ring called the Burnside ring of G, where addition corresponds to disjoint union, and multiplication to Cartesian product.

• The trivial action of any group G on any set X is defined by g⋅x = x for all g in G and all x in X; that is, every group element induces the identity permutation on X.^[9]
• In every group G, left multiplication is an action of G on G: g⋅x = gx for all g, x in G. This action forms the basis of a rapid proof of Cayley's theorem - that every group is isomorphic to a subgroup of the symmetric group of permutations of the set G.
• In every group G with subgroup H, left multiplication is an action of G on the set of cosets G/H: g⋅aH = gaH for all g,a in G. In particular if H contains no nontrivial normal subgroups of G this induces an isomorphism from G to a subgroup of the permutation group of degree [G : H].
• In every group G, conjugation is an action of G on G: g⋅x = gxg⁻¹. An exponential notation is commonly used for the right-action variant: x^g = g⁻¹xg; it satisfies (x^g)^h = x^gh.
• In every group G with subgroup H, conjugation is an action of G on conjugates of H: g⋅K = gKg⁻¹ for all g in G and K conjugates of H.
• The symmetric group S_n and its subgroups act on the set { 1, …, n } by permuting its elements
• The symmetry group of a polyhedron acts on the set of vertices of that polyhedron. It also acts on the set of faces or the set of edges of the polyhedron.
• The symmetry group of any geometrical object acts on the set of points of that object.
• The automorphism group of a vector space (or graph, or group, or ring…) acts on the vector space (or set of vertices of the graph, or group, or ring…).
• The general linear group GL(n, K) and its subgroups, particularly its Lie subgroups (including the special linear group SL(n, K), orthogonal group O(n, K), special orthogonal group SO(n, K), and symplectic group Sp(n, K)) are Lie groups that act on the vector space Kⁿ. The group operations are given by multiplying the matrices from the groups with the vectors from Kⁿ.
• The general linear group GL(n, Z) acts on Zⁿ by natural matrix action. The orbits of its action are classified by the greatest common divisor of coordinates of the vector in Zⁿ.
• The affine group acts transitively on the points of an affine space, and the subgroup V of the affine group (that is, a vector space) transitive and free (that is, regular) action on these points;^[10] indeed this can be used to give a definition of an affine space.
• The projective linear group PGL(n + 1, K) and its subgroups, particularly its Lie subgroups, which are Lie groups that act on the projective space Pⁿ(K). This is a quotient of the action of the general linear group on projective space. Particularly notable is PGL(2, K), the symmetries of the projective line, which is sharply 3-transitive, preserving the cross ratio; the Möbius group PGL(2, C) is of particular interest.
• The isometries of the plane act on the set of 2D images and patterns, such as wallpaper patterns. The definition can be made more precise by specifying what is meant by image or pattern, for example, a function of position with values in a set of colors. Isometries are in fact one example of affine group (action).^{[dubious – discuss]}
• The sets acted on by a group G comprise the category of G-sets in which the objects are G-sets and the morphisms are G-set homomorphisms: functions f : X → Y such that g⋅(f(x)) = f(g⋅x) for every g in G.
• The Galois group of a field extension L/K acts on the field L but has only a trivial action on elements of the subfield K. Subgroups of Gal(L/K) correspond to subfields of L that contain K, that is, intermediate field extensions between L and K.
• The additive group of the real numbers (R, +) acts on the phase space of "well-behaved" systems in classical mechanics (and in more general dynamical systems) by time translation: if t is in R and x is in the phase space, then x describes a state of the system, and t + x is defined to be the state of the system t seconds later if t is positive or −t seconds ago if t is negative.
• The additive group of the real numbers (R, +) acts on the set of real functions of a real variable in various ways, with (t⋅f)(x) equal to, for example, f(x + t), f(x) + t, f(xe^t), f(x)e^t, f(x + t)e^t, or f(xe^t) + t, but not f(xe^t + t).
• Given a group action of G on X, we can define an induced action of G on the power set of X, by setting g⋅U = {g⋅u : u ∈ U} for every subset U of X and every g in G. This is useful, for instance, in studying the action of the large Mathieu group on a 24-set and in studying symmetry in certain models of finite geometries.
• The quaternions with norm 1 (the versors), as a multiplicative group, act on R³: for any such quaternion z = cos α/2 + v sin α/2, the mapping f(x) = zxz^∗ is a counterclockwise rotation through an angle α about an axis given by a unit vector v; z is the same rotation; see quaternions and spatial rotation. Note that this is not a faithful action because the quaternion −1 leaves all points where they were, as does the quaternion 1.

The notion of group action can be put in a broader context by using the action groupoid ${\displaystyle G^{\prime }=G⋉X}$ associated to the group action, thus allowing techniques from groupoid theory such as presentations and fibrations. Further the stabilizers of the action are the vertex groups, and the orbits of the action are the components, of the action groupoid. For more details, see the book Topology and groupoids referenced below.

This action groupoid comes with a morphism p: G′ → G which is a covering morphism of groupoids. This allows a relation between such morphisms and covering maps in topology.

If X and Y are two G-sets, a morphism from X to Y is a function f : X → Y such that f(g⋅x) = g⋅f(x) for all g in G and all x in X. Morphisms of G-sets are also called equivariant maps or G-maps.

The composition of two morphisms is again a morphism. If a morphism f is bijective, then its inverse is also a morphism. In this case f is called an isomorphism, and the two G-sets X and Y are called isomorphic; for all practical purposes, isomorphic G-sets are indistinguishable.

Some example isomorphisms:

• Every regular G action is isomorphic to the action of G on G given by left multiplication.
• Every free G action is isomorphic to G × S, where S is some set and G acts on G × S by left multiplication on the first coordinate. (S can be taken to be the set of orbits X/G.)
• Every transitive G action is isomorphic to left multiplication by G on the set of left cosets of some subgroup H of G. (H can be taken to be the stabilizer group of any element of the original G-set.)

With this notion of morphism, the collection of all G-sets forms a category; this category is a Grothendieck topos (in fact, assuming a classical metalogic, this topos will even be Boolean).

One often considers continuous group actions: the group G is a topological group, X is a topological space, and the map G × X → X is continuous with respect to the product topology of G × X. The space X is also called a G-space in this case. This is indeed a generalization, since every group can be considered a topological group by using the discrete topology. All the concepts introduced above still work in this context, however we define morphisms between G-spaces to be continuous maps compatible with the action of G. The quotient X/G inherits the quotient topology from X, and is called the quotient space of the action. The above statements about isomorphisms for regular, free and transitive actions are no longer valid for continuous group actions.

If X is a regular covering space of another topological space Y, then the action of the deck transformation group on X is properly discontinuous as well as being free. Every free, properly discontinuous action of a group G on a path-connected topological space X arises in this manner: the quotient map X ↦ X/G is a regular covering map, and the deck transformation group is the given action of G on X. Furthermore, if X is simply connected, the fundamental group of X/G will be isomorphic to G.

These results have been generalized in the book Topology and Groupoids referenced below to obtain the fundamental groupoid of the orbit space of a discontinuous action of a discrete group on a Hausdorff space, as, under reasonable local conditions, the orbit groupoid of the fundamental groupoid of the space. This allows calculations such as the fundamental group of the symmetric square of a space X, namely the orbit space of the product of X with itself under the twist action of the cyclic group of order 2 sending (x, y) to (y, x).

An action of a group G on a locally compact space X is cocompact if there exists a compact subset A of X such that GA = X. For a properly discontinuous action, cocompactness is equivalent to compactness of the quotient space X/G.

The action of G on X is said to be proper if the mapping G × X → X × X that sends (g, x) ↦ (g⋅x, x) is a proper map.

A group action of a topological group G on a topological space X is said to be strongly continuous if for all x in X, the map g ↦ g⋅x is continuous with respect to the respective topologies. Such an action induces an action on the space of continuous functions on X by defining (g⋅f)(x) = f(g⁻¹⋅x) for every g in G, f a continuous function on X, and x in X. Note that, while every continuous group action is strongly continuous, the converse is not in general true.^[11]

The subspace of smooth points for the action is the subspace of X of points x such that g ↦ g⋅x is smooth, that is, it is continuous and all derivatives^[where?] are continuous.

One can also consider actions of monoids on sets, by using the same two axioms as above. This does not define bijective maps and equivalence relations however. See semigroup action.

Instead of actions on sets, one can define actions of groups and monoids on objects of an arbitrary category: start with an object X of some category, and then define an action on X as a monoid homomorphism into the monoid of endomorphisms of X. If X has an underlying set, then all definitions and facts stated above can be carried over. For example, if we take the category of vector spaces, we obtain group representations in this fashion.

One can view a group G as a category with a single object in which every morphism is invertible. A (left) group action is then nothing but a (covariant) functor from G to the category of sets, and a group representation is a functor from G to the category of vector spaces. A morphism between G-sets is then a natural transformation between the group action functors. In analogy, an action of a groupoid is a functor from the groupoid to the category of sets or to some other category.

In addition to continuous actions of topological groups on topological spaces, one also often considers smooth actions of Lie groups on smooth manifolds, regular actions of algebraic groups on algebraic varieties, and actions of group schemes on schemes. All of these are examples of group objects acting on objects of their respective category.

• Measurable group action
• Gain graph
• Group with operators
• Monoid action

• Aschbacher, Michael (2000). Finite Group Theory. Cambridge University Press. ISBN 978-0-521-78675-1. 
• Brown, Ronald (2006). Topology and groupoids, Booksurge PLC, ISBN 1-4196-2722-8.
• Categories and groupoids, P.J. Higgins, downloadable reprint of van Nostrand Notes in Mathematics, 1971, which deal with applications of groupoids in group theory and topology.
• Dummit, David; Richard Foote (2004). Abstract Algebra (3rd ed.). Wiley. ISBN 0-471-43334-9. 
• Eie, Minking; Chang, Shou-Te (2010). A Course on Abstract Algebra. World Scientific. ISBN 978-981-4271-88-2. 
• Rotman, Joseph (1995). An Introduction to the Theory of Groups. Graduate Texts in Mathematics 148 (4th ed.). Springer-Verlag. ISBN 0-387-94285-8. 
• Smith, Jonathan D.H. (2008). Introduction to abstract algebra. Textbooks in mathematics. CRC Press. ISBN 978-1-4200-6371-4. 

• Hazewinkel, Michiel, ed. (2001), "Action of a group on a manifold", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=p/a010550 
• Weisstein, Eric W.. "Group Action". http://mathworld.wolfram.com/GroupAction.html. 

0.00 (0 votes)