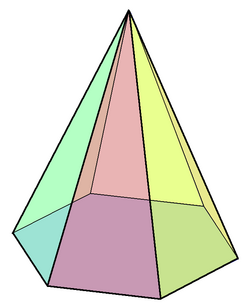
Hexagonal pyramid

Hexagonal pyramid
Type	Pyramid
Faces	6 triangles 1 hexagon
Edges	12
Vertices	7
Vertex configuration	6(32.6) (36)
Schläfli symbol	( ) ∨ {6}
Symmetry group	C6v, [6], (*66)
Rotation group	C6, [6]+, (66)
Dual polyhedron	Self-dual
Properties	Convex
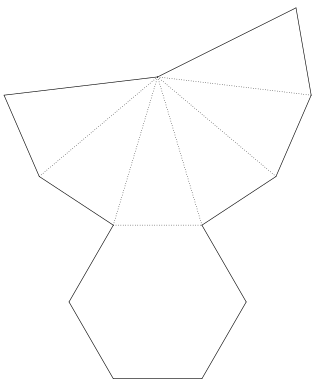
Net

In geometry, a hexagonal pyramid or hexacone is a pyramid with a hexagonal base upon which are erected six isosceles triangular faces that meet at a point (the apex). Like any pyramid, it is self-dual.

A right hexagonal pyramid with a regular hexagon base has C_6v symmetry.

A right regular pyramid is one which has a regular polygon as its base and whose apex is "above" the center of the base, so that the apex, the center of the base and any other vertex form a right triangle.

Vertex coordinates

A hexagonal pyramid of edge length 1 has the following vertices:

• [math]\displaystyle{ \left(\pm\frac12,\,\pm\frac{\sqrt3}{2},\,0\right) }[/math]
• [math]\displaystyle{ \left(\pm1,\,0,\,0\right) }[/math]
• [math]\displaystyle{ \left(0,\,0,\,0\right) }[/math]

These coordinates are a subset of the vertices of the regular triangular tiling.

Representations

A hexagonal pyramid has the following Coxeter diagrams:

• ox6oo&#x (full symmetry)
• ox3ox&#x (generally a ditrigonal pyramid)

Related polyhedra

See also

• Bipyramid, prism and antiprism

External links

• Weisstein, Eric W.. "Hexagonal Pyramid". http://mathworld.wolfram.com/HexagonalPyramid.html. 
• Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra
• Conway Notation for Polyhedra Try: "Y6"
• [1] Hexagonal pyramid - Polytope Wiki

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Hexagonal pyramid. Read more