Hilbert basis (linear programming)

The Hilbert basis of a convex cone C is a minimal set of integer vectors such that every integer vector in C is a conical combination of the vectors in the Hilbert basis with integer coefficients.

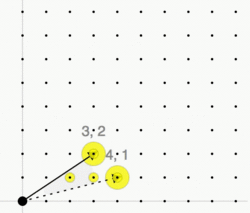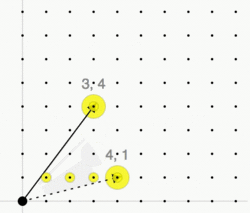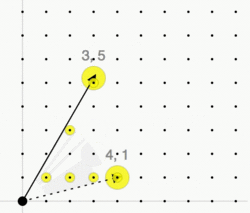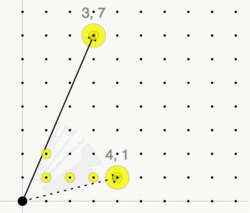
Given a lattice ${\displaystyle L\subset {\mathbb{\mathbb{Z}}}^d}$ and a convex polyhedral cone with generators ${\displaystyle a_1,\dots ,a_n\in {\mathbb{\mathbb{Z}}}^d}$

${\displaystyle C=\{{\lambda }_1{a}_1+\dots +{\lambda }_n{a}_n\mid {\lambda }_1,\dots ,{\lambda }_n\ge 0,{\lambda }_1,\dots ,{\lambda }_n\in \mathbb{ℝ}\}\subset {\mathbb{ℝ}}^d,}$

we consider the monoid ${\displaystyle C\cap L}$. By Gordan's lemma, this monoid is finitely generated, i.e., there exists a finite set of lattice points ${\displaystyle \{x_1,\dots ,x_m\}\subset C\cap L}$ such that every lattice point ${\displaystyle x\in C\cap L}$ is an integer conical combination of these points:

${\displaystyle x={\lambda }_1{x}_1+\dots +{\lambda }_m{x}_m,{\lambda }_1,\dots ,{\lambda }_m\in \mathbb{\mathbb{Z}},{\lambda }_1,\dots ,{\lambda }_m\ge 0.}$

The cone C is called pointed if ${\displaystyle x,-x\in C}$ implies ${\displaystyle x=0}$. In this case there exists a unique minimal generating set of the monoid ${\displaystyle C\cap L}$—the Hilbert basis of C. It is given by the set of irreducible lattice points: An element ${\displaystyle x\in C\cap L}$ is called irreducible if it can not be written as the sum of two non-zero elements, i.e., ${\displaystyle x=y+z}$ implies ${\displaystyle y=0}$ or ${\displaystyle z=0}$.

• Bruns, Winfried; Gubeladze, Joseph; Henk, Martin; Martin, Alexander; Weismantel, Robert (1999), "A counterexample to an integer analogue of Carathéodory's theorem", Journal für die reine und angewandte Mathematik 1999 (510): 179–185, doi:10.1515/crll.1999.045 
• Cook, William John; Fonlupt, Jean; Schrijver, Alexander (1986), "An integer analogue of Carathéodory's theorem", Journal of Combinatorial Theory, Series B 40 (1): 63–70, doi:10.1016/0095-8956(86)90064-X 
• Eisenbrand, Friedrich; Shmonin, Gennady (2006), "Carathéodory bounds for integer cones", Operations Research Letters 34 (5): 564–568, doi:10.1016/j.orl.2005.09.008, http://infoscience.epfl.ch/record/121640 
• D. V. Pasechnik (2001). "On computing the Hilbert bases via the Elliott—MacMahon algorithm". Theoretical Computer Science 263 (1–2): 37–46. doi:10.1016/S0304-3975(00)00229-2. 

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Hilbert basis (linear programming). Read more