J-invariant

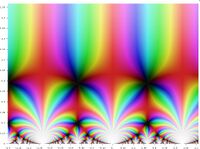
In mathematics, Felix Klein's j-invariant or j function, regarded as a function of a complex variable τ, is a modular function of weight zero for SL(2, Z) defined on the upper half-plane of complex numbers. It is the unique such function which is holomorphic away from a simple pole at the cusp such that

[math]\displaystyle{ j\left(e^{2\pi i/3}\right) = 0, \quad j(i) = 1728 = 12^3. }[/math]

Rational functions of j are modular, and in fact give all modular functions. Classically, the j-invariant was studied as a parameterization of elliptic curves over [math]\displaystyle{ \mathbb{C} }[/math], but it also has surprising connections to the symmetries of the Monster group (this connection is referred to as monstrous moonshine).

Definition

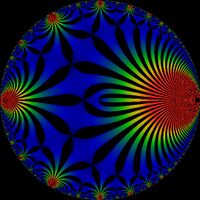
The j-invariant can be defined as a function on the upper half-plane H = {τ ∈ C, Im(τ) > 0},

[math]\displaystyle{ j(\tau) = 1728 \frac{g_2(\tau)^3}{\Delta(\tau)} = 1728 \frac{g_2(\tau)^3}{g_2(\tau)^3 - 27g_3(\tau)^2} = 1728 \frac{g_2(\tau)^3}{(2\pi)^{12}\,\eta^{24}(\tau)} }[/math]

with the third definition implying [math]\displaystyle{ j(\tau) }[/math] can be expressed as a cube, also since 1728[math]\displaystyle{ {} = 12^3 }[/math].

The given functions are the modular discriminant [math]\displaystyle{ \Delta(\tau) = g_2(\tau)^3 - 27g_3(\tau)^2 = (2\pi)^{12}\,\eta^{24}(\tau) }[/math], Dedekind eta function [math]\displaystyle{ \eta(\tau) }[/math], and modular invariants,

[math]\displaystyle{ g_2(\tau) = 60G_4(\tau) = 60\sum_{(m,n) \neq (0,0)} \left(m + n\tau\right)^{-4} }[/math]

[math]\displaystyle{ g_3(\tau) = 140G_6(\tau) = 140\sum_{(m,n) \neq (0,0)} \left(m + n\tau\right)^{-6} }[/math]

where [math]\displaystyle{ G_4(\tau) }[/math], [math]\displaystyle{ G_6(\tau) }[/math] are Fourier series,

[math]\displaystyle{ \begin{align} G_4(\tau)&=\frac{\pi^4}{45}\, E_4(\tau) \\[4pt] G_6(\tau)&=\frac{2\pi^6}{945}\, E_6(\tau) \end{align} }[/math]

and [math]\displaystyle{ E_4(\tau) }[/math], [math]\displaystyle{ E_6(\tau) }[/math] are Eisenstein series,

[math]\displaystyle{ \begin{align} E_4(\tau)&= 1+ 240\sum_{n=1}^\infty \frac{n^3 q^n}{1-q^n} \\[4pt] E_6(\tau)&= 1- 504\sum_{n=1}^\infty \frac{n^5 q^n}{1-q^n} \end{align} }[/math]

and [math]\displaystyle{ q=e^{2\pi i \tau} }[/math] (the square of the nome). The j-invariant can then be directly expressed in terms of the Eisenstein series as,

[math]\displaystyle{ j(\tau) = 1728 \frac{E_4(\tau)^3}{E_4(\tau)^3 - E_6(\tau)^2} }[/math]

with no numerical factor other than 1728. This implies a third way to define the modular discriminant,^[1]

[math]\displaystyle{ \Delta(\tau) = (2\pi)^{12}\,\frac{E_4(\tau)^3 - E_6(\tau)^2}{1728} }[/math]

For example, using the definitions above and [math]\displaystyle{ \tau = 2i }[/math], then the Dedekind eta function [math]\displaystyle{ \eta(2i) }[/math] has the exact value,

[math]\displaystyle{ \eta(2i) = \frac{\Gamma \left(\frac14\right)}{2^{11/8} \pi^{3/4}} }[/math]

implying the transcendental numbers,

[math]\displaystyle{ g_2(2i) = \frac{11\,\Gamma \left(\frac14\right)^8}{2^{8} \pi^2},\qquad g_3(2i) = \frac{7\,\Gamma \left(\frac14\right)^{12}}{2^{12} \pi^3} }[/math]

but yielding the algebraic number (in fact, an integer),

[math]\displaystyle{ j(2i) = 1728 \frac{g_2(2i)^3}{g_2(2i)^3 - 27g_3(2i)^2} = 66^3. }[/math]

In general, this can be motivated by viewing each τ as representing an isomorphism class of elliptic curves. Every elliptic curve E over C is a complex torus, and thus can be identified with a rank 2 lattice; that is, a two-dimensional lattice of C. This lattice can be rotated and scaled (operations that preserve the isomorphism class), so that it is generated by 1 and τ ∈ H. This lattice corresponds to the elliptic curve [math]\displaystyle{ y^2=4x^3-g_2(\tau)x-g_3(\tau) }[/math] (see Weierstrass elliptic functions).

Note that j is defined everywhere in H as the modular discriminant is non-zero. This is due to the corresponding cubic polynomial having distinct roots.

The fundamental region

It can be shown that Δ is a modular form of weight twelve, and g₂ one of weight four, so that its third power is also of weight twelve. Thus their quotient, and therefore j, is a modular function of weight zero, in particular a holomorphic function H → C invariant under the action of SL(2, Z). Quotienting out by its centre { ±I } yields the modular group, which we may identify with the projective special linear group PSL(2, Z).

By a suitable choice of transformation belonging to this group,

[math]\displaystyle{ \tau \mapsto \frac{a\tau + b}{c\tau +d}, \qquad ad-bc =1, }[/math]

we may reduce τ to a value giving the same value for j, and lying in the fundamental region for j, which consists of values for τ satisfying the conditions

[math]\displaystyle{ \begin{align} |\tau| &\ge 1 \\[5pt] -\tfrac{1}{2} &\lt \mathfrak{R}(\tau) \le \tfrac{1}{2} \\[5pt] -\tfrac{1}{2} &\lt \mathfrak{R}(\tau) \lt 0 \Rightarrow |\tau| \gt 1 \end{align} }[/math]

The function j(τ) when restricted to this region still takes on every value in the complex numbers C exactly once. In other words, for every c in C, there is a unique τ in the fundamental region such that c = j(τ). Thus, j has the property of mapping the fundamental region to the entire complex plane.

Additionally two values τ,τ' ∈H produce the same elliptic curve iff τ = T(τ') for some T ∈ PSL(2, Z). This means j provides a bijection from the set of elliptic curves over C to the complex plane.^[2]

As a Riemann surface, the fundamental region has genus 0, and every (level one) modular function is a rational function in j; and, conversely, every rational function in j is a modular function. In other words, the field of modular functions is C(j).

Class field theory and j

The j-invariant has many remarkable properties:

• If τ is any point of the upper half plane whose corresponding elliptic curve has complex multiplication (that is, if τ is any element of an imaginary quadratic field with positive imaginary part, so that j is defined), then j(τ) is an algebraic integer.^[3] These special values are called singular moduli.
• The field extension Q[j(τ), τ]/Q(τ) is abelian, that is, it has an abelian Galois group.
• Let Λ be the lattice in C generated by {1, τ}. It is easy to see that all of the elements of Q(τ) which fix Λ under multiplication form a ring with units, called an order. The other lattices with generators {1, τ′}, associated in like manner to the same order define the algebraic conjugates j(τ′) of j(τ) over Q(τ). Ordered by inclusion, the unique maximal order in Q(τ) is the ring of algebraic integers of Q(τ), and values of τ having it as its associated order lead to unramified extensions of Q(τ).

These classical results are the starting point for the theory of complex multiplication.

Transcendence properties

In 1937 Theodor Schneider proved the aforementioned result that if τ is a quadratic irrational number in the upper half plane then j(τ) is an algebraic integer. In addition he proved that if τ is an algebraic number but not imaginary quadratic then j(τ) is transcendental.

The j function has numerous other transcendental properties. Kurt Mahler conjectured a particular transcendence result that is often referred to as Mahler's conjecture, though it was proved as a corollary of results by Yu. V. Nesterenko and Patrice Phillipon in the 1990s. Mahler's conjecture was that if τ was in the upper half plane then e^2πiτ and j(τ) were never both simultaneously algebraic. Stronger results are now known, for example if e^2πiτ is algebraic then the following three numbers are algebraically independent, and thus at least two of them transcendental:

[math]\displaystyle{ j(\tau), \frac{j^\prime(\tau)}{\pi}, \frac{j^{\prime\prime}(\tau)}{\pi^2} }[/math]

The q-expansion and moonshine

Several remarkable properties of j have to do with its q-expansion (Fourier series expansion), written as a Laurent series in terms of q = e^2πiτ, which begins:

[math]\displaystyle{ j(\tau) = q^{-1} + 744 + 196884 q + 21493760 q^2 + 864299970 q^3 + 20245856256 q^4 + \cdots }[/math]

Note that j has a simple pole at the cusp, so its q-expansion has no terms below q⁻¹.

All the Fourier coefficients are integers, which results in several almost integers, notably Ramanujan's constant:

[math]\displaystyle{ e^{\pi \sqrt{163}} \approx 640320^3 + 744 }[/math].

The asymptotic formula for the coefficient of qⁿ is given by

[math]\displaystyle{ \frac{e^{4\pi\sqrt{n}}}{\sqrt{2}\,n^{3/4}} }[/math],

as can be proved by the Hardy–Littlewood circle method.^[4][5]

Moonshine

More remarkably, the Fourier coefficients for the positive exponents of q are the dimensions of the graded part of an infinite-dimensional graded algebra representation of the monster group called the moonshine module – specifically, the coefficient of qⁿ is the dimension of grade-n part of the moonshine module, the first example being the Griess algebra, which has dimension 196,884, corresponding to the term 196884q. This startling observation, first made by John McKay, was the starting point for moonshine theory.

The study of the Moonshine conjecture led John Horton Conway and Simon P. Norton to look at the genus-zero modular functions. If they are normalized to have the form

[math]\displaystyle{ q^{-1} + {O}(q) }[/math]

then John G. Thompson showed that there are only a finite number of such functions (of some finite level), and Chris J. Cummins later showed that there are exactly 6486 of them, 616 of which have integral coefficients.^[6]

Alternate expressions

We have

[math]\displaystyle{ j(\tau) = \frac{256\left(1-x\right)^3}{x^2} }[/math]

where x = λ(1 − λ) and λ is the modular lambda function

[math]\displaystyle{ \lambda(\tau) = \frac{\theta_2^4(e^{\pi i\tau})}{\theta_3^4(e^{\pi i\tau})} = k^2(\tau) }[/math]

a ratio of Jacobi theta functions θ_m, and is the square of the elliptic modulus k(τ).^[7] The value of j is unchanged when λ is replaced by any of the six values of the cross-ratio:^[8]

[math]\displaystyle{ \left\lbrace { \lambda, \frac{1}{1-\lambda}, \frac{\lambda-1}{\lambda}, \frac{1}{\lambda}, \frac{\lambda}{\lambda-1}, 1-\lambda } \right\rbrace }[/math]

The branch points of j are at {0, 1, ∞}, so that j is a Belyi function.^[9]

Expressions in terms of theta functions

Define the nome q = e^πiτ and the Jacobi theta function,

[math]\displaystyle{ \vartheta(0; \tau) = \vartheta_{00}(0; \tau) = 1 + 2 \sum_{n=1}^\infty \left(e^{\pi i\tau}\right)^{n^2} = \sum_{n=-\infty}^\infty q^{n^2} }[/math]

from which one can derive the auxiliary theta functions, defined here. Let,

[math]\displaystyle{ \begin{align} a &= \theta_{2}(q) = \vartheta_{10}(0; \tau) \\ b &= \theta_{3}(q) = \vartheta_{00}(0; \tau) \\ c &= \theta_{4}(q) = \vartheta_{01}(0; \tau) \end{align} }[/math]

where ϑ_ij and θ_n are alternative notations, and a⁴ − b⁴ + c⁴ = 0. Then we have the for modular invariants g₂, g₃,

[math]\displaystyle{ \begin{align} g_2(\tau) &= \tfrac{2}{3}\pi^4 \left(a^8 + b^8 + c^8\right) \\ g_3(\tau) &= \tfrac{4}{27}\pi^6 \sqrt{\frac{\left(a^8+b^8+c^8\right)^3-54\left(abc\right)^8}{2}} \\ \end{align} }[/math]

and modular discriminant,

[math]\displaystyle{ \Delta = g_2^3-27g_3^2 = (2\pi)^{12} \left(\tfrac{1}{2}a b c\right)^8 = (2\pi)^{12}\eta(\tau)^{24} }[/math]

with Dedekind eta function η(τ). The j(τ) can then be rapidly computed,

[math]\displaystyle{ j(\tau) = 1728\frac{g_2^3}{g_2^3-27g_3^2} = 32 \frac{\left(a^8 + b^8 + c^8\right)^3 }{ \left(a b c\right)^8} }[/math]

Algebraic definition

So far we have been considering j as a function of a complex variable. However, as an invariant for isomorphism classes of elliptic curves, it can be defined purely algebraically.^[10] Let

[math]\displaystyle{ y^2 + a_1 xy + a_3 y = x^3 + a_2 x^2 + a_4 x + a_6 }[/math]

be a plane elliptic curve over any field. Then we may perform successive transformations to get the above equation into the standard form y² = 4x³ − g₂x − g₃ (note that this transformation can only be made when the characteristic of the field is not equal to 2 or 3). The resulting coefficients are:

[math]\displaystyle{ \begin{align} b_2 &= a_1^2 + 4a_2,\quad &b_4 &= a_1a_3 + 2a_4,\\ b_6 &= a_3^2 + 4a_6,\quad &b_8 &= a_1^2a_6 - a_1a_3a_4 + a_2a_3^2 + 4a_2a_6 - a_4^2,\\ c_4 &= b_2^2 - 24b_4,\quad &c_6 &= -b_2^3 + 36b_2b_4 - 216b_6, \end{align} }[/math]

where g₂ = c₄ and g₃ = c₆. We also have the discriminant

[math]\displaystyle{ \Delta = -b_2^2b_8 + 9b_2b_4b_6 - 8b_4^3 - 27b_6^2. }[/math]

The j-invariant for the elliptic curve may now be defined as

[math]\displaystyle{ j = \frac{c_4^3}{\Delta} }[/math]

In the case that the field over which the curve is defined has characteristic different from 2 or 3, this is equal to

[math]\displaystyle{ j = 1728\frac{c_4^3}{c_4^3-c_6^2}. }[/math]

Inverse function

The inverse function of the j-invariant can be expressed in terms of the hypergeometric function ₂F₁ (see also the article Picard–Fuchs equation). Explicitly, given a number N, to solve the equation j(τ) = N for τ can be done in at least four ways.

Method 1: Solving the sextic in λ,

[math]\displaystyle{ j(\tau) = \frac{256\bigl(1-\lambda(1-\lambda)\bigr)^3}{\bigl(\lambda(1-\lambda)\bigr)^2} = \frac{256\left(1-x\right)^3}{x^2} }[/math]

where x = λ(1 − λ), and λ is the modular lambda function so the sextic can be solved as a cubic in x. Then,

[math]\displaystyle{ \tau = i \ \frac{{}_2F_1 \left (\tfrac{1}{2},\tfrac{1}{2},1;1 - \lambda \right )}{{}_2F_1 \left (\tfrac{1}{2},\tfrac{1}{2},1;\lambda \right)}=i\frac{\operatorname{M}(1,\sqrt{1-\lambda})}{\operatorname{M}(1,\sqrt{\lambda})} }[/math]

for any of the six values of λ, where M is the arithmetic–geometric mean.^{[note 1]}

Method 2: Solving the quartic in γ,

[math]\displaystyle{ j(\tau) = \frac{27\left(1 + 8\gamma\right)^3}{\gamma\left(1 - \gamma\right)^3} }[/math]

then for any of the four roots,

[math]\displaystyle{ \tau = \frac{i}{\sqrt{3}} \frac{{}_2F_1 \left (\tfrac{1}{3},\tfrac{2}{3},1;1-\gamma \right)}{{}_2F_1 \left(\tfrac{1}{3},\tfrac{2}{3},1;\gamma \right )} }[/math]

Method 3: Solving the cubic in β,

[math]\displaystyle{ j(\tau) = \frac{64\left(1+3\beta\right)^3}{\beta\left(1-\beta\right)^2} }[/math]

then for any of the three roots,

[math]\displaystyle{ \tau = \frac{i}{\sqrt{2}} \frac{{}_2F_1 \left (\tfrac{1}{4},\tfrac{3}{4},1;1-\beta \right)}{{}_2F_1 \left(\tfrac{1}{4},\tfrac{3}{4},1;\beta \right )} }[/math]

Method 4: Solving the quadratic in α,

[math]\displaystyle{ j(\tau)=\frac{1728}{4\alpha(1-\alpha)} }[/math]

then,

[math]\displaystyle{ \tau = i \ \frac{{}_2F_1 \left (\tfrac{1}{6},\tfrac{5}{6},1;1-\alpha \right)}{{}_2F_1 \left(\tfrac{1}{6},\tfrac{5}{6},1;\alpha \right )} }[/math]

One root gives τ, and the other gives −1/τ, but since j(τ) = j(−1/τ), it makes no difference which α is chosen. The latter three methods can be found in Ramanujan's theory of elliptic functions to alternative bases.

The inversion is applied in high-precision calculations of elliptic function periods even as their ratios become unbounded.^{[citation needed]} A related result is the expressibility via quadratic radicals of the values of j at the points of the imaginary axis whose magnitudes are powers of 2 (thus permitting compass and straightedge constructions). The latter result is hardly evident since the modular equation for j of order 2 is cubic.^[11]

Pi formulas

The Chudnovsky brothers found in 1987,^[12]

[math]\displaystyle{ \frac{1}{\pi} = \frac{12}{640320^{3/2}} \sum_{k=0}^\infty \frac{(6k)! (163 \cdot 3344418k + 13591409)}{(3k)!\left(k!\right)^3 \left(-640320\right)^{3k}} }[/math]

a proof of which uses the fact that

[math]\displaystyle{ j\left(\frac{1+\sqrt{-163}}{2}\right) = -640320^3. }[/math]

For similar formulas, see the Ramanujan–Sato series.

Special values

The j-invariant vanishes at the "corner" of the fundamental domain:

[math]\displaystyle{ \quad j\!\left( \tfrac{1 + \sqrt{3}i}{2} \right) = 0. }[/math]

Here are a few more special values^{[citation needed]} given in terms of the alternative notation J(τ) ≡ 1/1728 j(τ), the first five well known:

[math]\displaystyle{ \begin{align} J(i) &= J \left( \tfrac{1 + i}{2} \right) = 1 \\ J\left(\sqrt{2}i\right) &= \left(\tfrac{5}{3}\right)^3 \\ J(2i) &= \left(\tfrac{11}{2}\right)^3 \\ J\left(2\sqrt{2}i\right) &= \tfrac{125}{216} \left(19 + 13\sqrt{2} \right)^3\\ J\left(\tfrac{1+\sqrt{163}i}{2}\right) &=-53360^3\\ J(4i) &= \tfrac{1}{64} \left(724 + 513\sqrt{2} \right)^3\\ J\left( \tfrac{1 + 2i}{2} \right) &= \tfrac{1}{64} \left(724 - 513\sqrt{2} \right)^3\\ J\left( \tfrac{1 + 2\sqrt{2}i}{3} \right) &= \tfrac{125}{216} \left(19 - 13\sqrt{2} \right)^3\\ J(3i) &= \tfrac{1}{27} \left(2 + \sqrt{3}\right)^2 \left(21 + 20\sqrt{3}\right )^3 \\ J\left(2\sqrt{3}i\right) &= \tfrac{125}{16} \left(30 + 17\sqrt{3}\right)^3\\ J\left( \tfrac{1 + 7\sqrt{3}i}{2} \right) &= -\tfrac{64000}{7} \left(651 + 142\sqrt{21} \right)^3\\ J\left(\tfrac{1 + 3\sqrt{11}i}{10} \right) &= \tfrac{64}{27} \left(23 - 4\sqrt{33}\right)^2 \left(-77 + 15\sqrt{33} \right)^3\\ J\left(\sqrt{21}i\right) &= \tfrac{1}{128} \left(3 + \sqrt{7} \right)^5 \left( 17 + 7\sqrt{3} + 59\sqrt{7} + 35\sqrt{21}\right)^3\\ J\left( \tfrac{\sqrt{30}i}{1} \right) &= \tfrac{1}{4} \left(7 + 5\sqrt{2} + 3\sqrt{5} + 2\sqrt{10} \right)^4 \left( 55 + 30\sqrt{2} + 12\sqrt{5} + 10\sqrt{10} \right)^3\\ J\left( \tfrac{\sqrt{30}i}{2} \right) &= \tfrac{1}{4} \left(7 + 5\sqrt{2} - 3\sqrt{5} - 2\sqrt{10} \right)^4 \left( 55 + 30\sqrt{2} - 12\sqrt{5} - 10\sqrt{10} \right)^3\\ J\left( \tfrac{\sqrt{30}i}{5} \right) &= \tfrac{1}{4} \left(7 - 5\sqrt{2} + 3\sqrt{5} - 2\sqrt{10} \right)^4 \left( 55 - 30\sqrt{2} + 12\sqrt{5} - 10\sqrt{10} \right)^3\\ J\left( \tfrac{\sqrt{30}i}{10} \right) &= \tfrac{1}{4} \left(7 - 5\sqrt{2} - 3\sqrt{5} + 2\sqrt{10} \right)^4 \left( 55 - 30\sqrt{2} - 12\sqrt{5} + 10\sqrt{10} \right)^3\\ J\left(\tfrac{1+\sqrt{31}i}{2}\right) &= \left(1 - \frac1{64} \left[ (13 + \sqrt{93})\sqrt[3]{ 4(29-3\sqrt{93}) } + (13 - \sqrt{93}) \sqrt[3]{ 4(29+3\sqrt{93}) }+8\right]^2\right)^3\\ J(\sqrt{70}i) &= \left(1 + \tfrac{9}{4}\left(303 + 220\sqrt{2} + 139\sqrt{5} + 96\sqrt{10}\right)^2 \right)^3 \\ J(7i) &= \left( 1 + \tfrac{9}{32} \sqrt[4]{28} \left(3 + \sqrt{7} \right)^3 \left(13 + 3\sqrt{7} + \left(6 + \sqrt{7} \right)\sqrt[4]{28}\right)^2 \right)^3\\ J(8i) &= \left( 1 + \tfrac{9}{4} \sqrt[4]{2} \left (1 + \sqrt{2} \right) \left(123 + 104\sqrt[4]{2} + 88\sqrt{2} + 73\sqrt[4]{8}\right)^2 \right)^3\\ J(10i) &= \left(1 + \tfrac{9}{8}\left(2402 + 1607\sqrt[4]{5} + 1074\sqrt[4]{25} + 719\sqrt[4]{125}\right)^2 \right)^3\\ J \left( \tfrac{5i}{2} \right) &= \left(1 + \tfrac{9}{8}\left(2402 - 1607\sqrt[4]{5} + 1074\sqrt[4]{25} - 719\sqrt[4]{125}\right)^2 \right)^3\\ J(2\sqrt{58}i) &= \left(1+\tfrac{9}{256}\left(1+\sqrt{2}\right)^5\left(5+\sqrt{29}\right)^5\left(793+907\sqrt{2}+237\sqrt{29}+103\sqrt{58}\right)^2\right)^3\\ J\left( \tfrac{1 + \sqrt{1435}i}{2} \right) &= \left( 1 - 9 \left ( 9892538 + 4424079\sqrt{5} + 1544955\sqrt{41} + 690925\sqrt{205} \right )^2 \right)^3\\ J\left( \tfrac{1 + \sqrt{1555}i}{2} \right) &= \left( 1 - 9 \left ( 22297077 + 9971556\sqrt{5} + \left ( 3571365 + 1597163\sqrt{5} \right ) \sqrt{\tfrac{31 + 21\sqrt{5}}{2}} \right)^2 \right)^3\\ \end{align} }[/math]

Failure to classify elliptic curves over other fields

The [math]\displaystyle{ j }[/math]-invariant is only sensitive to isomorphism classes of elliptic curves over the complex numbers, or more generally, an algebraically closed field. Over other fields there exist examples of elliptic curves whose [math]\displaystyle{ j }[/math]-invariant is the same, but are non-isomorphic. For example, let [math]\displaystyle{ E_1,E_2 }[/math] be the elliptic curves associated to the polynomials

[math]\displaystyle{ \begin{align} E_1: &\text{ } y^2 = x^3 - 25x \\ E_2: &\text{ } y^2 = x^3 - 4x, \end{align} }[/math]

both having [math]\displaystyle{ j }[/math]-invariant [math]\displaystyle{ 1728 }[/math]. Then, the rational points of [math]\displaystyle{ E_2 }[/math] can be computed as:

[math]\displaystyle{ E_2(\mathbb{Q}) = \{\infty, (2,0), (-2,0), (0,0) \} }[/math]

since [math]\displaystyle{ x^3 - 4x = x(x^2 - 4) = x(x-2)(x+2). }[/math] There are no rational solutions with [math]\displaystyle{ y = a \neq 0 }[/math]. This can be shown using Cardano's formula to show that in that case the solutions to [math]\displaystyle{ x^3 - 4x - a^2 }[/math] are all irrational. On the other hand, on the set of points

[math]\displaystyle{ \{ n(-4,6) : n \in \mathbb{Z} \} }[/math]

the equation for [math]\displaystyle{ E_1 }[/math] becomes [math]\displaystyle{ 36n^2 = -64n^3 + 100n }[/math]. Dividing by [math]\displaystyle{ 4n }[/math] to eliminate the [math]\displaystyle{ (0,0) }[/math] solution, the quadratic formula gives the rational solutions:

[math]\displaystyle{ n = \frac{ -9 \pm \sqrt{81 - 4\cdot 16\cdot(-25)} }{2\cdot 16} = \frac{-9 \pm 41}{32}. }[/math]

If these curves are considered over [math]\displaystyle{ \mathbb{Q}(\sqrt{10}) }[/math], there is an isomorphism [math]\displaystyle{ E_1(\mathbb{Q}(\sqrt{10})) \cong E_2(\mathbb{Q}(\sqrt{10})) }[/math] sending

[math]\displaystyle{ (x,y)\mapsto (\mu^2x,\mu^3y) \ \text{ where }\ \mu = \frac{\sqrt{10}}{2}. }[/math]

References

Notes

Other

• Apostol, Tom M. (1976), Modular functions and Dirichlet Series in Number Theory, Graduate Texts in Mathematics, 41, New York: Springer-Verlag . Provides a very readable introduction and various interesting identities.
  • Apostol, Tom M. (1990), Modular functions and Dirichlet Series in Number Theory, Graduate Texts in Mathematics, 41 (2nd ed.), doi:10.1007/978-1-4612-0999-7, ISBN 978-0-387-97127-8, https://archive.org/details/modularfunctions0000apos 
• Berndt, Bruce C.; Chan, Heng Huat (1999), "Ramanujan and the modular j-invariant", Canadian Mathematical Bulletin 42 (4): 427–440, doi:10.4153/CMB-1999-050-1 . Provides a variety of interesting algebraic identities, including the inverse as a hypergeometric series.
• Cox, David A. (1989), Primes of the Form x^2 + ny^2: Fermat, Class Field Theory, and Complex Multiplication, New York: Wiley-Interscience Publication, John Wiley & Sons Inc.  Introduces the j-invariant and discusses the related class field theory.
• Conway, John Horton; Norton, Simon (1979), "Monstrous moonshine", Bulletin of the London Mathematical Society 11 (3): 308–339, doi:10.1112/blms/11.3.308 . Includes a list of the 175 genus-zero modular functions.
• Rankin, Robert A. (1977), Modular forms and functions, Cambridge: Cambridge University Press, ISBN 978-0-521-21212-0 . Provides a short review in the context of modular forms.
• Schneider, Theodor (1937), "Arithmetische Untersuchungen elliptischer Integrale", Math. Annalen 113: 1–13, doi:10.1007/BF01571618 .

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/J-invariant. Read more