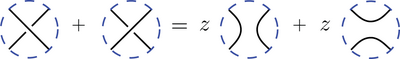Kauffman polynomial

In knot theory, the Kauffman polynomial is a 2-variable knot polynomial due to Louis Kauffman.^[1] It is initially defined on a link diagram as

[math]\displaystyle{ F(K)(a,z)=a^{-w(K)}L(K)\, }[/math],

where [math]\displaystyle{ w(K) }[/math] is the writhe of the link diagram and [math]\displaystyle{ L(K) }[/math] is a polynomial in a and z defined on link diagrams by the following properties:

• [math]\displaystyle{ L(O) = 1 }[/math] (O is the unknot).
• [math]\displaystyle{ L(s_r)=aL(s), \qquad L(s_\ell)=a^{-1}L(s). }[/math]
• L is unchanged under type II and III Reidemeister moves.

Here [math]\displaystyle{ s }[/math] is a strand and [math]\displaystyle{ s_r }[/math] (resp. [math]\displaystyle{ s_\ell }[/math]) is the same strand with a right-handed (resp. left-handed) curl added (using a type I Reidemeister move).

Additionally L must satisfy Kauffman's skein relation:

The pictures represent the L polynomial of the diagrams which differ inside a disc as shown but are identical outside.

Kauffman showed that L exists and is a regular isotopy invariant of unoriented links. It follows easily that F is an ambient isotopy invariant of oriented links.

The Jones polynomial is a special case of the Kauffman polynomial, as the L polynomial specializes to the bracket polynomial. The Kauffman polynomial is related to Chern–Simons gauge theories for SO(N) in the same way that the HOMFLY polynomial is related to Chern–Simons gauge theories for SU(N).^[2]

References

Further reading

• Kauffman, Louis (1987). On Knots. Annals of Mathematics Studies. 115. Princeton, NJ: Princeton University Press. ISBN 0-691-08435-1. 

External links

• "Kauffman polynomial", Encyclopedia of Mathematics
• "The Kauffman Polynomial", The Knot Atlas.

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Kauffman polynomial. Read more