Lax–Friedrichs method

The Lax–Friedrichs method, named after Peter Lax and Kurt O. Friedrichs, is a numerical method for the solution of hyperbolic partial differential equations based on finite differences. The method can be described as the FTCS (forward in time, centered in space) scheme with a numerical dissipation term of 1/2. One can view the Lax–Friedrichs method as an alternative to Godunov's scheme, where one avoids solving a Riemann problem at each cell interface, at the expense of adding artificial viscosity.

Illustration for a Linear Problem

Consider a one-dimensional, linear hyperbolic partial differential equation for [math]\displaystyle{ u(x,t) }[/math] of the form: [math]\displaystyle{ u_t + a u_x = 0 }[/math] on the domain [math]\displaystyle{ b \leq x \leq c,\; 0 \leq t \leq d }[/math] with initial condition [math]\displaystyle{ u(x,0) = u_0(x)\, }[/math] and the boundary conditions [math]\displaystyle{ \begin{align} u(b,t) &= u_b(t) \\ u(c,t) &= u_c(t). \end{align} }[/math]

If one discretizes the domain [math]\displaystyle{ (b, c) \times (0, d) }[/math] to a grid with equally spaced points with a spacing of [math]\displaystyle{ \Delta x }[/math] in the [math]\displaystyle{ x }[/math]-direction and [math]\displaystyle{ \Delta t }[/math] in the [math]\displaystyle{ t }[/math]-direction, we introduce an approximation [math]\displaystyle{ \tilde u }[/math] of [math]\displaystyle{ u }[/math] [math]\displaystyle{ u_i^n = \tilde u(x_i, t^n) ~~\text{ with }~~ \begin{array}{l}x_i = b + i\,\Delta x ,\\ t^n = n\,\Delta t\end{array} ~~\text{ for }~~ \begin{array}{l}i = 0,\ldots,N ,\\ n = 0,\ldots,M,\end{array} }[/math] where [math]\displaystyle{ N = \frac{c - b}{\Delta x} ,\, M = \frac{d}{\Delta t} }[/math] are integers representing the number of grid intervals. Then the Lax–Friedrichs method to approximate the partial differential equation is given by: [math]\displaystyle{ \frac{u_i^{n+1} - \frac{1}{2}(u_{i+1}^n + u_{i-1}^n)}{\Delta t} + a\frac{u_{i+1}^n - u_{i-1}^n}{2\,\Delta x} = 0 }[/math]

Or, rewriting this to solve for the unknown [math]\displaystyle{ u_i^{n+1}, }[/math] [math]\displaystyle{ u_i^{n+1} = \frac{1}{2} \left(u_{i+1}^n + u_{i-1}^n\right) - a\frac{\Delta t}{2\,\Delta x} \left(u_{i+1}^n - u_{i-1}^n\right) }[/math]

Where the initial values and boundary nodes are taken from [math]\displaystyle{ \begin{align} u_i^0 &= u_0(x_i) \\ u_0^n &= u_b(t^n) \\ u_N^n &= u_c(t^n). \end{align} }[/math]

Extensions to Nonlinear Problems

A nonlinear hyperbolic conservation law is defined through a flux function [math]\displaystyle{ f }[/math]: [math]\displaystyle{ u_t + ( f(u) )_x = 0. }[/math]

In the case of [math]\displaystyle{ f(u) = a u }[/math], we end up with a scalar linear problem. Note that in general, [math]\displaystyle{ u }[/math] is a vector with [math]\displaystyle{ m }[/math] equations in it. The generalization of the Lax-Friedrichs method to nonlinear systems takes the form^[1] [math]\displaystyle{ u_i^{n+1} = \frac{1}{2} \left(u_{i+1}^n + u_{i-1}^n\right) - \frac{\Delta t}{2\,\Delta x} \left( f( u_{i+1}^n ) - f( u_{i-1}^n ) \right). }[/math]

This method is conservative and first order accurate, hence quite dissipative. It can, however be used as a building block for building high-order numerical schemes for solving hyperbolic partial differential equations, much like Euler time steps can be used as a building block for creating high-order numerical integrators for ordinary differential equations.

We note that this method can be written in conservation form: [math]\displaystyle{ u_i^{n+1} = u^n_i - \frac{\Delta t}{ \Delta x} \left( \hat{f}^n_{i+1/2} - \hat{f}^n_{i-1/2} \right), }[/math] where [math]\displaystyle{ \hat{f}^n_{i-1/2} = \frac{1}{2} \left( f_{i-1} + f_{i} \right) - \frac{ \Delta x}{ 2 \Delta t } \left( u^n_{i} - u^n_{i-1} \right). }[/math]

Without the extra terms [math]\displaystyle{ u^n_i }[/math] and [math]\displaystyle{ u^n_{i-1} }[/math] in the discrete flux, [math]\displaystyle{ \hat{f}^n_{i-1/2} }[/math], one ends up with the FTCS scheme, which is well known to be unconditionally unstable for hyperbolic problems.

Stability and accuracy

Example problem initial condition

Lax-Friedrichs solution

This method is explicit and first order accurate in time and first order accurate in space ([math]\displaystyle{ O(\Delta t) + O({\Delta x^2}/{\Delta t})) }[/math] provided [math]\displaystyle{ u_0(x),\, u_b(t),\, u_c(t) }[/math] are sufficiently-smooth functions. Under these conditions, the method is stable if and only if the following condition is satisfied: [math]\displaystyle{ \left| a\frac{\Delta t}{\Delta x} \right| \leq 1. }[/math]

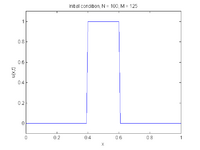
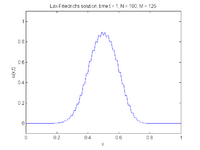
(A von Neumann stability analysis can show the necessity of this stability condition.) The Lax–Friedrichs method is classified as having second-order dissipation and third order dispersion.^[2] For functions that have discontinuities, the scheme displays strong dissipation and dispersion;^[3] see figures at right.

References

• DuChateau, Paul; Zachmann, David (2002), Applied Partial Differential Equations, New York: Dover Publications, ISBN 978-0-486-41976-3, https://archive.org/details/appliedpartialdi00duch 
• Press, William H; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 20.1.2. Lax Method", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8, http://apps.nrbook.com/empanel/index.html#pg=1034 

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Lax–Friedrichs method. Read more