Matrix completion

Matrix completion of a partially revealed 5 by 5 matrix with rank-1. Left: observed incomplete matrix; Right: matrix completion result.

Matrix completion is the task of filling in the missing entries of a partially observed matrix, which is equivalent to performing data imputation in statistics. A wide range of datasets are naturally organized in matrix form. One example is the movie-ratings matrix, as appears in the Netflix problem: Given a ratings matrix in which each entry [math]\displaystyle{ (i,j) }[/math] represents the rating of movie [math]\displaystyle{ j }[/math] by customer [math]\displaystyle{ i }[/math], if customer [math]\displaystyle{ i }[/math] has watched movie [math]\displaystyle{ j }[/math] and is otherwise missing, we would like to predict the remaining entries in order to make good recommendations to customers on what to watch next. Another example is the document-term matrix: The frequencies of words used in a collection of documents can be represented as a matrix, where each entry corresponds to the number of times the associated term appears in the indicated document.

Without any restrictions on the number of degrees of freedom in the completed matrix this problem is underdetermined since the hidden entries could be assigned arbitrary values. Thus we require some assumption on the matrix to create a well-posed problem, such as assuming it has maximal determinant, is positive definite, or is low-rank.^[1][2]

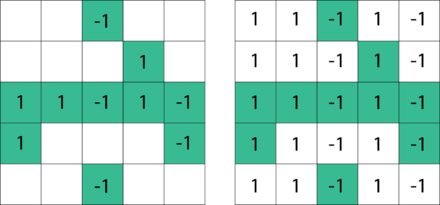
For example, one may assume the matrix has low-rank structure, and then seek to find the lowest rank matrix or, if the rank of the completed matrix is known, a matrix of rank [math]\displaystyle{ r }[/math] that matches the known entries. The illustration shows that a partially revealed rank-1 matrix (on the left) can be completed with zero-error (on the right) since all the rows with missing entries should be the same as the third row. In the case of the Netflix problem the ratings matrix is expected to be low-rank since user preferences can often be described by a few factors, such as the movie genre and time of release. Other applications include computer vision, where missing pixels in images need to be reconstructed, detecting the global positioning of sensors in a network from partial distance information, and multiclass learning. The matrix completion problem is in general NP-hard, but under additional assumptions there are efficient algorithms that achieve exact reconstruction with high probability.

In statistical learning point of view, the matrix completion problem is an application of matrix regularization which is a generalization of vector regularization. For example, in the low-rank matrix completion problem one may apply the regularization penalty taking the form of a nuclear norm [math]\displaystyle{ R(X) = \lambda\|X\|_* }[/math]

Low rank matrix completion

One of the variants of the matrix completion problem is to find the lowest rank matrix [math]\displaystyle{ X }[/math] which matches the matrix [math]\displaystyle{ M }[/math], which we wish to recover, for all entries in the set [math]\displaystyle{ E }[/math] of observed entries. The mathematical formulation of this problem is as follows:

[math]\displaystyle{ \begin{align} & \underset{X}{\text{min}} & \text{rank} (X) \\ & \text{subject to} & X_{ij} = M_{ij} & \;\; \forall i,j \in E\\ \end{align} }[/math]

Candès and Recht^[3] proved that with assumptions on the sampling of the observed entries and sufficiently many sampled entries this problem has a unique solution with high probability.

An equivalent formulation, given that the matrix [math]\displaystyle{ M }[/math] to be recovered is known to be of rank [math]\displaystyle{ r }[/math], is to solve for [math]\displaystyle{ X }[/math] where [math]\displaystyle{ X_{ij} = M_{ij} \;\; \forall i,j \in E }[/math]

Assumptions

A number of assumptions on the sampling of the observed entries and the number of sampled entries are frequently made to simplify the analysis and to ensure the problem is not underdetermined.

Uniform sampling of observed entries

To make the analysis tractable, it is often assumed that the set [math]\displaystyle{ E }[/math] of observed entries and fixed cardinality is sampled uniformly at random from the collection of all subsets of entries of cardinality [math]\displaystyle{ |E| }[/math]. To further simplify the analysis, it is instead assumed that [math]\displaystyle{ E }[/math] is constructed by Bernoulli sampling, i.e. that each entry is observed with probability [math]\displaystyle{ p }[/math]. If [math]\displaystyle{ p }[/math] is set to [math]\displaystyle{ \frac{N}{mn} }[/math] where [math]\displaystyle{ N }[/math] is the desired expected cardinality of [math]\displaystyle{ E }[/math], and [math]\displaystyle{ m,\;n }[/math] are the dimensions of the matrix (let [math]\displaystyle{ m \lt n }[/math] without loss of generality), [math]\displaystyle{ |E| }[/math] is within [math]\displaystyle{ O(n \log n) }[/math] of [math]\displaystyle{ N }[/math] with high probability, thus Bernoulli sampling is a good approximation for uniform sampling.^[3] Another simplification is to assume that entries are sampled independently and with replacement.^[4]

Lower bound on number of observed entries

Suppose the [math]\displaystyle{ m }[/math] by [math]\displaystyle{ n }[/math] matrix [math]\displaystyle{ M }[/math] (with [math]\displaystyle{ m \lt n }[/math]) we are trying to recover has rank [math]\displaystyle{ r }[/math]. There is an information theoretic lower bound on how many entries must be observed before [math]\displaystyle{ M }[/math] can be uniquely reconstructed. The set of [math]\displaystyle{ m }[/math] by [math]\displaystyle{ n }[/math] matrices with rank less than or equal to [math]\displaystyle{ r }[/math] is an algebraic variety in [math]\displaystyle{ {\mathbb C}^{m\times n} }[/math]with dimension [math]\displaystyle{ (n+m)r - r^2 }[/math]. Using this result, one can show that at least [math]\displaystyle{ 4nr - 4r^2 }[/math] entries must be observed for matrix completion in [math]\displaystyle{ {\mathbb C}^{n \times n} }[/math] to have a unique solution when [math]\displaystyle{ r \leq n/2 }[/math] .^[5]

Secondly, there must be at least one observed entry per row and column of [math]\displaystyle{ M }[/math]. The singular value decomposition of [math]\displaystyle{ M }[/math] is given by [math]\displaystyle{ U\Sigma V^\dagger }[/math]. If row [math]\displaystyle{ i }[/math] is unobserved, it is easy to see the [math]\displaystyle{ i^{\text{th}} }[/math] right singular vector of [math]\displaystyle{ M }[/math], [math]\displaystyle{ v_i }[/math], can be changed to some arbitrary value and still yield a matrix matching [math]\displaystyle{ M }[/math] over the set of observed entries. Similarly, if column [math]\displaystyle{ j }[/math] is unobserved, the [math]\displaystyle{ j^{\text{th}} }[/math] left singular vector of [math]\displaystyle{ M }[/math], [math]\displaystyle{ u_i }[/math] can be arbitrary. If we assume Bernoulli sampling of the set of observed entries, the Coupon collector effect implies that entries on the order of [math]\displaystyle{ O(n\log n) }[/math] must be observed to ensure that there is an observation from each row and column with high probability.^[6]

Combining the necessary conditions and assuming that [math]\displaystyle{ r \ll m, n }[/math] (a valid assumption for many practical applications), the lower bound on the number of observed entries required to prevent the problem of matrix completion from being underdetermined is on the order of [math]\displaystyle{ nr\log n }[/math].

Incoherence

The concept of incoherence arose in compressed sensing. It is introduced in the context of matrix completion to ensure the singular vectors of [math]\displaystyle{ M }[/math] are not too "sparse" in the sense that all coordinates of each singular vector are of comparable magnitude instead of just a few coordinates having significantly larger magnitudes.^[7][8] The standard basis vectors are then undesirable as singular vectors, and the vector [math]\displaystyle{ \frac{1}{\sqrt{n}} \begin{bmatrix} 1 \\ 1 \\ \vdots \\ 1 \end{bmatrix} }[/math] in [math]\displaystyle{ \mathbb{R}^n }[/math] is desirable. As an example of what could go wrong if the singular vectors are sufficiently "sparse", consider the [math]\displaystyle{ m }[/math] by [math]\displaystyle{ n }[/math] matrix [math]\displaystyle{ \begin{bmatrix} 1 & 0 & \cdots & 0 \\ \vdots & & \vdots \\ 0 & 0 & 0 & 0 \end{bmatrix} }[/math] with singular value decomposition [math]\displaystyle{ I_m \begin{bmatrix} 1 & 0 & \cdots & 0 \\ \vdots & & \vdots \\ 0 & 0 & 0 & 0 \end{bmatrix} I_n }[/math]. Almost all the entries of [math]\displaystyle{ M }[/math] must be sampled before it can be reconstructed.

Candès and Recht^[3] define the coherence of a matrix [math]\displaystyle{ U }[/math] with column space an [math]\displaystyle{ r- }[/math]dimensional subspace of [math]\displaystyle{ \mathbb{R}^n }[/math] as [math]\displaystyle{ \mu (U) = \frac{n}{r} \max_{i \lt n} \|P_U e_i\|^2 }[/math], where [math]\displaystyle{ P_U }[/math] is the orthogonal projection onto [math]\displaystyle{ U }[/math]. Incoherence then asserts that given the singular value decomposition [math]\displaystyle{ U\Sigma V^\dagger }[/math] of the [math]\displaystyle{ m }[/math] by [math]\displaystyle{ n }[/math] matrix [math]\displaystyle{ M }[/math],

1. [math]\displaystyle{ \mu (U), \; \mu (V) \leq \mu_0 }[/math]
2. The entries of [math]\displaystyle{ \sum_k u_k v_k ^\dagger }[/math] have magnitudes upper bounded by [math]\displaystyle{ \mu_1 \sqrt{\frac{r}{mn}} }[/math]

for some [math]\displaystyle{ \mu_0, \; \mu_1 }[/math].

Low rank matrix completion with noise

In real world application, one often observe only a few entries corrupted at least by a small amount of noise. For example, in the Netflix problem, the ratings are uncertain. Candès and Plan ^[9] showed that it is possible to fill in the many missing entries of large low-rank matrices from just a few noisy samples by nuclear norm minimization. The noisy model assumes that we observe

[math]\displaystyle{ Y_{ij} = M_{ij} + Z_{ij}, (i,j) \in \Omega, }[/math]

where [math]\displaystyle{ {Z_{ij}:(i,j) \in \Omega} }[/math] is a noise term. Note that the noise can be either stochastic or deterministic. Alternatively the model can be expressed as

[math]\displaystyle{ P_\Omega(Y) = P_\Omega(M) + P_\Omega(Z), }[/math]

where [math]\displaystyle{ Z }[/math] is an [math]\displaystyle{ n \times n }[/math] matrix with entries [math]\displaystyle{ Z_{ij} }[/math] for [math]\displaystyle{ (i,j) \in \Omega }[/math] assuming that [math]\displaystyle{ \|P_\Omega(Z)\|_F\leq\delta }[/math] for some [math]\displaystyle{ \delta \gt 0 }[/math] .To recover the incomplete matrix, we try to solve the following optimization problem:

[math]\displaystyle{ \begin{align} & \underset{X}{\text{min}} & \|X\|_* \\ & \text{subject to} & \|P_\Omega(X-Y)\|_F \leq \delta\\ \end{align} }[/math]

Among all matrices consistent with the data, find the one with minimum nuclear norm. Candès and Plan ^[9] have shown that this reconstruction is accurate. They have proved that when perfect noiseless recovery occurs, then matrix completion is stable vis a vis perturbations. The error is proportional to the noise level [math]\displaystyle{ \delta }[/math]. Therefore, when the noise level is small, the error is small. Here the matrix completion problem does not obey the restricted isometry property (RIP). For matrices, the RIP would assume that the sampling operator obeys

[math]\displaystyle{ (1-\delta)\|X\|^2_F \leq \frac{1}{p}\|P_\Omega(X)\|^2_F \leq (1+\delta)\|X\|^2_F }[/math]

for all matrices [math]\displaystyle{ X }[/math] with sufficiently small rank and [math]\displaystyle{ \delta\lt 1 }[/math] sufficiently small. The methods are also applicable to sparse signal recovery problems in which the RIP does not hold.

High rank matrix completion

The high rank matrix completion in general is NP-Hard. However, with certain assumptions, some incomplete high rank matrix or even full rank matrix can be completed.

Eriksson, Balzano and Nowak ^[10] have considered the problem of completing a matrix with the assumption that the columns of the matrix belong to a union of multiple low-rank subspaces. Since the columns belong to a union of subspaces, the problem may be viewed as a missing-data version of the subspace clustering problem. Let [math]\displaystyle{ X }[/math] be an [math]\displaystyle{ n \times N }[/math] matrix whose (complete) columns lie in a union of at most [math]\displaystyle{ k }[/math] subspaces, each of [math]\displaystyle{ rank \leq r \lt n }[/math], and assume [math]\displaystyle{ N \gg kn }[/math]. Eriksson, Balzano and Nowak ^[10] showed that under mild assumptions each column of [math]\displaystyle{ X }[/math] can be perfectly recovered with high probability from an incomplete version so long as at least [math]\displaystyle{ CrN\log^2(n) }[/math] entries of [math]\displaystyle{ X }[/math] are observed uniformly at random, with [math]\displaystyle{ C\gt 1 }[/math] a constant depending on the usual incoherence conditions, the geometrical arrangement of subspaces, and the distribution of columns over the subspaces.

The algorithm involves several steps: (1) local neighborhoods; (2) local subspaces; (3) subspace refinement; (4) full matrix completion. This method can be applied to Internet distance matrix completion and topology identification.

Algorithms for Low-Rank Matrix Completion

Various matrix completion algorithms have been proposed.^[8] These include convex relaxation-based algorithm,^[3] gradient-based algorithm,^[11] and alternating minimization-based algorithm.^[12]

Convex relaxation

The rank minimization problem is NP-hard. One approach, proposed by Candès and Recht, is to form a convex relaxation of the problem and minimize the nuclear norm [math]\displaystyle{ \|M\|_* }[/math] (which gives the sum of the singular values of [math]\displaystyle{ M }[/math]) instead of [math]\displaystyle{ \text{rank}(M) }[/math] (which counts the number of non zero singular values of [math]\displaystyle{ M }[/math]).^[3] This is analogous to minimizing the L1-norm rather than the L0-norm for vectors. The convex relaxation can be solved using semidefinite programming (SDP) by noticing that the optimization problem is equivalent to

[math]\displaystyle{ \begin{align} & \underset{W_1, W_2}{\text{min}} & & \text{trace} (W_1) + \text{trace} (W_2) \\ & \text{subject to} & & X_{ij} = M_{ij} \;\; \forall i,j \in E\\ & & & \begin{bmatrix} W_1 & X \\ X^T & W_2 \end{bmatrix} \succeq 0 \end{align} }[/math]

The complexity of using SDP to solve the convex relaxation is [math]\displaystyle{ O(\text{max}(m,n)^4) }[/math]. State of the art solvers like SDPT3 can only handle matrices of size up to 100 by 100 ^[13] An alternative first order method that approximately solves the convex relaxation is the Singular Value Thresholding Algorithm introduced by Cai, Candès and Shen.^[13]

Candès and Recht show, using the study of random variables on Banach spaces, that if the number of observed entries is on the order of [math]\displaystyle{ \max{\{\mu_1^2, \sqrt{\mu_0}\mu_1, \mu_0 n^{0.25}\}}nr \log n }[/math] (assume without loss of generality [math]\displaystyle{ m \lt n }[/math]), the rank minimization problem has a unique solution which also happens to be the solution of its convex relaxation with probability [math]\displaystyle{ 1-\frac{c}{n^3} }[/math] for some constant [math]\displaystyle{ c }[/math]. If the rank of [math]\displaystyle{ M }[/math] is small ([math]\displaystyle{ r \leq \frac{n^{0.2}}{\mu_0} }[/math]), the size of the set of observations reduces to the order of [math]\displaystyle{ \mu_0 n^{1.2} r \log n }[/math]. These results are near optimal, since the minimum number of entries that must be observed for the matrix completion problem to not be underdetermined is on the order of [math]\displaystyle{ nr \log n }[/math].

This result has been improved by Candès and Tao.^[6] They achieve bounds that differ from the optimal bounds only by polylogarithmic factors by strengthening the assumptions. Instead of the incoherence property, they assume the strong incoherence property with parameter [math]\displaystyle{ \mu_3 }[/math]. This property states that:

1. [math]\displaystyle{ | \langle e_a, P_U e_{a'} \rangle - \frac{r}{m} 1_{a = a'} | \leq \mu_3 \frac{\sqrt{r}}{m} }[/math] for [math]\displaystyle{ a, a' \leq m }[/math] and [math]\displaystyle{ | \langle e_b, P_U e_{b'} \rangle - \frac{r}{n} 1_{b = b'} | \leq \mu_3 \frac{\sqrt{r}}{n} }[/math] for [math]\displaystyle{ b, b' \leq n }[/math]
2. The entries of [math]\displaystyle{ \sum_i u_i v_i^\dagger }[/math] are bounded in magnitude by [math]\displaystyle{ \mu_3 \sqrt{\frac{r}{mn}} }[/math]

Intuitively, strong incoherence of a matrix [math]\displaystyle{ U }[/math] asserts that the orthogonal projections of standard basis vectors to [math]\displaystyle{ U }[/math] has magnitudes that have high likelihood if the singular vectors were distributed randomly.^[7]

Candès and Tao find that when [math]\displaystyle{ r }[/math] is [math]\displaystyle{ O(1) }[/math] and the number of observed entries is on the order of [math]\displaystyle{ \mu_3^4 n(\log n)^2 }[/math], the rank minimization problem has a unique solution which also happens to be the solution of its convex relaxation with probability [math]\displaystyle{ 1-\frac{c}{n^3} }[/math] for some constant [math]\displaystyle{ c }[/math]. For arbitrary [math]\displaystyle{ r }[/math], the number of observed entries sufficient for this assertion hold true is on the order of [math]\displaystyle{ \mu_3^2 nr (\log n)^6 }[/math]

Another convex relaxation approach ^[14] is to minimize the Frobenius squared norm under a rank constraint. This is equivalent to solving

[math]\displaystyle{ \begin{align} & \underset{X}{\text{min}} & & \Vert X \Vert_F^2 \\ & \text{subject to} & & X_{ij} = M_{ij} \;\; \forall i,j \in E\\ & & & \text{Rank}(X) \leq k. \end{align} }[/math]

By introducing an orthogonal projection matrix [math]\displaystyle{ Y }[/math] (meaning [math]\displaystyle{ Y^2=Y, Y=Y' }[/math]) to model the rank of [math]\displaystyle{ X }[/math] via [math]\displaystyle{ X=YX, \text{trace}(Y)\leq k }[/math] and taking this problem's convex relaxation, we obtain the following semidefinite program

[math]\displaystyle{ \begin{align} & \underset{X, Y, \theta}{\text{min}} & & \text{trace}(\theta) \\ & \text{subject to} & & X_{ij} = M_{ij} \;\; \forall i,j \in E\\ & & & \text{trace}(Y) \leq k, 0 \preceq Y \preceq I\\ & & & \begin{pmatrix} Y & X \\ X^\top & \theta \end{pmatrix}\succeq 0. \end{align} }[/math]

If Y is a projection matrix (i.e., has binary eigenvalues) in this relaxation, then the relaxation is tight. Otherwise, it gives a valid lower bound on the overall objective. Moreover, it can be converted into a feasible solution with a (slightly) larger objective by rounding the eigenvalues of Y greedily.^[14] Remarkably, this convex relaxation can be solved by alternating minimization on X and Y without solving any SDPs, and thus it scales beyond the typical numerical limits of state-of-the-art SDP solvers like SDPT3 or Mosek.

This approach is a special case of a more general reformulation technique, which can be applied to obtain a valid lower bound on any low-rank problem with a trace-matrix-convex objective.^[15]

Gradient descent

Keshavan, Montanari and Oh^[11] consider a variant of matrix completion where the rank of the [math]\displaystyle{ m }[/math] by [math]\displaystyle{ n }[/math] matrix [math]\displaystyle{ M }[/math], which is to be recovered, is known to be [math]\displaystyle{ r }[/math]. They assume Bernoulli sampling of entries, constant aspect ratio [math]\displaystyle{ \frac{m}{n} }[/math], bounded magnitude of entries of [math]\displaystyle{ M }[/math] (let the upper bound be [math]\displaystyle{ M_{\text{max}} }[/math]), and constant condition number [math]\displaystyle{ \frac{\sigma_1}{\sigma_r} }[/math] (where [math]\displaystyle{ \sigma_1 }[/math] and [math]\displaystyle{ \sigma_r }[/math] are the largest and smallest singular values of [math]\displaystyle{ M }[/math] respectively). Further, they assume the two incoherence conditions are satisfied with [math]\displaystyle{ \mu_0 }[/math] and [math]\displaystyle{ \mu_1 \frac{\sigma_1}{\sigma_r} }[/math] where [math]\displaystyle{ \mu_0 }[/math] and [math]\displaystyle{ \mu_1 }[/math] are constants. Let [math]\displaystyle{ M^E }[/math] be a matrix that matches [math]\displaystyle{ M }[/math] on the set [math]\displaystyle{ E }[/math] of observed entries and is 0 elsewhere. They then propose the following algorithm:

1. Trim [math]\displaystyle{ M^E }[/math] by removing all observations from columns with degree larger than [math]\displaystyle{ \frac{2|E|}{n} }[/math] by setting the entries in the columns to 0. Similarly remove all observations from rows with degree larger than [math]\displaystyle{ \frac{2|E|}{n} }[/math].
2. Project [math]\displaystyle{ M^E }[/math] onto its first [math]\displaystyle{ r }[/math] principal components. Call the resulting matrix [math]\displaystyle{ \text{Tr}(M^E) }[/math].
3. Solve [math]\displaystyle{ \min_{X,Y} \min_{S \in \mathbb{R}^{r \times r}} \frac{1}{2} \sum_{i,j \in E} (M_{ij} - (XSY^\dagger)_{ij})^2 + \rho G(X,Y) }[/math] where [math]\displaystyle{ G(X,Y) }[/math] is some regularization function by gradient descent with line search. Initialize [math]\displaystyle{ X,\;Y }[/math] at [math]\displaystyle{ X_0,\;Y_0 }[/math] where [math]\displaystyle{ \text{Tr}(M_E) = X_0 S_0 Y_0^\dagger }[/math]. Set [math]\displaystyle{ G(X,Y) }[/math] as some function forcing [math]\displaystyle{ X, \; Y }[/math] to remain incoherent throughout gradient descent if [math]\displaystyle{ X_0 }[/math] and [math]\displaystyle{ Y_0 }[/math] are incoherent.
4. Return the matrix [math]\displaystyle{ XSY^\dagger }[/math].

Steps 1 and 2 of the algorithm yield a matrix [math]\displaystyle{ \text{Tr}(M^E) }[/math] very close to the true matrix [math]\displaystyle{ M }[/math] (as measured by the root mean square error (RMSE)) with high probability. In particular, with probability [math]\displaystyle{ 1-\frac{1}{n^3} }[/math], [math]\displaystyle{ \frac{1}{mnM_{\text{max}}^2} \| M - \text{Tr}(M^E) \|_F^2 \leq C \frac{r}{m|E|} \sqrt{\frac{m}{n}} }[/math] for some constant [math]\displaystyle{ C }[/math]. [math]\displaystyle{ \| \cdot \|_F }[/math] denotes the Frobenius norm. Note that the full suite of assumptions is not needed for this result to hold. The incoherence condition, for example, only comes into play in exact reconstruction. Finally, although trimming may seem counter intuitive as it involves throwing out information, it ensures projecting [math]\displaystyle{ M^E }[/math] onto its first [math]\displaystyle{ r }[/math] principal components gives more information about the underlying matrix [math]\displaystyle{ M }[/math] than about the observed entries.

In Step 3, the space of candidate matrices [math]\displaystyle{ X,\;Y }[/math] can be reduced by noticing that the inner minimization problem has the same solution for [math]\displaystyle{ (X,Y) }[/math] as for [math]\displaystyle{ (XQ,YR) }[/math] where [math]\displaystyle{ Q }[/math] and [math]\displaystyle{ R }[/math] are orthonormal [math]\displaystyle{ r }[/math] by [math]\displaystyle{ r }[/math] matrices. Then gradient descent can be performed over the cross product of two Grassman manifolds. If [math]\displaystyle{ r \ll m,\;n }[/math] and the observed entry set is in the order of [math]\displaystyle{ nr\log n }[/math], the matrix returned by Step 3 is exactly [math]\displaystyle{ M }[/math]. Then the algorithm is order optimal, since we know that for the matrix completion problem to not be underdetermined the number of entries must be in the order of [math]\displaystyle{ nr\log n }[/math].

Alternating least squares minimization

Alternating minimization represents a widely applicable and empirically successful approach for finding low-rank matrices that best fit the given data. For example, for the problem of low-rank matrix completion, this method is believed to be one of the most accurate and efficient, and formed a major component of the winning entry in the Netflix problem. In the alternating minimization approach, the low-rank target matrix is written in a bilinear form:

[math]\displaystyle{ X= UV^T }[/math];

the algorithm then alternates between finding the best [math]\displaystyle{ U }[/math] and the best [math]\displaystyle{ V }[/math]. While the overall problem is non-convex, each sub-problem is typically convex and can be solved efficiently. Jain, Netrapalli and Sanghavi ^[12] have given one of the first guarantees for performance of alternating minimization for both matrix completion and matrix sensing.

The alternating minimization algorithm can be viewed as an approximate way to solve the following non-convex problem:

[math]\displaystyle{ \begin{align} & \underset{U, V \in \mathbb{R}^{n\times k}}{\text{min}} & \|P_\Omega(UV^T)-P_\Omega(M)\|^2_F \\ \end{align} }[/math]

The AltMinComplete Algorithm proposed by Jain, Netrapalli and Sanghavi is listed here:^[12]

1. Input: observed set [math]\displaystyle{ \Omega }[/math], values [math]\displaystyle{ P_\Omega(M) }[/math]
2. Partition [math]\displaystyle{ \Omega }[/math] into [math]\displaystyle{ 2T+1 }[/math] subsets [math]\displaystyle{ \Omega_0,\cdots,\Omega_{2T} }[/math] with each element of [math]\displaystyle{ \Omega }[/math] belonging to one of the [math]\displaystyle{ \Omega_t }[/math] with equal probability (sampling with replacement)
3. [math]\displaystyle{ \hat{U}^0 = SVD(\frac{1}{p}P_{\Omega_0}(M), k) }[/math] i.e., top-[math]\displaystyle{ k }[/math] left singular vectors of [math]\displaystyle{ \frac{1}{p}P_{\Omega_0}(M) }[/math]
4. Clipping: Set all elements of [math]\displaystyle{ \hat{U}^0 }[/math] that have magnitude greater than [math]\displaystyle{ \frac{2\mu\sqrt{k}}{\sqrt{n}} }[/math] to zero and orthonormalize the columns of [math]\displaystyle{ \hat{U}^0 }[/math]
5. for [math]\displaystyle{ t = 0, \cdots, T-1 }[/math] do
6. [math]\displaystyle{ \quad \hat{V}^{t+1}\leftarrow \text{argmin}_{V\in \mathbb{R}^{n\times k}}\|P_{\Omega_{t+1}}(\hat{U}V^T-M)\|^2_F }[/math]
7. [math]\displaystyle{ \quad \hat{U}^{t+1}\leftarrow \text{argmin}_{U\in \mathbb{R}^{m\times k}}\|P_{\Omega_{T+t+1}}(U(\hat{V}^{t+1})^T-M)\|^2_F }[/math]
8. end for
9. Return [math]\displaystyle{ X= \hat{U}^T(\hat{V}^T)^T }[/math]

They showed that by observing [math]\displaystyle{ |\Omega| = O((\frac{\sigma_1^*}{\sigma_k^*})^6k^7\log n \log (k \|M\|_F/\epsilon)) }[/math] random entries of an incoherent matrix [math]\displaystyle{ M }[/math], AltMinComplete algorithm can recover [math]\displaystyle{ M }[/math] in [math]\displaystyle{ O(\log(1/\epsilon)) }[/math] steps. In terms of sample complexity ([math]\displaystyle{ |\Omega| }[/math]), theoretically, Alternating Minimization may require a bigger [math]\displaystyle{ \Omega }[/math] than Convex Relaxation. However empirically it seems not the case which implies that the sample complexity bounds can be further tightened. In terms of time complexity, they showed that AltMinComplete needs time

[math]\displaystyle{ O(|\Omega|k^2\log(1/\epsilon)) }[/math].

It is worth noting that, although convex relaxation based methods have rigorous analysis, alternating minimization based algorithms are more successful in practice.^{[citation needed]}

Applications

Several applications of matrix completion are summarized by Candès and Plan^[9] as follows:

Collaborative filtering

Collaborative filtering is the task of making automatic predictions about the interests of a user by collecting taste information from many users. Companies like Apple, Amazon, Barnes and Noble, and Netflix are trying to predict their user preferences from partial knowledge. In these kind of matrix completion problem, the unknown full matrix is often considered low rank because only a few factors typically contribute to an individual's tastes or preference.

System identification

In control, one would like to fit a discrete-time linear time-invariant state-space model

[math]\displaystyle{ \begin{align} x(t+1)&=Ax(t)+Bu(t)\\ y(t)&=Cx(t)+Du(t) \end{align} }[/math]

to a sequence of inputs [math]\displaystyle{ u(t) \in \mathbb{R}^m }[/math] and outputs [math]\displaystyle{ y(t) \in \mathbb{R}^p, t = 0, \ldots, N }[/math]. The vector [math]\displaystyle{ x(t) \in \mathbb{R}^n }[/math] is the state of the system at time [math]\displaystyle{ t }[/math] and [math]\displaystyle{ n }[/math] is the order of the system model. From the input/output pair, one would like to recover the matrices [math]\displaystyle{ A,B,C,D }[/math] and the initial state [math]\displaystyle{ x(0) }[/math]. This problem can also be viewed as a low-rank matrix completion problem.

Internet of things (IoT) localization

The localization (or global positioning) problem emerges naturally in IoT sensor networks. The problem is to recover the sensor map in Euclidean space from a local or partial set of pairwise distances. Thus it is a matrix completion problem with rank two if the sensors are located in a 2-D plane and three if they are in a 3-D space.^[16]

Social Networks Recovery

Most of the real-world social networks have low-rank distance matrices. When we are not able to measure the complete network, which can be due to reasons such as private nodes, limited storage or compute resources, we only have a fraction of distance entries known. Criminal networks are a good example of such networks. Low-rank Matrix Completion can be used to recover these unobserved distances.^[17]

See also

• Matrix regularization
• Netflix Prize
• Collaborative filtering
• System identification
• Convex optimization
• Imputation

References

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Matrix completion. Read more