Matroid partitioning

Matroid partitioning is a problem arising in the mathematical study of matroids and in the design and analysis of algorithms. Its goal is to partition the elements of a matroid into as few independent sets as possible. An example is the problem of computing the arboricity of an undirected graph, the minimum number of forests needed to cover all of its edges. Matroid partitioning may be solved in polynomial time, given an independence oracle for the matroid. It may be generalized to show that a matroid sum is itself a matroid, to provide an algorithm for computing ranks and independent sets in matroid sums, and to compute the largest common independent set in the intersection of two given matroids.^[1]

Example

A partition of the edges of the complete bipartite graph K_4,4 into three forests, showing that it has arboricity at most three

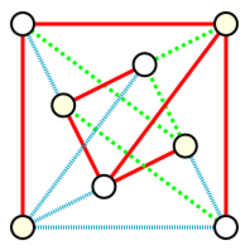
The arboricity of an undirected graph is the minimum number of forests into which its edges can be partitioned, or equivalently (by adding overlapping edges to each forest as necessary) the minimum number of spanning forests whose union is the whole graph. A formula proved by Crispin Nash-Williams characterizes the arboricity exactly: it is the maximum, over all subgraphs [math]\displaystyle{ H }[/math] of the given graph [math]\displaystyle{ G }[/math], of the quantity [math]\displaystyle{ \left\lceil\frac{|E(H)|}{|V(H)|-1}\right\rceil }[/math].^[2]

The forests of a graph form the independent sets of the associated graphic matroid, and the quantity [math]\displaystyle{ |V(H)|-1 }[/math] appearing in Nash-Williams' formula is the rank of the graphic matroid of [math]\displaystyle{ H }[/math], the maximum size of one of its independent sets. Thus, the problem of determining the arboricity of a graph is exactly the matroid partitioning problem for the graphic matroid. The fact that the [math]\displaystyle{ |E(H)| }[/math] elements of this matroid cannot be partitioned into fewer than [math]\displaystyle{ \frac{|E(H)|}{|V(H)|-1} }[/math] independent subsets is then just an application of the pigeonhole principle saying that, if [math]\displaystyle{ x }[/math] items are partitioned into sets of size at most [math]\displaystyle{ y }[/math], then at least [math]\displaystyle{ x/y }[/math] sets are needed. The harder direction of Nash-Williams' formula, which can be generalized to all matroids, is the proof that a partition of this size always exists.^[1]

Formula for partition size

To generalize Nash-Williams' formula, one may replace [math]\displaystyle{ G }[/math] by a matroid [math]\displaystyle{ M }[/math], and the subgraph [math]\displaystyle{ H }[/math] of [math]\displaystyle{ G }[/math] with a restriction [math]\displaystyle{ M|S }[/math] of [math]\displaystyle{ M }[/math] to a subset [math]\displaystyle{ S }[/math] of its elements. The number of edges of the subgraph [math]\displaystyle{ H }[/math] becomes, in this generalization, the cardinality [math]\displaystyle{ |S| }[/math] of the selected subset, and the formula [math]\displaystyle{ |V(H)|-1 }[/math] for the maximum size of a forest in [math]\displaystyle{ H }[/math] becomes the rank [math]\displaystyle{ r(S) }[/math]. Thus, the minimum number of independent sets in a partition of the given matroid [math]\displaystyle{ M }[/math] should be given by the formula

[math]\displaystyle{ k(M)=\max_S \left\lceil\frac{|S|}{r(S)}\right\rceil }[/math].

This formula is indeed valid, and it was given an algorithmic proof by (Edmonds 1965).^[1][3] In other words, a matroid can be partitioned into at most [math]\displaystyle{ k }[/math] independent subsets, if-and-only-if for every subset [math]\displaystyle{ S }[/math] of [math]\displaystyle{ M }[/math], the cardinality of [math]\displaystyle{ S }[/math] is at most [math]\displaystyle{ k\cdot r(S) }[/math].

Algorithms

The first algorithm for matroid partitioning was given by (Edmonds 1965).^[3] It is an incremental augmenting-path algorithm that considers the elements of the matroid one by one, in an arbitrary order, maintaining at each step of the algorithm an optimal partition for the elements that have been considered so far. At each step, when considering an element [math]\displaystyle{ x }[/math] that has not yet been placed into a partition, the algorithm constructs a directed graph that has as its nodes the elements that have already been partitioned, the new element [math]\displaystyle{ x }[/math], and a special element [math]\displaystyle{ \bot_i }[/math] for each of the [math]\displaystyle{ k }[/math] independent sets in the current partition. It then forms a directed graph [math]\displaystyle{ G_x }[/math] on this node set, with a directed arc [math]\displaystyle{ \bot_i\rightarrow y }[/math] for each matroid element [math]\displaystyle{ y }[/math] that can be added to partition set [math]\displaystyle{ i }[/math] without causing it to become dependent, and with a directed arc [math]\displaystyle{ z\rightarrow y }[/math] for each pair of matroid elements [math]\displaystyle{ (y,z) }[/math] such that removing [math]\displaystyle{ z }[/math] from its partition and replacing it with [math]\displaystyle{ y }[/math] forms another independent set.^[1][3]

Now there are two cases:

• If this graph contains a directed path from an element [math]\displaystyle{ \bot_i }[/math] to the newly considered element [math]\displaystyle{ x }[/math], then the shortest such path (or more generally any path that does not have any shortcutting edges) describes a sequence of changes that can be made simultaneously to the partition sets in order to form a new partition, with the same number of sets, that also includes [math]\displaystyle{ x }[/math]. In this case, the algorithm performs these changes and continues.
• If, on the other hand, no such path exists, then let [math]\displaystyle{ S }[/math] consist of the matroid elements from which [math]\displaystyle{ x }[/math] is reachable in [math]\displaystyle{ D }[/math]. Each set in the current partition must be a maximal independent set in the restriction [math]\displaystyle{ M|S }[/math], for if some element [math]\displaystyle{ y }[/math] of [math]\displaystyle{ S }[/math] could be added to partition set [math]\displaystyle{ i }[/math] in the restriction, then either there would exist an arc [math]\displaystyle{ \bot_i\rightarrow y }[/math] (if partition set [math]\displaystyle{ i }[/math] is non-maximal in the full matroid [math]\displaystyle{ M }[/math]) or an arc [math]\displaystyle{ z\rightarrow y }[/math] where [math]\displaystyle{ z\notin S }[/math] (if the partition set is non-maximal in [math]\displaystyle{ S }[/math] but maximal in the full matroid). In either case the existence of this arc contradicts the assumed construction of the set [math]\displaystyle{ S }[/math], and the contradiction proves that each partition set is maximal. Thus, by the easy direction of the matroid partitioning formula, the number of sets needed to partition [math]\displaystyle{ S }[/math] is at least

[math]\displaystyle{ \left\lceil\frac{|S|}{r(S)}\right\rceil=\left\lceil\frac{kr(S)+1}{r(S)}\right\rceil=k+1 }[/math],

so in this case the algorithm may find an optimal partition by placing [math]\displaystyle{ x }[/math] into its own new independent set and leaving the other independent sets unchanged.^[1][3]

The overall algorithm, then, considers each element [math]\displaystyle{ x }[/math] of the given matroid in turn, constructs the graph [math]\displaystyle{ G_x }[/math], tests which nodes can reach [math]\displaystyle{ x }[/math], and uses this information to update the current partition so that it includes [math]\displaystyle{ x }[/math]. At each step, the partition of the elements considered so far is optimal, so when the algorithm terminates it will have found an optimal partition for the whole matroid. Proving that this algorithm is correct requires showing that a shorcut-free path in the auxiliary graph always describes a sequence of operations that, when performed simultaneously, correctly preserves the independence of the sets in the partition; a proof of this fact was given by Edmonds. Because the algorithm only increases the number of sets in the partition when the matroid partitioning formula shows that a larger number is needed, the correctness of this algorithm also shows the correctness of the formula.^[1][3]

Although this algorithm depends only on the existence of an independence oracle for its correctness, faster algorithms can be found in many cases by taking advantage of the more specialized structure of specific types of matroids (such as graphic matroids) from which a particular partitioning problem has been defined.^[4]

Related problems

A matroid sum [math]\displaystyle{ \sum_i M_i }[/math] (where each [math]\displaystyle{ M_i }[/math] is a matroid) is itself a matroid, having as its elements the union of the elements of the summands. A set is independent in the sum if it can be partitioned into sets that are independent within each summand. The matroid partitioning algorithm generalizes to the problem of testing whether a set is independent in a matroid sum. Its correctness can be used to prove that a matroid sum is necessarily a matroid.^[3][4] An extended problem, that is also sometimes called matroid partition, is to find a largest set that is independent in the matroid sum, that is, a largest set that can be partitioned into sets that are disjoint in each input matroid. Cunningham^[5] presents an algorithm for solving this problem on O(n) n-element matroids using [math]\displaystyle{ O(n^{2.5}) }[/math] calls to an independence oracle.

The matroid intersection problem is finding the largest set that is independent in two matroids [math]\displaystyle{ M_1 }[/math] and [math]\displaystyle{ M_2 }[/math]. It may be solved by turning it into an equivalent matroid sum problem: if [math]\displaystyle{ B }[/math] is a basis of the sum [math]\displaystyle{ M_1+M_2^* }[/math], where [math]\displaystyle{ M_2^* }[/math] is the dual of [math]\displaystyle{ M_2 }[/math], then [math]\displaystyle{ B }[/math] must have full rank in [math]\displaystyle{ M_2^* }[/math] and removing a maximal independent set of [math]\displaystyle{ M_2^* }[/math] from [math]\displaystyle{ B }[/math] leaves a maximum intersection.^[6]

Matroid partitioning is a form of set cover problem, and the corresponding set packing problem (find a maximum number of disjoint spanning sets within a given matroid) is also of interest. It can be solved by algorithms similar to those for matroid partitioning.^[4] The fractional set packing and set covering problems associated with a matroid (that is, assign a weight to each independent set in such a way that for every element the total weight of the sets containing it is at most one or at least one, maximizing or minimizing the total weight of all the sets, respectively) can also be solved in polynomial time using matroid partitioning methods.^[1]

As well as its use in calculating the arboricity of a graph, matroid partitioning can be used with other matroids to find a subgraph of a given graph whose average degree is maximum, and to find the edge toughness of a graph (a variant of graph toughness involving the deletion of edges in place of vertices).^[1]

Matroid-constrained number partitioning is a different problem in which k (the number of subsets in the partition) is fixed. There are k different matroids over the same ground set, and the goal is to partition the ground set into k subsets, such that each subset i is an independent set in matroid i. Subject to this constraint, some objective function should be minimized. In a generalization of this variant, each of the k matroids has a weight, and the objective function depends on the weights (maximum weight, minimum weight or sum of weights).

References

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Matroid partitioning. Read more