Mnemonics in trigonometry

In trigonometry, it is common to use mnemonics to help remember trigonometric identities and the relationships between the various trigonometric functions.

SOH-CAH-TOA

Image mnemonic to help remember the ratios of sides of a right triangle

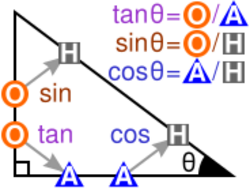
The sine, cosine, and tangent ratios in a right triangle can be remembered by representing them as strings of letters, for instance SOH-CAH-TOA in English:

Sine = Opposite ÷ Hypotenuse

Cosine = Adjacent ÷ Hypotenuse

Tangent = Opposite ÷ Adjacent

One way to remember the letters is to sound them out phonetically (i.e. /ˌsoʊkəˈtoʊə/ SOH-kə-TOH-ə, similar to Krakatoa).^[1]

Phrases

Another method is to expand the letters into a sentence, such as "Some Old Horses Chew Apples Happily Throughout Old Age", "Some Old Hippy Caught Another Hippy Tripping On Acid", or "Studying Our Homework Can Always Help To Obtain Achievement". The order may be switched, as in "Tommy On A Ship Of His Caught A Herring" (tangent, sine, cosine) or "The Old Army Colonel And His Son Often Hiccup" (tangent, cosine, sine) or "Come And Have Some Oranges Help To Overcome Amnesia" (cosine, sine, tangent).^[2][3] Communities in Chinese circles may choose to remember it as TOA-CAH-SOH, which also means 'big-footed woman' (Chinese: 大腳嫂; Pe̍h-ōe-jī: tōa-kha-só) in Hokkien.^{[citation needed]}

An alternate way to remember the letters for Sin, Cos, and Tan is to memorize the syllables Oh, Ah, Oh-Ah (i.e. /oʊ ə ˈoʊ.ə/) for O/H, A/H, O/A.^[4] Longer mnemonics for these letters include "Oscar Has A Hold On Angie" and "Oscar Had A Heap of Apples."^[2]

All Students Take Calculus

Signs of trigonometric functions in each quadrant.

All Students Take Calculus is a mnemonic for the sign of each trigonometric functions in each quadrant of the plane. The letters ASTC signify which of the trigonometric functions are positive, starting in the top right 1st quadrant and moving counterclockwise through quadrants 2 to 4.

• Quadrant I (angles from 0 to 90 degrees, or 0 to π/2 radians): All trigonometric functions are positive in this quadrant.
• Quadrant II (angles from 90 to 180 degrees, or π/2 to π radians): Sine and cosecant functions are positive in this quadrant.
• Quadrant III (angles from 180 to 270 degrees, or π to 3π/2 radians): Tangent and cotangent functions are positive in this quadrant.
• Quadrant IV (angles from 270 to 360 degrees, or 3π/2 to 2π radians): Cosine and secant functions are positive in this quadrant.

Other mnemonics include:

• All Stations To Central^[5]
• All Silly Tom Cats^[5]
• Add Sugar To Coffee^[5]
• All Science Teachers (are) Crazy^[6]
• A Smart Trig Class^[7]

Other easy-to-remember mnemonics are the ACTS and CAST laws. These have the disadvantages of not going sequentially from quadrants 1 to 4 and not reinforcing the numbering convention of the quadrants.

• CAST still goes counterclockwise but starts in quadrant 4 going through quadrants 4, 1, 2, then 3.
• ACTS still starts in quadrant 1 but goes clockwise going through quadrants 1, 4, 3, then 2.

Sines and cosines of special angles

Sines and cosines of common angles 0°, 30°, 45°, 60° and 90° follow the pattern [math]\displaystyle{ \frac{\sqrt{n}}{2} }[/math] with n = 0, 1, ..., 4 for sine and n = 4, 3, ..., 0 for cosine, respectively:^[8]

Hexagon chart

Trigonometric identities mnemonic

Another mnemonic permits all of the basic identities to be read off quickly. The hexagonal chart can be constructed with a little thought:^[9]

1. Draw three triangles pointing down, touching at a single point. This resembles a fallout shelter trefoil.
2. Write a 1 in the middle where the three triangles touch
3. Write the functions without "co" on the three left outer vertices (from top to bottom: sine, tangent, secant)
4. Write the co-functions on the corresponding three right outer vertices (cosine, cotangent, cosecant)

Starting at any vertex of the resulting hexagon:

• The starting vertex equals one over the opposite vertex. For example, [math]\displaystyle{ \sin A = \frac{{1}}{{\csc A}} }[/math]
• Going either clockwise or counter-clockwise, the starting vertex equals the next vertex divided by the vertex after that. For example, [math]\displaystyle{ \sin A = \frac{{\cos A}}{{\cot A}} = \frac{{\tan A}}{{\sec A}} }[/math]
• The starting corner equals the product of its two nearest neighbors. For example, [math]\displaystyle{ \sin A = \cos A \cdot \tan A }[/math]
• The sum of the squares of the two items at the top of a triangle equals the square of the item at the bottom. These are the trigonometric Pythagorean identities:

[math]\displaystyle{ \sin^2 A + \cos^2 A = 1 \ }[/math]

[math]\displaystyle{ 1 + \cot^2 A = \csc^2 A \ }[/math]

[math]\displaystyle{ \tan^2 A + 1 = \sec^2 A \ }[/math]

Aside from the last bullet, the specific values for each identity are summarized in this table:

See also

• List of trigonometric identities

References

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Mnemonics in trigonometry. Read more