Non-abelian group

Algebraic structure → Group theory Group theory
Basic notions Subgroup Normal subgroup Quotient group (Semi-)direct product Group homomorphisms kernel image direct sum wreath product simple finite infinite continuous multiplicative additive cyclic abelian dihedral nilpotent solvable List of group theory topics
Finite groups Classification of finite simple groups cyclic alternating Lie type sporadic Lagrange's theorem Sylow theorems Hall's theorem p-group Elementary abelian group Frobenius group Schur multiplier Symmetric group Sn Klein four-group V Dihedral group Dn Quaternion group Q Dicyclic group Dicn
Discrete groups Lattices Integers (Z) Free group Modular groups PSL(2,Z) SL(2,Z) Arithmetic group Lattice Hyperbolic group
Topological and Lie groups Solenoid Circle General linear GL(n) Special linear SL(n) Orthogonal O(n) Euclidean E(n) Special orthogonal SO(n) Unitary U(n) Special unitary SU(n) Symplectic Sp(n) G2 F4 E6 E7 E8 Lorentz Poincaré Conformal Diffeomorphism Loop Infinite dimensional Lie group O(∞) SU(∞) Sp(∞)
Algebraic groups Linear algebraic group Reductive group Abelian variety Elliptic curve
v t e

In mathematics, and specifically in group theory, a non-abelian group, sometimes called a non-commutative group, is a group (G, ∗) in which there exists at least one pair of elements a and b of G, such that a ∗ b ≠ b ∗ a.^[1][2] This class of groups contrasts with the abelian groups, where all pairs of group elements commute.

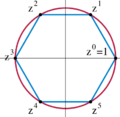
Non-abelian groups are pervasive in mathematics and physics. One of the simplest examples of a non-abelian group is the dihedral group of order 6. It is the smallest finite non-abelian group. A common example from physics is the rotation group SO(3) in three dimensions (for example, rotating something 90 degrees along one axis and then 90 degrees along a different axis is not the same as doing them in reverse order).

Both discrete groups and continuous groups may be non-abelian. Most of the interesting Lie groups are non-abelian, and these play an important role in gauge theory.

See also

• Associative algebra
• Noncommutative geometry
• Niels Henrik Abel

References

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Non-abelian group. Read more