Numerical differentiation

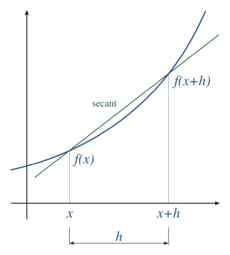
In numerical analysis, numerical differentiation algorithms estimate the derivative of a mathematical function or subroutine using values of the function and perhaps other knowledge about the function.

The simplest method is to use finite difference approximations.

A simple two-point estimation is to compute the slope of a nearby secant line through the points (x, f(x)) and (x + h, f(x + h)).^[1] Choosing a small number h, h represents a small change in x, and it can be either positive or negative. The slope of this line is $${\displaystyle \frac{f(x+h)-f(x)}{h}.}$$ This expression is Newton's difference quotient (also known as a first-order divided difference).

To obtain an error estimate for this approximation, one can use Taylor expansion of ${\displaystyle f(x)}$ about the base point ${\displaystyle x}$ to give $${\displaystyle f(x+h)=f(x)+h{f}^{\prime }(x)+\frac{h^2}{2}{f}^{″}(c)}$$ for some ${\displaystyle c}$ between ${\displaystyle x}$ and ${\displaystyle x+h}$. Rearranging gives $${\displaystyle f^{\prime }(x)=\underset{\text{Slope of secant line}}{\underbrace{\frac{f(x+h)-f(x)}{h}}}-\underset{\text{Error term}}{\underbrace{\frac{h}{2}{f}^{″}(c)}}.}$$ The slope of this secant line differs from the slope of the tangent line by an amount that is approximately proportional to h. As h approaches zero, the slope of the secant line approaches the slope of the tangent line and the error term vanishes. Therefore, the true derivative of f at x is the limit of the value of the difference quotient as the secant lines get closer and closer to being a tangent line: $${\displaystyle f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}.}$$

Since immediately substituting 0 for h results in ${\displaystyle \frac{0}{0}}$ indeterminate form, calculating the derivative directly can be unintuitive.

Equivalently, the slope could be estimated by employing positions x − h and x.

Another two-point formula is to compute the slope of a nearby secant line through the points (x − h, f(x − h)) and (x + h, f(x + h)). The slope of this line is $${\displaystyle \frac{f(x+h)-f(x-h)}{2h}.}$$

This formula is known as the symmetric difference quotient. In this case the first-order errors cancel, so the slope of these secant lines differ from the slope of the tangent line by an amount that is approximately proportional to ${\displaystyle h^2}$. Hence for small values of h this is a more accurate approximation to the tangent line than the one-sided estimation. However, although the slope is being computed at x, the value of the function at x is not involved.

The estimation error is given by $${\displaystyle R=\frac{-f^{(3)}(c)}{6}{h}^2,}$$ where ${\displaystyle c}$ is some point between ${\displaystyle x-h}$ and ${\displaystyle x+h}$. This error does not include the rounding error due to numbers being represented and calculations being performed in limited precision.

The symmetric difference quotient is employed as the method of approximating the derivative in a number of calculators, including TI-82, TI-83, TI-84, TI-85, all of which use this method with h = 0.001.^[2][3]

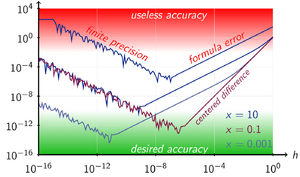
An important consideration in practice when the function is calculated using floating-point arithmetic of finite precision is the choice of step size, h. To illustrate, consider the two-point approximation formula with error term:

$${\displaystyle f^{\prime }(x)=\frac{f(x+h)-f(x-h)}{2h}-\frac{f^{(3)}(c)}{6}{h}^2}$$

where ${\displaystyle c}$ is some point between ${\displaystyle x-h}$ and ${\displaystyle x+h}$. Let ${\displaystyle e(x)}$ denote the roundoff error encountered when evaluating the function ${\displaystyle f(x)}$ and ${\displaystyle \hat{f}(x)}$ denote the computed value of ${\displaystyle f(x)}$. Therefore, $${\displaystyle f(x)=\hat{f}(x)+e(x).}$$ The total error in the approximation is $${\displaystyle f^{\prime }(x)-\frac{\hat{f}(x+h)-\hat{f}(x-h)}{2h}=\underset{\text{Roundoff error}}{\underbrace{\frac{e(x+h)-e(x-h)}{2h}}}-\underset{\text{Truncation error}}{\underbrace{\frac{f^{(3)}(c)}{6}{h}^2}}.}$$ Assuming that the roundoff errors are bounded by some number ${\displaystyle ϵ>0}$ and the third derivative of ${\displaystyle f(x)}$ is bounded by some number ${\displaystyle M>0}$, we get $${\displaystyle |f^{\prime }(x)-\frac{\hat{f}(x+h)-\hat{f}(x-h)}{2h}|\le \frac{ϵ}{h}+\frac{h^2}{6}M.}$$

To reduce the truncation error ${\displaystyle \frac{h^2}{6}M}$, we must reduce h. But as h is reduced, the roundoff error ${\displaystyle \frac{ϵ}{h}}$ increases. Due to the need to divide by the small value h, all the finite-difference formulae for numerical differentiation are similarly ill-conditioned^[4].

To demonstrate this difficulty, consider approximating the derivative of the function $${\displaystyle f(x)=\frac{2x}{1+\sqrt{x}}}$$ at the point ${\displaystyle x_0=9}$. In this case, we can calculate $${\displaystyle f^{\prime }(x)=\frac{2+\sqrt{x}}{(1+\sqrt{x}{)}^2}}$$ which gives $${\displaystyle f^{\prime }(9)=\frac{2+\sqrt{9}}{(1+\sqrt{9}{)}^2}=\frac{2+3}{(1+3{)}^2}=\frac{5}{16}=0.3125.}$$ Using 64-bit floating point numbers, the following approximations are generated with the two-point approximation formula and increasingly smaller step sizes. The smallest absolute error is produced for a step size of ${\displaystyle 10^{-4}}$, after which the absolute error steadily increases as the roundoff errors dominate calcuations.

For basic central differences, the optimal step is the cube-root of machine epsilon.^[5] For the numerical derivative formula evaluated at x and x + h, a choice for h that is small without producing a large rounding error is ${\displaystyle \sqrt{\epsilon }x}$ (though not when x = 0), where the machine epsilon ε is typically of the order of 2.2×10⁻¹⁶ for double precision.^[6] A formula for h that balances the rounding error against the secant error for optimum accuracy is^[7] $${\displaystyle h=2\sqrt{\epsilon \left|\frac{f(x)}{f^{″}(x)}\right|}}$$ (though not when ${\displaystyle f^{″}(x)=0}$), and to employ it will require knowledge of the function.

For computer calculations the problems are exacerbated because, although x necessarily holds a representable floating-point number in some precision (32 or 64-bit, etc.), x + h almost certainly will not be exactly representable in that precision. This means that x + h will be changed (by rounding or truncation) to a nearby machine-representable number, with the consequence that (x + h) − x will not equal h; the two function evaluations will not be exactly h apart. In this regard, since most decimal fractions are recurring sequences in binary (just as 1/3 is in decimal) a seemingly round step such as h = 0.1 will not be a round number in binary; it is 0.000110011001100...₂ A possible approach is as follows:

h     := sqrt(eps) * x;
xph   := x + h;
dx    := xph - x;
slope := (F(xph) - F(x)) / dx;

However, with computers, compiler optimization facilities may fail to attend to the details of actual computer arithmetic and instead apply the axioms of mathematics to deduce that dx and h are the same. With C and similar languages, a directive that xph is a volatile variable will prevent this.

To obtain more general derivative approximation formulas for some function ${\displaystyle f(x)}$, let ${\displaystyle h>0}$ be a positive number close to zero. The Taylor expansion of ${\displaystyle f(x)}$ about the base point ${\displaystyle x}$ is

${\displaystyle f(x+h)=f(x)+h{f}^{\prime }(x)+\frac{h^2}{2!}{f}^{″}(x)+\frac{h^3}{3!}{f}^{‴}(x)+...}$

(1)

Replacing ${\displaystyle h}$ by ${\displaystyle 2h}$ gives

${\displaystyle f(x+2h)=f(x)+2h{f}^{\prime }(x)+\frac{4h^2}{2!}{f}^{″}(x)+\frac{8h^3}{3!}{f}^{‴}(x)+...}$

(2)

Multiplying identity (1) by 4 gives

${\displaystyle 4f(x+h)=4f(x)+4h{f}^{\prime }(x)+\frac{4h^2}{2!}{f}^{″}(x)+\frac{4h^3}{3!}{f}^{‴}(x)+...}$

(1')

Subtracting identity (1') from (2) eliminates the ${\displaystyle h^2}$ term:

$${\displaystyle f(x+2h)-4f(x+h)=-3f(x)-2h{f}^{\prime }(x)+\frac{4h^3}{3!}{f}^{‴}(x)+...}$$

which can be written as

$${\displaystyle f(x+2h)-4f(x+h)=-3f(x)-2h{f}^{\prime }(x)+O(h^3).}$$

Rearranging terms gives $${\displaystyle f^{\prime }(x)=\frac{-3f(x)+4f(x+h)-f(x+2h)}{2h}+O(h^2),}$$

which is called the three-point forward difference formula for the derivative. Using a similar approach, one can show

$${\displaystyle f^{\prime }(x)=\frac{f(x+h)-f(x-h)}{2h}+O(h^2)}$$ which is called the three-point central difference formula, and $${\displaystyle f^{\prime }(x)=\frac{f(x-2h)-4f(x-h)+3f(x)}{2h}+O(h^2)}$$ which is called the three-point backward difference formula.

By a similar approach, the five point midpoint approximation formula can be derived as:^[8] $${\displaystyle f^{\prime }(x)=\frac{-f(x+2h)+8f(x+h)-8f(x-h)+f(x-2h)}{12h}+O(h^4).}$$

Consider approximating the derivative of ${\displaystyle f(x)=x\sin x}$ at the point ${\displaystyle x_0=\frac{\pi }{4}}$. Since ${\displaystyle f^{\prime }(x)=\sin x+x\cos x}$, the exact value is $${\displaystyle f^{\prime }(\frac{\pi }{4})=\sin \frac{\pi }{4}+\frac{\pi }{4}\cos \frac{\pi }{4}=\frac{1}{\sqrt{2}}+\frac{\pi }{4\sqrt{2}}\approx 1.2624671484563432.}$$

The following is an example of a Python implementation for finding derivatives numerically for ${\displaystyle f(x)=\frac{2x}{1+\sqrt{x}}}$ using the various three-point difference formulas at ${\displaystyle x_0=4}$. The function func has derivative func_prime.

import math

def func(x):
    return (2*x) / (1 + math.sqrt(x))

def func_prime(x):
    return (2 + math.sqrt(x)) / ((1 + math.sqrt(x))**2)

def three_point_forward(value, h):
    return ((-3/2) * func(value) + 2*func(value + h) - (1/2)*func(value + 2*h)) / h

def three_point_central(value, h):
    return ((-1/2)*func(value - h) + (1/2)*func(value + h)) / h

def three_point_backward(value, h):
    return ((1/2)*func(value - 2*h) - 2*func(value - h) + (3/2)*func(value)) / h

value = 4
actual = func_prime(value)

print("Actual value " + str(actual))
print("============================================")

for step_size in [0.1, 0.01, 0.001, 0.0001]:
    
    print("Step size " + str(step_size))

    forward = three_point_forward(value, step_size)
    backward = three_point_backward(value, step_size)
    central = three_point_central(value, step_size)
    
    print("Forward  {:>12}, Error = {:>12}".format(str(forward), str(abs(forward - actual))))
    print("Backward {:>12}, Error = {:>12}".format(str(forward), str(abs(backward - actual))))
    print("Central  {:>12}, Error = {:>12}".format(str(forward), str(abs(central - actual))))
    print("============================================")

Actual value 0.4444444444444444
============================================
Step size 0.1
Forward  0.4443963018050967, Error = 4.814263934771468e-05
Backward 0.4443963018050967, Error = 2.5082646145202503e-05
Central  0.4443963018050967, Error = 5.231976394060034e-05
============================================
Step size 0.01
Forward  0.4444439449793336, Error = 4.994651108258807e-07
Backward 0.4444439449793336, Error = 2.507721614808389e-07
Central  0.4444439449793336, Error = 5.036366184096863e-07
============================================
Step size 0.001
Forward  0.4444444394311464, Error = 5.013297998957e-09
Backward 0.4444444394311464, Error = 2.507574814458735e-09
Central  0.4444444394311464, Error = 5.017960935660426e-09
============================================
Step size 0.0001
Forward  0.4444444443896245, Error = 5.4819926376126205e-11
Backward 0.4444444443896245, Error = 2.5116131396885066e-11
Central  0.4444444443896245, Error = 5.037903427762558e-11
============================================

Using Taylor Series, it is possible to derive formulas to approximate the second (and higher order) derivatives of a general function. For a function ${\displaystyle f(x)}$ and some number ${\displaystyle h>0}$, expanding it about ${\displaystyle x+h}$ and ${\displaystyle x-h}$ gives

$${\displaystyle f(x+h)=f(x)+f^{\prime }(x)h+\frac{1}{2}{f}^{″}(x)h^2+\frac{1}{6}{f}^{‴}(x)h^3+\frac{1}{24}{f}^{(4)}({\xi }_1)h^4}$$ and $${\displaystyle f(x-h)=f(x)-f^{\prime }(x)h+\frac{1}{2}{f}^{″}(x)h^2-\frac{1}{6}{f}^{‴}(x)h^3+\frac{1}{24}{f}^{(4)}({\xi }_2)h^4}$$ where ${\displaystyle x-h<{\xi }_2<x<{\xi }_1<x+h}$. Adding these two equations gives

$${\displaystyle f(x+h)+f(x-h)=2f(x)+f^{″}(x)h^2+\frac{1}{24}[f^{(4)}({\xi }_1)+f^{(4)}({\xi }_2)]h^4.}$$

If ${\displaystyle f^{(4)}}$ is continuous on ${\displaystyle [x-h,x+h]}$, then ${\displaystyle \frac{1}{2}[f^{(4)}({\xi }_1)+f^{(4)}({\xi }_2)]}$ is between ${\displaystyle f^{(4)}({\xi }_1)}$ and ${\displaystyle f^{(4)}({\xi }_2)}$. The Intermediate Value Theorem guarantees a number, say ${\displaystyle \xi }$, between ${\displaystyle {\xi }_1}$ and ${\displaystyle {\xi }_2}$. We can therefore write

$${\displaystyle f^{″}(x)=\frac{1}{h^2}[f(x-h)-2f(x)+f(x+h)]-\frac{h^2}{12}{f}^{(4)}(\xi ).}$$

where ${\displaystyle x-h<\xi <x+h}$.

Consider approximating the second derivative of the function ${\displaystyle f(x)=e^x\sin x}$ at the point ${\displaystyle x_0=\frac{\pi }{4}}$.

Since ${\displaystyle f^{″}(x)=2e^x\cos x}$, the exact value is ${\displaystyle f^{″}(\frac{\pi }{4})=\sqrt{2}{e}^{\frac{\pi }{4}}\approx 3.1017663}$.

Using Newton's difference quotient, $${\displaystyle f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}}$$ the following can be shown^[9] (for n > 0): $${\displaystyle f^{(n)}(x)=\underset{h\to 0}{\lim }\frac{1}{h^n}{\displaystyle \sum _{k=0}^n}(-1{)}^{k+n}{\displaystyle (\genfrac{}{}{0ex}{}{n}{k})}f(x+kh)}$$

The classical finite-difference approximations for numerical differentiation are ill-conditioned. However, if ${\displaystyle f}$ is a holomorphic function, real-valued on the real line, which can be evaluated at points in the complex plane near ${\displaystyle x}$, then there are stable methods. For example,^[10] the first derivative can be calculated by the complex-step derivative formula:^[11][12][13] $${\displaystyle f^{\prime }(x)=\frac{\mathrm{\Im }(f(x+\mathrm{i}h))}{h}+O(h^2),{\mathrm{i}}^{\mathrm{2}}:=-1.}$$

The recommended step size to obtain accurate derivatives for a range of conditions is ${\displaystyle h=10^{-200}}$.^[14] This formula can be obtained by Taylor series expansion: $${\displaystyle f(x+\mathrm{i}h)=f(x)+\mathrm{i}h{f}^{\prime }(x)-\frac{1}{2!}{h}^2{f}^{″}(x)-\frac{\mathrm{i}}{3!}{h}^3{f}^{(3)}(x)+\cdots .}$$

The complex-step derivative formula is only valid for calculating first-order derivatives. A generalization of the above for calculating derivatives of any order employs multicomplex numbers, resulting in multicomplex derivatives.^[15][16][17] $${\displaystyle f^{(n)}(x)\approx \frac{{{𝒞}}_{n^2-1}^{(n)}(f(x+{\mathrm{i}}^{(1)}h+\cdots +{\mathrm{i}}^{(n)}h))}{h^n}}$$ where the ${\displaystyle {\mathrm{i}}^{(k)}}$ denote the multicomplex imaginary units; ${\displaystyle {\mathrm{i}}^{(1)}\equiv \mathrm{i}}$. The ${\displaystyle {{𝒞}}_k^{(n)}}$ operator extracts the ${\displaystyle k}$th component of a multicomplex number of level ${\displaystyle n}$, e.g., ${\displaystyle {{𝒞}}_0^{(n)}}$ extracts the real component and ${\displaystyle {{𝒞}}_{n^2-1}^{(n)}}$ extracts the last, “most imaginary” component. The method can be applied to mixed derivatives, e.g. for a second-order derivative $${\displaystyle \frac{{\partial }^{2}f(x,y)}{\partial x\partial y}\approx \frac{{{𝒞}}_3^{(2)}(f(x+{\mathrm{i}}^{(1)}h,y+{\mathrm{i}}^{(2)}h))}{h^2}}$$

A C++ implementation of multicomplex arithmetics is available.^[18]

In general, derivatives of any order can be calculated using Cauchy's integral formula:^[19] $${\displaystyle f^{(n)}(a)=\frac{n!}{2\pi i}{{\displaystyle \oint }}_{\gamma }\frac{f(z)}{(z-a{)}^{n+1}}\mathrm{d}z,}$$ where the integration is done numerically.

Using complex variables for numerical differentiation was started by Lyness and Moler in 1967.^[20] Their algorithm is applicable to higher-order derivatives.

A method based on numerical inversion of a complex Laplace transform was developed by Abate and Dubner.^[21] An algorithm that can be used without requiring knowledge about the method or the character of the function was developed by Fornberg.^[4]

Differential quadrature is the approximation of derivatives by using weighted sums of function values.^[22][23] Differential quadrature is of practical interest because its allows one to compute derivatives from noisy data. The name is in analogy with quadrature, meaning numerical integration, where weighted sums are used in methods such as Simpson's rule or the trapezoidal rule. There are various methods for determining the weight coefficients, for example, the Savitzky–Golay filter. Differential quadrature is used to solve partial differential equations. There are further methods for computing derivatives from noisy data.^[24]

• Automatic differentiation – Techniques to evaluate the derivative of a function specified by a computer program
• Five-point stencil
• List of numerical-analysis software
• Numerical integration – Methods of calculating definite integrals
• Numerical methods for ordinary differential equations – Methods used to find numerical solutions of ordinary differential equations
• Savitzky–Golay filter – Algorithm to smooth data points

Wikibooks has a book on the topic of: Numerical Methods

• Numerical Differentiation from wolfram.com
• NAG Library numerical differentiation routines
• Boost. Math numerical differentiation, including finite differencing and the complex step derivative
• Differentiation With(out) a Difference by Nicholas Higham, SIAM News.

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Numerical differentiation. Read more