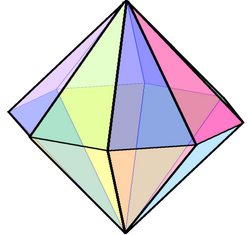
Octagonal bipyramid

Octagonal bipyramid
Type	bipyramid
Faces	16 triangles
Edges	24
Vertices	10
Schläfli symbol	{ } + {8}
Coxeter diagram
Symmetry group	D8h, [8,2], (*228), order 32
Rotation group	D8, [8,2]+, (228), order 16
Dual polyhedron	octagonal prism
Face configuration	V4.4.8
Properties	convex, face-transitive

The octagonal bipyramid is one of the infinite set of bipyramids, dual to the infinite prisms. If an octagonal bipyramid is to be face-transitive, all faces must be isosceles triangles. 16-sided dice are often octagonal bipyramids.

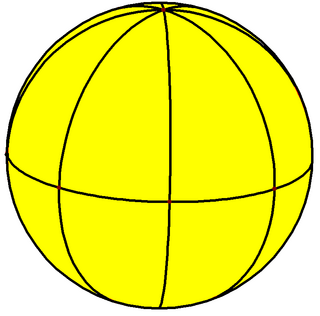
It can be drawn as a tiling on a sphere which also represents the fundamental domains of [4,2], *422 symmetry:

• Weisstein, Eric W.. "Dipyramid". http://mathworld.wolfram.com/Dipyramid.html. 
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra
  • VRML models <8>
  • Conway Notation for Polyhedra Try: dP8

0.00 (0 votes)