Orthoptic (geometry)

Short description: All points for which two tangents of a curve intersect at 90° angles

In the geometry of curves, an orthoptic is the set of points for which two tangents of a given curve meet at a right angle.

Parabola

Orthoptic of the parabola (its directrix)

Ellipse

Orthoptic of the ellipse (its director circle)

Minimum bounding box of the ellipse (circumscribed by the orthoptic circle)

Major and minor axes of the ellipse

Hyperbola

Orthoptic of the hyperbola (its director circle)

xy

-axes and hyperbolic asymptotes

Examples:

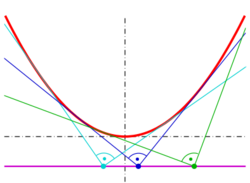
The orthoptic of a parabola is its directrix (proof: see below),
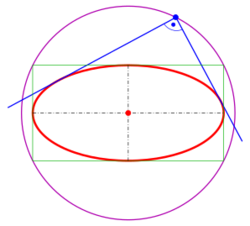
The orthoptic of an ellipse [math]\displaystyle{ \tfrac{x^2}{a^2} + \tfrac{y^2}{b^2} = 1 }[/math] is the director circle [math]\displaystyle{ x^2 + y^2 = a^2 + b^2 }[/math] (see below),
The orthoptic of a hyperbola [math]\displaystyle{ \tfrac{x^2}{a^2} - \tfrac{y^2}{b^2} = 1,\ a \gt b }[/math] is the director circle [math]\displaystyle{ x^2 + y^2 = a^2 - b^2 }[/math] (in case of $a \leq b$ there are no orthogonal tangents, see below),
The orthoptic of an astroid [math]\displaystyle{ x^{2/3} + y^{2/3} = 1 }[/math] is a quadrifolium with the polar equation [math]\displaystyle{ r=\tfrac{1}{\sqrt{2}}\cos(2\varphi), \ 0\le \varphi \lt 2\pi }[/math] (see below).

Generalizations:

An isoptic is the set of points for which two tangents of a given curve meet at a fixed angle (see below).
An isoptic of two plane curves is the set of points for which two tangents meet at a fixed angle.
Thales' theorem on a chord $PQ$ can be considered as the orthoptic of two circles which are degenerated to the two points $P$ and $Q$ .

Orthoptic of a parabola

Any parabola can be transformed by a rigid motion (angles are not changed) into a parabola with equation [math]\displaystyle{ y = ax^2 }[/math]. The slope at a point of the parabola is [math]\displaystyle{ m = 2ax }[/math]. Replacing $x$ gives the parametric representation of the parabola with the tangent slope as parameter: [math]\displaystyle{ \left(\tfrac{m}{2a},\tfrac{m^2}{4a} \right) \! . }[/math] The tangent has the equation [math]\displaystyle{ y=mx+n }[/math] with the still unknown $n$ , which can be determined by inserting the coordinates of the parabola point. One gets [math]\displaystyle{ y=mx-\tfrac{m^2}{4a}\; . }[/math]

If a tangent contains the point $(x 0, y 0)$ , off the parabola, then the equation [math]\displaystyle{ y_0 = m x_0 -\frac{m^2}{4a} \quad \rightarrow \quad m^2 - 4ax_0\,m + 4ay_0 = 0 }[/math] holds, which has two solutions $m 1$ and $m 2$ corresponding to the two tangents passing $(x 0, y 0)$ . The free term of a reduced quadratic equation is always the product of its solutions. Hence, if the tangents meet at $(x 0, y 0)$ orthogonally, the following equations hold: [math]\displaystyle{ m_1 m_2 = -1 = 4 a y_0 }[/math] The last equation is equivalent to [math]\displaystyle{ y_0 = -\frac{1}{4a}\, , }[/math] which is the equation of the directrix.

Orthoptic of an ellipse and hyperbola

Ellipse

Main page: Director circle

Let [math]\displaystyle{ E:\; \tfrac{x^2}{a^2} + \tfrac{y^2}{b^2} = 1 }[/math] be the ellipse of consideration.

The tangents to the ellipse [math]\displaystyle{ E }[/math] at the vertices and co-vertices intersect at the 4 points [math]\displaystyle{ (\pm a, \pm b) }[/math], which lie on the desired orthoptic curve (the circle [math]\displaystyle{ x^2+y^2 = a^2 + b^2 }[/math]).
The tangent at a point [math]\displaystyle{ (u,v) }[/math] of the ellipse [math]\displaystyle{ E }[/math] has the equation [math]\displaystyle{ \tfrac{u}{a^2} x + \tfrac{v}{b^2} y = 1 }[/math] (see tangent to an ellipse). If the point is not a vertex this equation can be solved for $y$ : [math]\displaystyle{ y = -\tfrac{b^2u}{a^2v}\;x\; + \;\tfrac{b^2}{v}\, . }[/math]

Using the abbreviations

[math]\displaystyle{ \begin{align} m &= -\tfrac{b^2u}{a^2v},\\ \color{red}n &= \color{red}\tfrac{b^2}{v} \end{align} }[/math]

(I)

and the equation [math]\displaystyle{ {\color{blue}\tfrac{u^2}{a^2} = 1 - \tfrac{v^2}{b^2} = 1-\tfrac{b^2}{n^2}} }[/math] one gets: [math]\displaystyle{ m^2 = \frac{b^4 u^2}{a^4 v^2} = \frac{1}{a^2} {\color{red}\frac{b^4}{v^2}} {\color{blue}\frac{u^2}{a^2}} = \frac{1}{a^2} {\color{red}n^2} {\color{blue}\left(1-\frac{b^2}{n^2}\right)} = \frac{n^2-b^2}{a^2}\, . }[/math] Hence

[math]\displaystyle{ n = \pm\sqrt{m^2 a^2 + b^2} }[/math]

(II)

and the equation of a non vertical tangent is [math]\displaystyle{ y = m x \pm \sqrt{m^2 a^2 + b^2}. }[/math] Solving relations (I) for [math]\displaystyle{ u,v }[/math] and respecting (II) leads to the slope depending parametric representation of the ellipse: [math]\displaystyle{ (u,v) = \left(-\tfrac{ma^2}{\pm\sqrt{m^2a^2+b^2}}\;,\;\tfrac{b^2}{\pm\sqrt{m^2a^2+b^2}}\right)\, . }[/math] (For another proof: see Ellipse § Parametric representation.)

If a tangent contains the point [math]\displaystyle{ (x_0,y_0) }[/math], off the ellipse, then the equation [math]\displaystyle{ y_0 = m x_0 \pm \sqrt{m^2a^2+b^2} }[/math] holds. Eliminating the square root leads to [math]\displaystyle{ m^2 - \frac{2x_0y_0}{x_0^2-a^2}m + \frac{y_0^2-b^2}{x_0^2-a^2} = 0, }[/math] which has two solutions [math]\displaystyle{ m_1,m_2 }[/math] corresponding to the two tangents passing through [math]\displaystyle{ (x_0,y_0) }[/math]. The constant term of a monic quadratic equation is always the product of its solutions. Hence, if the tangents meet at [math]\displaystyle{ (x_0,y_0) }[/math] orthogonally, the following equations hold:

Orthoptics (red circles) of a circle, ellipses and hyperbolas

[math]\displaystyle{ m_1 m_2 = -1 = \frac{y_0^2 - b^2}{x_0^2 - a^2} }[/math] The last equation is equivalent to [math]\displaystyle{ x_0^2+y_0^2 = a^2+b^2\, . }[/math] From (1) and (2) one gets:

The intersection points of orthogonal tangents are points of the circle [math]\displaystyle{ x^2 + y^2 = a^2 + b^2 }[/math].

Hyperbola

The ellipse case can be adopted nearly exactly to the hyperbola case. The only changes to be made are to replace [math]\displaystyle{ b^2 }[/math] with [math]\displaystyle{ -b^2 }[/math] and to restrict $m$ to $| m | > b / a$ . Therefore:

The intersection points of orthogonal tangents are points of the circle [math]\displaystyle{ x^2 + y^2 = a^2 - b^2 }[/math], where

a > b

.

Orthoptic of an astroid

Orthoptic (purple) of an astroid

An astroid can be described by the parametric representation [math]\displaystyle{ \mathbf c(t) = \left(\cos^3t, \sin^3t\right), \quad 0 \le t \lt 2\pi. }[/math] From the condition [math]\displaystyle{ \mathbf \dot c(t) \cdot \mathbf \dot c(t+\alpha) = 0 }[/math] one recognizes the distance $α$ in parameter space at which an orthogonal tangent to $ċ (t)$ appears. It turns out that the distance is independent of parameter $t$ , namely $α = \pm π / 2$ . The equations of the (orthogonal) tangents at the points $c (t)$ and $c (t + π / 2)$ are respectively: [math]\displaystyle{ \begin{align} y &= -\tan t \left(x-\cos^3 t\right) + \sin^3 t, \\ y &= \frac{1}{\tan t} \left(x+\sin^3 t\right) + \cos^3 t. \end{align} }[/math] Their common point has coordinates: [math]\displaystyle{ \begin{align} x &= \sin t \cos t \left(\sin t - \cos t\right), \\ y &= \sin t \cos t \left(\sin t + \cos t\right). \end{align} }[/math] This is simultaneously a parametric representation of the orthoptic.

Elimination of the parameter $t$ yields the implicit representation [math]\displaystyle{ 2\left(x^2+y^2\right)^3 - \left(x^2-y^2\right)^2 = 0. }[/math] Introducing the new parameter $φ = t - 5π / 4$ one gets [math]\displaystyle{ \begin{align} x &= \tfrac{1}{\sqrt{2}} \cos(2\varphi)\cos\varphi, \\ y &= \tfrac{1}{\sqrt{2}} \cos(2\varphi)\sin\varphi. \end{align} }[/math] (The proof uses the angle sum and difference identities.) Hence we get the polar representation [math]\displaystyle{ r = \tfrac{1}{\sqrt{2}} \cos(2\varphi), \quad 0 \le \varphi \lt 2\pi }[/math] of the orthoptic. Hence:

The orthoptic of an astroid is a quadrifolium.

Isoptic of a parabola, an ellipse and a hyperbola

Isoptics (purple) of a parabola for angles 80° and 100°

Isoptics (purple) of an ellipse for angles 80° and 100°

Isoptics (purple) of a hyperbola for angles 80° and 100°

Below the isotopics for angles $α \neq 90°$ are listed. They are called $α$ -isoptics. For the proofs see below.

Equations of the isoptics

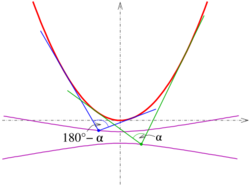
Parabola:

The $α$ -isoptics of the parabola with equation $y = ax 2$ are the branches of the hyperbola [math]\displaystyle{ x^2-\tan^2\alpha\left(y+\frac{1}{4a}\right)^2-\frac{y}{a}=0. }[/math] The branches of the hyperbola provide the isoptics for the two angles $α$ and $180° - α$ (see picture).

Ellipse:

The $α$ -isoptics of the ellipse with equation $x 2 / a 2 + y 2 / b 2 = 1$ are the two parts of the degree-4 curve [math]\displaystyle{ \left(x^2+y^2-a^2-b^2\right)^2 \tan^2\alpha = 4\left(a^2y^2 + b^2x^2 - a^2b^2\right) }[/math] (see picture).

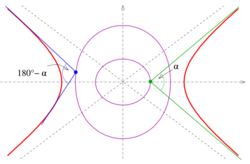
Hyperbola:

The $α$ -isoptics of the hyperbola with the equation $x 2 / a 2 - y 2 / b 2 = 1$ are the two parts of the degree-4 curve [math]\displaystyle{ \left(x^2 + y^2 - a^2 + b^2\right)^2 \tan^2\alpha = 4 \left(a^2y^2 - b^2x^2 + a^2b^2\right). }[/math]

Proofs

Parabola:

A parabola $y = ax 2$ can be parametrized by the slope of its tangents $m = 2 ax$ : [math]\displaystyle{ \mathbf c(m) = \left(\frac{m}{2a},\frac{m^2}{4a}\right), \quad m \in \R. }[/math]

The tangent with slope $m$ has the equation [math]\displaystyle{ y=mx-\frac{m^2}{4a}. }[/math]

The point $(x 0, y 0)$ is on the tangent if and only if [math]\displaystyle{ y_0 = m x_0 - \frac{m^2}{4a}. }[/math]

This means the slopes $m 1$ , $m 2$ of the two tangents containing $(x 0, y 0)$ fulfil the quadratic equation [math]\displaystyle{ m^2 - 4ax_0m + 4ay_0 = 0. }[/math]

If the tangents meet at angle $α$ or $180° - α$ , the equation [math]\displaystyle{ \tan^2\alpha = \left(\frac{m_1-m_2}{1+m_1 m_2}\right)^2 }[/math]

must be fulfilled. Solving the quadratic equation for $m$ , and inserting $m 1$ , $m 2$ into the last equation, one gets [math]\displaystyle{ x_0^2-\tan^2\alpha\left(y_0+\frac{1}{4a}\right)^2-\frac{y_0}{a} = 0. }[/math]

This is the equation of the hyperbola above. Its branches bear the two isoptics of the parabola for the two angles $α$ and $180° - α$ .

Ellipse:

In the case of an ellipse $x 2 / a 2 + y 2 / b 2 = 1$ one can adopt the idea for the orthoptic for the quadratic equation [math]\displaystyle{ m^2-\frac{2x_0y_0}{x_0^2-a^2}m + \frac{y_0^2-b^2}{x_0^2-a^2} = 0. }[/math]

Now, as in the case of a parabola, the quadratic equation has to be solved and the two solutions $m 1$ , $m 2$ must be inserted into the equation [math]\displaystyle{ \tan^2\alpha=\left(\frac{m_1-m_2}{1+m_1m_2}\right)^2. }[/math]

Rearranging shows that the isoptics are parts of the degree-4 curve: [math]\displaystyle{ \left(x_0^2+y_0^2-a^2-b^2\right)^2 \tan^2\alpha = 4\left(a^2y_0^2+b^2x_0^2-a^2b^2\right). }[/math]

Hyperbola:

The solution for the case of a hyperbola can be adopted from the ellipse case by replacing $b 2$ with $- b 2$ (as in the case of the orthoptics, see above).

To visualize the isoptics, see implicit curve.

External links

Notes

References

Lawrence, J. Dennis (1972). A catalog of special plane curves. Dover Publications. pp. 58–59. ISBN 0-486-60288-5. https://archive.org/details/catalogofspecial00lawr/page/58.
Odehnal, Boris (2010). "Equioptic Curves of Conic Sections". Journal for Geometry and Graphics 14 (1): 29–43. http://www.heldermann-verlag.de/jgg/jgg14/j14h1odeh.pdf.
Schaal, Hermann (1977). Lineare Algebra und Analytische Geometrie. III. Vieweg. p. 220. ISBN 3-528-03058-5.
Steiner, Jacob (1867). Vorlesungen über synthetische Geometrie. Leipzig: B. G. Teubner. Part 2, p. 186. https://archive.org/details/bub_gb_jCgPAAAAQAAJ.
Ternullo, Maurizio (2009). "Two new sets of ellipse related concyclic points". Journal of Geometry 94 (1–2): 159–173. doi:10.1007/s00022-009-0005-7.

0.00

(0 votes)

Original source: https://en.wikipedia.org/wiki/Orthoptic (geometry). Read more

v t e Differential transforms of plane curves
Unary operations	Evolute Involute Dual curve Inverse curve Parallel curve Isoptic
Unary operations defined by a point	Pedal & Contrapedal curves Negative pedal curve Pursuit curve Caustic
Unary operations defined by two points	Strophoid
Binary operations defined by a point	Roulette Cissoid
Operations on a family of curves	Envelope