Oval (projective plane)

Short description: Circle-like pointset in a geometric plane

To the definition of an oval:
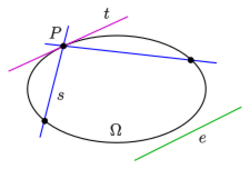
e: exterior (passing) line,
t: tangent,
s: secant

In projective geometry an oval is a point set in a plane that is defined by incidence properties. The standard examples are the nondegenerate conics. However, a conic is only defined in a pappian plane, whereas an oval may exist in any type of projective plane. In the literature, there are many criteria which imply that an oval is a conic, but there are many examples, both infinite and finite, of ovals in pappian planes which are not conics.

As mentioned, in projective geometry an oval is defined by incidence properties, but in other areas, ovals may be defined to satisfy other criteria, for instance, in differential geometry by differentiability conditions in the real plane.

The higher dimensional analog of an oval is an ovoid in a projective space.

A generalization of the oval concept is an abstract oval, which is a structure that is not necessarily embedded in a projective plane. Indeed, there exist abstract ovals which can not lie in any projective plane.

Definition of an oval

In a projective plane a set $Ω$ of points is called an oval, if:

Any line $l$ meets $Ω$ in at most two points, and
For any point $P \in Ω$ there exists exactly one tangent line $t$ through $P$ , i.e., $t \cap Ω = {P$ }.

For finite planes (i.e. the set of points is finite) we have a more convenient characterization:^[2]

For a finite projective plane of order $n$ (i.e. any line contains $n + 1$ points) a set $Ω$ of points is an oval if and only if $| Ω | = n + 1$ and no three points are collinear (on a common line).

A set of points in an affine plane satisfying the above definition is called an affine oval.

An affine oval is always a projective oval in the projective closure (adding a line at infinity) of the underlying affine plane.

An oval can also be considered as a special quadratic set.^[3]

Examples

Conic sections

projective conic in inhomogeneous coordinates: parabola plus point at infinity of the axis

projective conic in inhomogeneous coordinates: hyperbola plus points at infinity of the asymptotes

In any pappian projective plane there exist nondegenerate projective conic sections and any nondegenerate projective conic section is an oval. This statement can be verified by a straightforward calculation for any of the conics (such as the parabola or hyperbola).

Non-degenerate conics are ovals with special properties:

Pascal's Theorem and its various degenerations are valid.
There are many projectivities which leave a conic invariant.

Ovals, which are not conics

in the real plane

If one glues one half of a circle and a half of an ellipse smoothly together, one gets a non-conic oval.
If one takes the inhomogeneous representation of a conic oval as a parabola plus a point at infinity and replaces the expression $x 2$ by $x 4$ , one gets an oval which is not a conic.
If one takes the inhomogeneous representation of a conic oval as a hyperbola plus two points at infinity and replaces the expression $1 / x$ by $1 / x 3$ , one gets an oval which is not a conic.
The implicit curve $x 4 + y 4 = 1$ is a non conic oval.

in a finite plane of even order

In a finite pappian plane of even order a nondegenerate conic has a nucleus (a single point through which every tangent passes), which can be exchanged with any point of the conic to obtain an oval which is not a conic.
For the field $K = GF(2 m)$ with $2 m$ elements let

[math]\displaystyle{ \Omega=\{(x,y)\in K^2 \; | y=x^{2^k}\; \} \; \cup \; \{(\infty)\} }[/math]

For

k \in {2,..., m - 1}

and

k

and

m

coprime, the set

Ω

is an oval, which is not a conic.^[4]^[5]

Further finite examples can be found here:^[6]

Criteria for an oval to be a conic

For an oval to be a conic the oval and/or the plane has to fulfill additional conditions. Here are some results:

An oval in an arbitrary projective plane, which fulfills the incidence condition of Pascal's theorem or the 5-point degeneration of it, is a nondegenerate conic.^[7]
If $Ω$ is an oval in a pappian projective plane and the group of projectivities which leave $Ω$ invariant is 3-transitive, i.e. for 2 triples $A 1, A 2, A 3; B 1, B 2, B 3$ of points there exists a projectivity $π$ with $π(A i) = B i, i = 1,2,3$ . In the finite case 2-transitive is sufficient.^[8]
An oval $Ω$ in a pappian projective plane of characteristic $\neq 2$ is a conic if and only if for any point $P$ of a tangent there is an involutory perspectivity (symmetry) with center $P$ which leaves $Ω$ invariant.^[9]
If $Ω$ is an oval in a finite Desarguesian^[10] (pappian) projective plane of odd order, $PG(2, q)$ , then $Ω$ is a conic (Segre's theorem, (Segre 1955)). This implies that, after a possible change of coordinates, every oval of $PG(2, q)$ with $q$ odd has the parametrization :

[math]\displaystyle{ \{(t,t^2,1)\mid t\in GF(q)\}\cup \{(0,1,0)\}. }[/math]

For topological ovals the following simple criteria holds:

5. Any closed oval of the complex projective plane is a conic.^[11]

Further results on ovals in finite planes

An oval in a finite projective plane of order $q$ is a ( $q + 1, 2$ )-arc, in other words, a set of $q + 1$ points, no three collinear. Ovals in the Desarguesian (pappian) projective plane $PG(2, q)$ for $q$ odd are just the nonsingular conics. However, ovals in $PG(2, q)$ for $q$ even have not yet been classified.

In an arbitrary finite projective plane of odd order $q$ , no sets with more points than $q + 1$ , no three of which are collinear, exist, as first pointed out by Bose in a 1947 paper on applications of this sort of mathematics to the statistical design of experiments. Furthermore, by Qvist's theorem, through any point not on an oval there pass either zero or two tangent lines of that oval.

A hyperoval (the 4 red points) in the 7 point Fano plane.

When q is even, the situation is completely different.

In this case, sets of $q + 2$ points, no three of which collinear, may exist in a finite projective plane of order $q$ and they are called hyperovals; these are maximal arcs of degree 2.

Given an oval there is a unique tangent through each point, and if $q$ is even Qvist's theorem, ((Qvist 1952)) shows that all these tangents are concurrent in a point $P$ outside the oval. Adding this point (called the nucleus of the oval or sometimes the knot) to the oval gives a hyperoval. Conversely, removing any one point from a hyperoval immediately gives an oval.

As all ovals in the even order case are contained in hyperovals, a description of the (known) hyperovals implicitly gives all (known) ovals. The ovals obtained by removing a point from a hyperoval are projectively equivalent if and only if the removed points are in the same orbit of the automorphism group of the hyperoval. There are only three small examples (in the Desarguesian planes) where the automorphism group of the hyperoval is transitive on its points (see (Korchmáros 1978)) so, in general, there are different types of ovals contained in a single hyperoval.

Desarguesian Case: PG(2,2^h)

This is the most studied case and so the most is known about these hyperovals.

Every nonsingular conic in the projective plane, together with its nucleus, forms a hyperoval. These may be called hyperconics, but the more traditional term is regular hyperovals. For each of these sets, there is a system of coordinates such that the set is:

[math]\displaystyle{ \{(t,t^2,1)\mid t\in GF(q)\}\cup \{(0,1,0)\}\cup\{(1,0,0)\}. }[/math]

However, many other types of hyperovals of PG(2, q) can be found if q > 8. Hyperovals of PG(2, q) for q even have only been classified for q < 64 to date.

In PG(2,2^h), h > 0, a hyperoval contains at least four points no three of which are collinear. Thus, by the Fundamental Theorem of Projective Geometry we can always assume that the points with projective coordinates (1,0,0), (0,1,0), (0,0,1) and (1,1,1) are contained in any hyperoval. The remaining points of the hyperoval (when h > 1) will have the form (t, f(t),1) where t ranges through the values of the finite field GF(2^h) and f is a function on that field which represents a permutation and can be uniquely expressed as a polynomial of degree at most 2^h - 2, i.e. it is a permutation polynomial. Notice that f(0) = 0 and f(1) = 1 are forced by the assumption concerning the inclusion of the specified points. Other restrictions on f are forced by the no three points collinear condition. An f which produces a hyperoval in this way is called an o-polynomial. The following table lists all the known hyperovals (as of 2011) of PG(2,2^h) by giving the o-polynomial and any restrictions on the value of h that are necessary for the displayed function to be an o-polynomial. Note that all exponents are to be taken mod(2^h - 1).

Known Hyperovals in PG(2,2^h)

Name	O-Polynomial	Field Restriction	Reference
Hyperconic	f(t) = t²	None	Classical
Translation	[math]\displaystyle{ f(t) = t^{2^i} }[/math] (i,h) = 1	None	(Segre 1962)
Segre	f(t) = t⁶	h odd	(Segre 1962); (Segre Bartocci)
Glynn I	f(t) = t^3σ+4 (see below)	h odd	(Glynn 1983)
Glynn II	f(t) = t^σ+γ (see below)	h odd	(Glynn 1983)
Payne	f(t) = t^1/6+t^1/2+t^5/6	h odd	(Payne 1985)
Cherowitzo	f(t) = t^σ + t^σ+2 + t^3σ+4	h odd	(Cherowitzo 1986); (Cherowitzo 1998)
Subiaco	see a) below	None	(Cherowitzo Penttila)
Adelaide	see b) below	h even	(Cherowitzo O'Keefe)
Penttila-O'Keefe	see c) below	h = 5	(O'Keefe Penttila)
where [math]\displaystyle{ \gamma^4 \equiv \sigma^2 \equiv 2 (\bmod(2^h - 1)) }[/math].

^a) The Subiaco o-polynomial is given by: [math]\displaystyle{ f(t) = {{d^2 t^4 + d^2(1 + d + d^2) t^3 + d^2(1 + d + d^2)t^2 + d^2 t} \over {t^4 + d^2 t^2 + 1}} + t^{1/2}, }[/math] whenever [math]\displaystyle{ tr(1/d) = 1 \hbox { and }d \not\in GF(4) \hbox{ if } h \equiv 2 (\bmod 4) }[/math], where tr is the absolute trace function of GF(2^h). This o-polynomial gives rise to a unique hyperoval if [math]\displaystyle{ h \not\equiv 2 (\bmod 4) }[/math] and to two inequivalent hyperovals if [math]\displaystyle{ h \equiv 2 (\bmod 4), h \gt 2 }[/math].

^b) To describe the Adelaide hyperovals, we will start in a slightly more general setting. Let F = GF(q) and K = GF(q²). Let [math]\displaystyle{ b \in K }[/math] be an element of norm 1, different from 1, i.e. b^q+1 = 1, [math]\displaystyle{ b \neq 1 }[/math]. Consider the polynomial, for [math]\displaystyle{ t \in F }[/math],

f(t) = (tr(b))⁻¹tr(b^m)(t + 1) + (tr(b))⁻¹tr((bt + b^q)^m)(t + tr(b)t^½+ 1)^1−m + t^½,

where tr(x) = tr_K/F(x) = x + x^q. When q = 2^h, with h even and m = ±(q - 1)/3, the above f(t) is an o-polynomial for the Adelaide hyperoval.

^c) The Penttila-O'Keefe o-polynomial is given by:

f(t) = t⁴ + t¹⁶ + t²⁸ + η¹¹(t⁶ + t¹⁰ + t¹⁴ + t¹⁸ + t²² + t²⁶) + η²⁰(t⁸ + t²⁰) + η⁶(t¹² + t²⁴),

where η is a primitive root of GF(32) satisfying η⁵ = η² + 1.

Hyperovals in PG(2, q), q even, q ≤ 64

As the hyperovals in the Desarguesian planes of orders 2, 4 and 8 are all hyperconics we shall only examine the planes of orders 16, 32 and 64.

PG(2,16)

In (Lunelli Sce) the details of a computer search for complete arcs in small order planes carried out at the suggestion of B. Segre are given. In PG(2,16) they found a number of hyperovals which were not hyperconics. In 1975, M. Hall Jr. (Hall 1975) showed, also with considerable aid from a computer, that there were only two classes of projectively inequivalent hyperovals in this plane, the hyperconics and the hyperovals found by Lunelli and Sce. Out of the 2040 o-polynomials which give the Lunelli-Sce hyperoval, we display only one:

f(x) = x¹² + x¹⁰ + η¹¹x⁸ + x⁶ + η²x⁴ + η⁹x²,

where η is a primitive element of GF(16) satisfying η⁴ = η + 1.

In his 1975 paper Hall described a number of collineations of the plane which stabilized the Lunelli-Sce hyperoval, but did not show that they generated the full automorphism group of this hyperoval. (Payne Conklin) using properties of a related generalized quadrangle, showed that the automorphism group could be no larger than the group given by Hall. (Korchmáros 1978) independently gave a constructive proof of this result and also showed that in Desarguesian planes, the Lunelli-Sce hyperoval is the unique irregular hyperoval (non-hyperconic) admitting a transitive automorphism group (and that the only hyperconics admitting such a group are those of orders 2 and 4).

(O'Keefe Penttila) reproved Hall's classification result without the use of a computer. Their argument consists of finding an upper bound on the number of o-polynomials defined over GF(16) and then, by examining the possible automorphism groups of hyperovals in this plane, showing that if a hyperoval other than the known ones existed in this plane then the upper bound would be exceeded. (Brown Cherowitzo) provides a group-theoretic construction of the Lunelli-Sce hyperoval as the union of orbits of the group generated by the elations of PGU(3,4) considered as a subgroup of PGL(3,16). Also included in this paper is a discussion of some remarkable properties concerning the intersections of Lunelli-Sce hyperovals and hyperconics. In (Cherowitzo Penttila) it is shown that the Lunelli-Sce hyperoval is the first non-trivial member of theSubiaco family (see also (Brown Cherowitzo)). In (Cherowitzo O'Keefe) it is shown to be the first non-trivial member of the Adelaide family.

PG(2,32)

Since h = 5 is odd, a number of the known families have a representative here, but due to the small size of the plane there are some spurious equivalences, in fact, each of the Glynn type hyperovals is projectively equivalent to a translation hyperoval, and the Payne hyperoval is projectively equivalent to the Subiaco hyperoval (this does not occur in larger planes). Specifically, there are three classes of (monomial type) hyperovals, the hyperconics (f(t) = t²), proper translation hyperovals (f(t) = t⁴) and the Segre hyperovals (f(t) = t⁶).^[12] There are also classes corresponding to the Payne hyperovals and the Cherowitzo hyperovals (for more details see (Cherowitzo 1988). In (O'Keefe Penttila) the collineation groups stabilizing each of these hyperovals have been determined. Note that in the original determination of the collineation group for the Payne hyperovals the case of q = 32 had to be treated separately and relied heavily on computer results. In (O'Keefe Penttila) an alternative version of the proof is given which does not depend on computer computations.

In 1991, O'Keefe and Penttila discovered a new hyperoval in this plane by means of a detailed investigation of the divisibility properties of the orders of automorphism groups of hypothetical hyperovals (O'Keefe Penttila). One of its o-polynomials is given by:

f(x) = x⁴ + x¹⁶ + x²⁸ + η¹¹(x⁶ + x¹⁰ + x¹⁴ + x¹⁸ + x²² + x²⁶) + η²⁰(x⁸ + x²⁰) + η⁶(x¹² + x²⁴),

where η is a primitive root of GF(32) satisfying η⁵ = η² + 1. The full automorphism group of this hyperoval has order 3.

(Penttila Royle) cleverly structured an exhaustive computer search for all hyperovals in this plane. The result was that the above listing is complete, there are just six classes of hyperovals in PG(2,32).

PG(2,64)

By extending the ideas in (O'Keefe Penttila) to PG(2,64), (Penttila Pinneri) were able to search for hyperovals whose automorphism group admitted a collineation of order 5. They found two and showed that no other hyperoval exists in this plane that has such an automorphism. This settled affirmatively a long open question of B. Segre who wanted to know if there were any hyperovals in this plane besides the hyperconics. The hyperovals are:

f(x) = x⁸ + x¹² + x²⁰ + x²² + x⁴² + x⁵² + η²¹(x⁴+x¹⁰+x¹⁴+x¹⁶+x³⁰+x³⁸+x⁴⁴+x⁴⁸+x⁵⁴+x⁵⁶+x⁵⁸+x⁶⁰+x⁶²) + η⁴²(x² + x⁶ + x²⁶ + x²⁸ + x³² + x³⁶ + x⁴⁰),

which has an automorphism group of order 15, and

f(x) = x²⁴ + x³⁰ + x⁶² + η²¹(x⁴ +x⁸+x¹⁰+x¹⁴+x¹⁶+x³⁴+x³⁸ +x⁴⁰ +x⁴⁴+x⁴⁶+x⁵²+x⁵⁴+x⁵⁸+x⁶⁰) + η⁴²(x⁶+ x¹²+ x¹⁸+ x²⁰+ x²⁶+ x³² + x³⁶+ x⁴²+ x⁴⁸+x⁵⁰),

which has an automorphism group of order 60, where η is a primitive element of GF(64) satisfying η⁶ = η + 1. In (Cherowitzo Penttila) it is shown that these are Subiaco hyperovals. By refining the computer search program, (Penttila Royle) extended the search to hyperovals admitting an automorphism of order 3, and found the hyperoval:

f(x) = x⁴ + x⁸ + x¹⁴ + x³⁴ + x⁴² + x⁴⁸ + x⁶² + η²¹(x⁶+x¹⁶ +x²⁶+x²⁸+x³⁰+x³²+x⁴⁰+x⁵⁸) + η⁴²(x¹⁰ + x¹⁸ + x²⁴ + x³⁶ + x⁴⁴ + x⁵⁰ + x⁵²+ x⁶⁰),

which has an automorphism group of order 12 (η is a primitive element of GF(64) as above). This hyperoval is the first distinct Adelaide hyperoval.

Penttila and Royle (Penttila Royle) have shown that any other hyperoval in this plane would have to have a trivial automorphism group. This would mean that there would be many projectively equivalent copies of such a hyperoval, but general searches to date have found none, giving credence to the conjecture that there are no others in this plane.

Abstract ovals

Following (Bue1966), an abstract oval, also called a B-oval, of order [math]\displaystyle{ n }[/math] is a pair [math]\displaystyle{ (F,{\mathfrak G}) }[/math] where [math]\displaystyle{ F }[/math] is a set of [math]\displaystyle{ n+1 }[/math] elements, called points, and [math]\displaystyle{ {\mathfrak G} }[/math] is a set of involutions acting on [math]\displaystyle{ F }[/math] in a sharply quasi 2-transitive way, that is, for any two [math]\displaystyle{ (a_1,a_2),(b_1,b_2)\in F }[/math] with [math]\displaystyle{ a_i\neq b_j }[/math] for [math]\displaystyle{ i,j\in\{1,2\} }[/math], there exists exactly one [math]\displaystyle{ \sigma\in {\mathfrak G} }[/math] with [math]\displaystyle{ \sigma(a_1)=a_2 }[/math] and [math]\displaystyle{ \sigma(b_1)=b_2 }[/math]. Any oval embedded in a projective plane of order [math]\displaystyle{ q }[/math] might be endowed with a structure of an abstract oval of the same order. The converse is, in general, not true for [math]\displaystyle{ n\geq 8 }[/math]; indeed, for [math]\displaystyle{ n=8 }[/math] there are two abstract ovals which may not be embedded in a projective plane, see (Fa1984).

When [math]\displaystyle{ n }[/math] is even, a similar construction yields abstract hyperovals, see (Po1997): an abstract hyperoval of order [math]\displaystyle{ n }[/math] is a pair [math]\displaystyle{ (F,{\mathfrak G}) }[/math] where [math]\displaystyle{ F }[/math] is a set of [math]\displaystyle{ n+2 }[/math] elements and [math]\displaystyle{ {\mathfrak G} }[/math] is a set of fixed-point free involutions acting on [math]\displaystyle{ F }[/math] such that for any set of four distinct elements [math]\displaystyle{ a,b,c,d\in F }[/math] there is exactly one [math]\displaystyle{ \sigma\in{\mathfrak G} }[/math] with [math]\displaystyle{ \sigma(a)=b, \sigma(c)=d }[/math].

Notes

↑ In the English literature this term is usually rendered in French rather than translating it as a passing line.
↑ Dembowski 1968, p. 147
↑ Beutelspacher & Rosenbaum 1998, p. 144
↑ B. Segre: Sui k-Archi nei Piani Finiti di Caracteristica Due, Re. Math. Pures Appl. 2 (1957) pp. 289–300.
↑ Dembowski 1968, p. 51
↑ E. Hartmann: Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes. Skript, TH Darmstadt (PDF; 891 kB), p. 45.
↑ F. Buekenhout: Plans Projectifs à Ovoides Pascaliens, Arch. d. Math. Vol. XVII, 1966, pp. 89-93.
↑ J. Tits: Ovoides à Translations, Rend. Mat. 21 (1962), pp. 37–59.
↑ H. Mäurer: Ovoide mit Symmetrien an den Punkten einer Hyperebene, Abh. Math. Sem. Hamburg 45 (1976), pp. 237–244.
↑ Every pappian plane is Desarguesian, and in the finite case the converse is also true. So, for the finite planes, either descriptor is valid, but in the literature for finite planes the term "Desarguesian" predominates.
↑ Th. Buchanan: Ovale und Kegelschnitte in der komplexen projektiven Ebene, Math.-phys. Smesterberichte 26 (1979, pp. 244-260.
↑ In smaller order planes these hyperovals are not distinct from hyperconics. The proof of their existence given in (Segre Bartocci) utilizes linearized polynomials.

References

Beutelspacher, Albrecht; Rosenbaum, Ute (1998), Projective Geometry / from foundations to applications, Cambridge University Press, ISBN 978-0-521-48364-3
Buekenhout, F. (1966), "Études intrinsèque des ovales.", Rend. Mat. E Appl. 25 (5): 333–393
Brown, Julia M. N.; Cherowitzo, William E. (2000), "The Lunelli-Sce hyperoval in PG(2,16)", J. Geom. 69 (1–2): 15–36, doi:10.1007/BF01237471
Cherowitzo, William (1988), "Hyperovals in Desarguesian planes of even order", Ann. Discrete Math., Annals of Discrete Mathematics 37: 87–94, doi:10.1016/s0167-5060(08)70228-0, ISBN 978-0-444-70369-9
Cherowitzo, W. (1996), "Hyperovals in Desarguesian planes: an update", Discrete Math. 155 (1–3): 31–38, doi:10.1016/0012-365X(94)00367-R
Cherowitzo, W. (1998), "α-flocks and hyperovals", Geom. Dedicata 72 (3): 221–246, doi:10.1023/A:1005022808718
Cherowitzo, William E. (2003), "A unified construction of finite geometries associated with q-clans in characteristic 2", Adv. Geom. 3 (1): 1–21, doi:10.1515/advg.2003.002
Cherowitzo, W.; Penttila, T.; Pinneri, I.; Royle, G. F. (1996), "Flocks and ovals", Geom. Dedicata 60 (1): 17–37, doi:10.1007/BF00150865
Dembowski, Peter (1968), Finite geometries, Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 44, Berlin, New York: Springer-Verlag, ISBN 3-540-61786-8, https://archive.org/details/finitegeometries0000demb
Faina, G. (1984), "The B-ovals of order q≤8", J. Combin. Theory Ser. A 36 (3): 307–314, doi:10.1016/0097-3165(84)90038-4
Glynn, David G. (1983), "Two new sequences of ovals in finite Desarguesian planes of even order", (Combinatorial mathematics, X) Lecture Notes in Math., 1036, Berlin: Springer, pp. 217–229, doi:10.1007/BFb0071521
Hall, Marshall Jr. (1975), "Ovals in the Desarguesian plane of order 16", Ann. Mat. Pura Appl. (4) 102: 159–176, doi:10.1007/bf02410604
Hirschfeld, J. W. P. (1998), Projective geometries over finite fields (2nd ed.), New York: The Clarendon Press Oxford University Press, pp. xiv+555, ISBN 0-19-850295-8
Korchmáros, G. (1978), "Collineation groups transitive on the points of an oval [q+2-arc] of S_2,q for q even" (in Italian, English), Atti Sem. Mat. Fis. Univ. Modena 27 (1): 89–105 (1979)
Korchmáros, G. (1991), "Old and new results on ovals in finite projective planes", (Surveys in combinatorics, 1991) London Math. Soc. Lecture Note Ser., 166, Cambridge: Cambridge Univ. Press, pp. 41–72
Lunelli, L.; Sce, M. (1958) (in Italian), k-archi completi nei piani proiettivi desarguesiani di rango 8 e 16, Milan: Centro di Calcoli Numerici, Politecnico di Milano, p. 15
"A new hyperoval in PG(2,32)", J. Geom. 44 (1–2): 117–139, 1992, doi:10.1007/BF01228288
O'Keefe, Christine M.; Penttila, Tim (1991), "Hyperovals in PG(2,16)", European Journal of Combinatorics 12 (1): 51–59, doi:10.1016/s0195-6698(13)80007-8
O'Keefe, Christine M.; Penttila, Tim; Praeger, Cheryl E. (1991), "Stabilisers of hyperovals in PG(2,32)", Advances in finite geometries and designs, Chelwood Gate, 1990, New York: Oxford Univ. Press, pp. 337–351
Payne, Stanley E. (1985), "A new infinite family of generalized quadrangles", Congressus Numerantium 49: 115–128
Payne, Stanley E.; Conklin, James E. (1978), "An unusual generalized quadrangle of order sixteen", Journal of Combinatorial Theory, Series A 24 (1): 50–74, doi:10.1016/0097-3165(78)90044-4
Penttila, Tim; Pinneri, Ivano (1994), "Irregular hyperovals in PG(2,64)", J. Geom. 51 (1–2): 89–100, doi:10.1007/BF01226860
Penttila, Tim; Royle, Gordon F. (1994), "Classification of hyperovals in PG(2,32)", J. Geom. 50 (1–2): 151–158, doi:10.1007/BF01222672
Penttila, Tim; Royle, Gordon F. (1995), "On hyperovals in small projective planes", J. Geom. 54 (1–2): 91–104, doi:10.1007/BF01222857
Polster, B. (1997), "Abstract hyperovals and Hadamard designs", Australas. J. Combin. 16: 29–33
Qvist, B. (1952), "Some remarks concerning curves of the second degree in a finite plane", Ann. Acad. Sci. Fennicae. Ser. A I. Math.-Phys. 1952 (134): 27
Segre, Beniamino (1955), "Ovals in a finite projective plane", Canadian Journal of Mathematics 7: 414–416, doi:10.4153/CJM-1955-045-x, ISSN 0008-414X
Segre, Beniamino (1962), "Ovali e curve σ nei piani di Galois di caratteristica due." (in Italian), Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Nat. (8) 32: 785–790
Segre, B.; Bartocci, U. (1971), "Ovali ed altre curve nei piani di Galois di caratteristica due" (in Italian), Acta Arithmetica 18: 423–449, doi:10.4064/aa-18-1-423-449

External links

Bill Cherowitzo's Hyperoval Page

0.00

(0 votes)

Original source: https://en.wikipedia.org/wiki/Oval (projective plane). Read more

[1] In the English literature this term is usually rendered in French rather than translating it as a passing line.

[2] Dembowski 1968, p. 147

[3] Beutelspacher & Rosenbaum 1998, p. 144

[4] B. Segre: Sui k-Archi nei Piani Finiti di Caracteristica Due, Re. Math. Pures Appl. 2 (1957) pp. 289–300.

[5] Dembowski 1968, p. 51

[6] E. Hartmann: Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes. Skript, TH Darmstadt (PDF; 891 kB), p. 45.

[7] F. Buekenhout: Plans Projectifs à Ovoides Pascaliens, Arch. d. Math. Vol. XVII, 1966, pp. 89-93.

[8] J. Tits: Ovoides à Translations, Rend. Mat. 21 (1962), pp. 37–59.

[9] H. Mäurer: Ovoide mit Symmetrien an den Punkten einer Hyperebene, Abh. Math. Sem. Hamburg 45 (1976), pp. 237–244.

[10] Every pappian plane is Desarguesian, and in the finite case the converse is also true. So, for the finite planes, either descriptor is valid, but in the literature for finite planes the term "Desarguesian" predominates.

[11] Th. Buchanan: Ovale und Kegelschnitte in der komplexen projektiven Ebene, Math.-phys. Smesterberichte 26 (1979, pp. 244-260.

[12] In smaller order planes these hyperovals are not distinct from hyperconics. The proof of their existence given in (Segre Bartocci) utilizes linearized polynomials.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

Oval (projective plane)

Contents

Definition of an oval