Parallelogram of force

Main page: Vector addition

The parallelogram of forces is a method for solving (or visualizing) the results of applying two forces to an object.

Figure 1: Parallelogram construction for adding vectors

When more than two forces are involved, the geometry is no longer parallelogrammatic, but the same principles apply. Forces, being vectors are observed to obey the laws of vector addition, and so the overall (resultant) force due to the application of a number of forces can be found geometrically by drawing vector arrows for each force. For example, see Figure 1. This construction has the same result as moving F₂ so its tail coincides with the head of F₁, and taking the net force as the vector joining the tail of F₁ to the head of F₂. This procedure can be repeated to add F₃ to the resultant F₁ + F₂, and so forth. Alternatively, a polygon of forces can be used.

Newton's proof

Figure 2: Parallelogram of velocity

Preliminary: the parallelogram of velocity

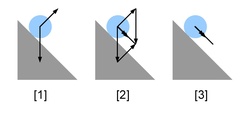
Suppose a particle moves at a uniform rate along a line from A to B (Figure 2) in a given time (say, one second), while in the same time, the line AB moves uniformly from its position at AB to a position at DC, remaining parallel to its original orientation throughout. Accounting for both motions, the particle traces the line AC. Because a displacement in a given time is a measure of velocity, the length of AB is a measure of the particle's velocity along AB, the length of AD is a measure of the line's velocity along AD, and the length of AC is a measure of the particle's velocity along AC. The particle's motion is the same as if it had moved with a single velocity along AC.^[1]

Newton's proof of the parallelogram of force

Suppose two forces act on a particle at the origin (the "tails" of the vectors) of Figure 1. Let the lengths of the vectors F₁ and F₂ represent the velocities the two forces could produce in the particle by acting for a given time, and let the direction of each represent the direction in which they act. Each force acts independently and will produce its particular velocity whether the other force acts or not. At the end of the given time, the particle has both velocities. By the above proof, they are equivalent to a single velocity, F_net. By Newton's second law, this vector is also a measure of the force which would produce that velocity, thus the two forces are equivalent to a single force.^[2]

Using a parallelogram to add the forces acting on a particle on a smooth slope. We find, as we'd expect, that the resultant (double headed arrow) force acts down the slope, which will cause the particle to accelerate in that direction.

Bernoulli's proof for perpendicular vectors

We model forces as Euclidean vectors or members of [math]\displaystyle{ \mathbb{R}^2 }[/math]. Our first assumption is that the resultant of two forces is in fact another force, so that for any two forces [math]\displaystyle{ \mathbf{F}, \mathbf{G} \in \mathbb{R}^2 }[/math] there is another force [math]\displaystyle{ \mathbf{F} \oplus \mathbf{G} \in \mathbb{R}^2 }[/math]. Our final assumption is that the resultant of two forces doesn't change when rotated. If [math]\displaystyle{ R: \mathbb{R}^2\to \mathbb{R}^2 }[/math] is any rotation (any orthogonal map for the usual vector space structure of [math]\displaystyle{ \mathbb{R}^2 }[/math] with [math]\displaystyle{ \det R = 1 }[/math]), then for all forces [math]\displaystyle{ \mathbf{F}, \mathbf{G}\in \mathbb{R}^2 }[/math]

[math]\displaystyle{ R \left( \mathbf{F} \oplus \mathbf{G} \right) = R \left(\mathbf{F} \right) \oplus R \left(\mathbf{G} \right) }[/math]

Consider two perpendicular forces [math]\displaystyle{ \mathbf{F}_1 }[/math] of length [math]\displaystyle{ a }[/math] and [math]\displaystyle{ \mathbf{F}_2 }[/math] of length [math]\displaystyle{ b }[/math], with [math]\displaystyle{ x }[/math] being the length of [math]\displaystyle{ \mathbf{F}_1 \oplus \mathbf{F}_2 }[/math]. Let [math]\displaystyle{ \mathbf{G}_1 := \tfrac{a^2}{x^2} \left( \mathbf{F}_1\oplus \mathbf{F}_2 \right) }[/math] and [math]\displaystyle{ \mathbf{G}_2 := \tfrac{a}{x} R(\mathbf{F}_2) }[/math], where [math]\displaystyle{ R }[/math] is the rotation between [math]\displaystyle{ \mathbf{F}_1 }[/math] and [math]\displaystyle{ \mathbf{F}_1 \oplus \mathbf{F}_2 }[/math], so [math]\displaystyle{ \mathbf{G_1} = \tfrac{a}{x} R \left(\mathbf{F}_1 \right) }[/math]. Under the invariance of the rotation, we get

[math]\displaystyle{ \mathbf{F}_1=\frac{x}{a}R^{-1} \left(\mathbf{G}_1 \right) = \frac{a}{x}R^{-1} \left(\mathbf{F}_1\oplus\mathbf{F}_2 \right)=\frac{a}{x}R^{-1} \left(\mathbf{F}_1 \right)\oplus\frac{a}{x}R^{-1} \left(\mathbf{F}_2 \right)=\mathbf{G}_1 \oplus \mathbf{G}_2 }[/math]

Similarly, consider two more forces [math]\displaystyle{ \mathbf{H}_1 := -\mathbf{G}_2 }[/math] and [math]\displaystyle{ \mathbf{H}_2 := \tfrac{b^2}{x^2} \left( \mathbf{F}_1 \oplus \mathbf{F}_2 \right) }[/math]. Let [math]\displaystyle{ T }[/math] be the rotation from [math]\displaystyle{ \mathbf{F}_1 }[/math] to [math]\displaystyle{ \mathbf{H}_1 }[/math]: [math]\displaystyle{ \mathbf{H}_1 = \tfrac{b}{x} T\left(\mathbf{F}_1\right) }[/math], which by inspection makes [math]\displaystyle{ \mathbf{H}_2 =\tfrac{b}{x} T\left(\mathbf{F}_2\right) }[/math].

[math]\displaystyle{ \mathbf{F}_2 = \frac{x}{b}T^{-1}\left(\mathbf{H}_2\right) = \frac{b}{x}T^{-1}\left(\mathbf{F}_1\oplus\mathbf{F}_2\right)=\frac{b}{x}T^{-1}\left(\mathbf{F}_1\right)\oplus\frac{b}{x}T^{-1}\left(\mathbf{F}_2\right)=\mathbf{H}_1\oplus\mathbf{H_2} }[/math]

Applying these two equations

[math]\displaystyle{ \mathbf{F}_1\oplus \mathbf{F}_2 = \left(\mathbf{G}_1 \oplus \mathbf{G}_2 \right) \oplus \left(\mathbf{H}_1\oplus \mathbf{H_2} \right) = \left(\mathbf{G}_1 \oplus \mathbf{G}_2 \right) \oplus \left(-\mathbf{G}_2\oplus \mathbf{H}_2 \right) = \mathbf{G}_1 \oplus \mathbf{H}_2 }[/math]

Since [math]\displaystyle{ \mathbf{G}_1 }[/math] and [math]\displaystyle{ \mathbf{H}_2 }[/math] both lie along [math]\displaystyle{ \mathbf{F}_1 \oplus \mathbf{F}_2 }[/math], their lengths are equal [math]\displaystyle{ x= \left|\mathbf{F}_1 \oplus \mathbf{F}_2 \right| = \left|\mathbf{G}_1 \oplus \mathbf{H}_2 \right|= \tfrac{a^2}{x}+\tfrac{b^2}{x} }[/math]

[math]\displaystyle{ x = \sqrt{a^2+b^2} }[/math]

which implies that [math]\displaystyle{ \mathbf{F}_1 \oplus \mathbf{F}_2 = a \mathbf{e}_1 \oplus b \mathbf{e}_2 }[/math] has length [math]\displaystyle{ \sqrt{a^2+b^2} }[/math], which is the length of [math]\displaystyle{ a \mathbf{e}_1 + b \mathbf{e}_2 }[/math]. Thus for the case where [math]\displaystyle{ \mathbf{F}_1 }[/math] and [math]\displaystyle{ \mathbf{F}_2 }[/math] are perpendicular, [math]\displaystyle{ \mathbf{F}_1 \oplus \mathbf{F}_2 = \mathbf{F}_1 + \mathbf{F}_2 }[/math]. However, when combining our two sets of auxiliary forces we used the associativity of [math]\displaystyle{ \oplus }[/math]. Using this additional assumption, we will form an additional proof below.^{[3] [4]}

Algebraic proof of the parallelogram of force

We model forces as Euclidean vectors or members of [math]\displaystyle{ \mathbb{R}^2 }[/math]. Our first assumption is that the resultant of two forces is in fact another force, so that for any two forces [math]\displaystyle{ \mathbf{F}, \mathbf{G} \in \mathbb{R}^2 }[/math] there is another force [math]\displaystyle{ \mathbf{F} \oplus \mathbf{G} \in \mathbb{R}^2 }[/math]. We assume commutativity, as these are forces being applied concurrently, so the order shouldn't matter [math]\displaystyle{ \mathbf{F} \oplus \mathbf{G} = \mathbf{G} \oplus \mathbf{F} }[/math].

Consider the map [math]\displaystyle{ (a,b) = a \mathbf{e}_1 + b \mathbf{e}_2 \mapsto a \mathbf{e}_1 \oplus b \mathbf{e}_2 }[/math]

If [math]\displaystyle{ \oplus }[/math] is associative, then this map will be linear. Since it also sends [math]\displaystyle{ \mathbf{e}_1 }[/math] to [math]\displaystyle{ \mathbf{e}_1 }[/math] and [math]\displaystyle{ \mathbf{e}_2 }[/math] to [math]\displaystyle{ \mathbf{e}_2 }[/math], it must also be the identity map. Thus [math]\displaystyle{ \oplus }[/math] must be equivalent to the normal vector addition operator.^[3][5]

Controversy

The mathematical proof of the parallelogram of force is not generally accepted to be mathematically valid. Various proofs were developed (chiefly Duchayla's and Poisson's), and these also caused objections. That the parallelogram of force was true was not questioned, but why it was true. Today the parallelogram of force is accepted as an empirical fact, non-reducible to Newton's first principles. ^{[3] [6]}

See also

• Newton's Mathematical Principles of Natural Philosophy, Axioms or Laws of Motion, Corollary I, at Wikisource
• Vector (geometric)
• Net force

References

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Parallelogram of force. Read more