Paxos (computer science)

Short description: Family of protocols for solving consensus

Paxos is a family of protocols for solving consensus in a network of unreliable or fallible processors. Consensus is the process of agreeing on one result among a group of participants. This problem becomes difficult when the participants or their communications may experience failures.^[1]

Consensus protocols are the basis for the state machine replication approach to distributed computing, as suggested by Leslie Lamport^[2] and surveyed by Fred Schneider.^[3] State machine replication is a technique for converting an algorithm into a fault-tolerant, distributed implementation. Ad-hoc techniques may leave important cases of failures unresolved. The principled approach proposed by Lamport et al. ensures all cases are handled safely.

The Paxos protocol was first submitted in 1989 and named after a fictional legislative consensus system used on the Paxos island in Greece, where Lamport wrote that the parliament had to function "even though legislators continually wandered in and out of the parliamentary Chamber".^[4] It was later published as a journal article in 1998.^[5]

The Paxos family of protocols includes a spectrum of trade-offs between the number of processors, number of message delays before learning the agreed value, the activity level of individual participants, number of messages sent, and types of failures. Although no deterministic fault-tolerant consensus protocol can guarantee progress in an asynchronous network (a result proved in a paper by Fischer, Lynch and Paterson^[6]), Paxos guarantees safety (consistency), and the conditions that could prevent it from making progress are difficult to provoke.

Paxos is usually used where durability is required (for example, to replicate a file or a database), in which the amount of durable state could be large. The protocol attempts to make progress even during periods when some bounded number of replicas are unresponsive. There is also a mechanism to drop a permanently failed replica or to add a new replica.

History

The topic predates the protocol. In 1988, Lynch, Dwork and Stockmeyer had demonstrated ^[7] the solvability of consensus in a broad family of "partially synchronous" systems. Paxos has strong similarities to a protocol used for agreement in "viewstamped replication", first published by Oki and Liskov in 1988, in the context of distributed transactions.^[8] Notwithstanding this prior work, Paxos offered a particularly elegant formalism, and included one of the earliest proofs of safety for a fault-tolerant distributed consensus protocol.

Reconfigurable state machines have strong ties to prior work on reliable group multicast protocols that support dynamic group membership, for example Birman's work in 1985 and 1987 on the virtually synchronous gbcast^[9] protocol. However, gbcast is unusual in supporting durability and addressing partitioning failures. Most reliable multicast protocols lack these properties, which are required for implementations of the state machine replication model. This point is elaborated in a paper by Lamport, Malkhi and Zhou.^[10]

Paxos protocols are members of a theoretical class of solutions to a problem formalized as uniform agreement with crash failures. Lower bounds for this problem have been proved by Keidar and Shraer.^[11] Derecho,^[12] a C++ software library for cloud-scale state machine replication, offers a Paxos protocol that has been integrated with self-managed virtually synchronous membership. This protocol matches the Keidar and Shraer optimality bounds, and maps efficiently to modern remote DMA (RDMA) datacenter hardware (but uses TCP if RDMA is not available).

Assumptions

In order to simplify the presentation of Paxos, the following assumptions and definitions are made explicit. Techniques to broaden the applicability are known in the literature, and are not covered in this article.

Processors

Processors operate at arbitrary speed.
Processors may experience failures.
Processors with stable storage may re-join the protocol after failures (following a crash-recovery failure model).
Processors do not collude, lie, or otherwise attempt to subvert the protocol. (That is, Byzantine failures don't occur. See Byzantine Paxos for a solution that tolerates failures that arise from arbitrary/malicious behavior of the processes.)

Network

Processors can send messages to any other processor.
Messages are sent asynchronously and may take arbitrarily long to deliver.
Messages may be lost, reordered, or duplicated.
Messages are delivered without corruption. (That is, Byzantine failures don't occur. See Byzantine Paxos for a solution which tolerates corrupted messages that arise from arbitrary/malicious behavior of the messaging channels.)

Number of processors

In general, a consensus algorithm can make progress using [math]\displaystyle{ n=2F+1 }[/math] processors, despite the simultaneous failure of any [math]\displaystyle{ F }[/math] processors:^[13] in other words, the number of non-faulty processes must be strictly greater than the number of faulty processes. However, using reconfiguration, a protocol may be employed which survives any number of total failures as long as no more than F fail simultaneously. For Paxos protocols, these reconfigurations can be handled as separate configurations.^[14]

Safety and liveness properties

In order to guarantee safety (also called "consistency"), Paxos defines three properties and ensures the first two are always held, regardless of the pattern of failures:

Validity (or non-triviality): Only proposed values can be chosen and learned.^[15]
Agreement (or consistency, or safety): No two distinct learners can learn different values (or there can't be more than one decided value)^[15]^[16]
Termination (or liveness): If value C has been proposed, then eventually learner L will learn some value (if sufficient processors remain non-faulty).^[16]

Note that Paxos is not guaranteed to terminate, and thus does not have the liveness property. This is supported by the Fischer Lynch Paterson impossibility result (FLP)^[6] which states that a consistency protocol can only have two of safety, liveness, and fault tolerance. As Paxos's point is to ensure fault tolerance and it guarantees safety, it cannot also guarantee liveness.

Typical deployment

In most deployments of Paxos, each participating process acts in three roles; Proposer, Acceptor and Learner.^[17] This reduces the message complexity significantly, without sacrificing correctness:

“

In Paxos, clients send commands to a leader. During normal operation, the leader receives a client's command, assigns it a new command number [math]\displaystyle{ i }[/math], and then begins the [math]\displaystyle{ i }[/math]^th instance of the consensus algorithm by sending messages to a set of acceptor processes.^[16]

”

By merging roles, the protocol "collapses" into an efficient client-master-replica style deployment, typical of the database community.^[18] The benefit of the Paxos protocols (including implementations with merged roles) is the guarantee of its safety properties.

A typical implementation's message flow is covered in the section Multi-Paxos.

Basic Paxos

This protocol is the most basic of the Paxos family. Each "instance" (or "execution") of the basic Paxos protocol decides on a single output value. The protocol proceeds over several rounds. A successful round has 2 phases: phase 1 (which is divided into parts a and b) and phase 2 (which is divided into parts a and b). See below the description of the phases. Remember that we assume an asynchronous model, so e.g. a processor may be in one phase while another processor may be in another.

Phase 1

Phase 1a: Prepare

A Proposer creates a message, which we call a "Prepare", identified with a number n. Note that n is not the value to be proposed and maybe agreed on, but just a number which uniquely identifies this initial message by the proposer (to be sent to the acceptors). The number n must be greater than any number used in any of the previous Prepare messages by this Proposer. Then, it sends the Prepare message containing n to at least a Quorum of Acceptors. Note that the Prepare message only contains the number n (that is, it does not have to contain e.g. the proposed value, often denoted by v). The Proposer decides who is in the Quorum. A Proposer should not initiate Paxos if it cannot communicate with at least a Quorum of Acceptors.

Phase 1b: Promise

Any of the Acceptors waits for a Prepare message from any of the Proposers. If an Acceptor receives a Prepare message, the Acceptor must look at the identifier number n of the just received Prepare message. There are two cases.

If n is higher than every previous proposal number received, from any of the Proposers, by the Acceptor, then the Acceptor must return a message, which we call a "Promise", to the Proposer, to ignore all future proposals having a number less than n. If the Acceptor accepted a proposal at some point in the past, it must include the previous proposal number, say m, and the corresponding accepted value, say w, in its response to the Proposer.

Otherwise (that is, n is less than or equal to any previous proposal number received from any Proposer by the Acceptor) the Acceptor can ignore the received proposal. It does not have to answer in this case for Paxos to work. However, for the sake of optimization, sending a denial (Nack) response would tell the Proposer that it can stop its attempt to create consensus with proposal n.

Phase 2

Phase 2a: Accept

If a Proposer receives Promises from a Quorum of Acceptors, it needs to set a value v to its proposal. If any Acceptors had previously accepted any proposal, then they'll have sent their values to the Proposer, who now must set the value of its proposal, v, to the value associated with the highest proposal number reported by the Acceptors, let's call it z. If none of the Acceptors had accepted a proposal up to this point, then the Proposer may choose the value it originally wanted to propose, say x.^[19]

The Proposer sends an Accept message, (n, v), to a Quorum of Acceptors with the chosen value for its proposal, v, and the proposal number n (which is the same as the number contained in the Prepare message previously sent to the Acceptors). So, the Accept message is either (n, v=z) or, in case none of the Acceptors previously accepted a value, (n, v=x).

This Accept message should be interpreted as a "request", as in "Accept this proposal, please!".

Phase 2b: Accepted

If an Acceptor receives an Accept message, (n, v), from a Proposer, it must accept it if and only if it has not already promised (in Phase 1b of the Paxos protocol) to only consider proposals having an identifier greater than n.

If the Acceptor has not already promised (in Phase 1b) to only consider proposals having an identifier greater than n, it should register the value v (of the just received Accept message) as the accepted value (of the Protocol), and send an Accepted message to the Proposer and every Learner (which can typically be the Proposers themselves. Learners will learn the decided value ONLY AFTER receiving Accepted messages from a majority of acceptors, which means, NOT after receiving just the FIRST Accept message).

Else, it can ignore the Accept message or request.

Note that consensus is achieved when a majority of Acceptors accept the same identifier number (rather than the same value). Because each identifier is unique to a Proposer and only one value may be proposed per identifier, all Acceptors that accept the same identifier thereby accept the same value. These facts result in a few counter-intuitive scenarios that do not impact correctness: Acceptors can accept multiple values, a value may achieve a majority across Acceptors (with different identifiers) only to later be changed, and Acceptors may continue to accept proposals after an identifier has achieved a majority. However, the Paxos protocol guarantees that consensus is permanent and the chosen value is immutable.

When rounds fail

Rounds fail when multiple Proposers send conflicting Prepare messages, or when the Proposer does not receive a Quorum of responses (Promise or Accepted). In these cases, another round must be started with a higher proposal number.

Paxos can be used to select a leader

Notice that a Proposer in Paxos could propose "I am the leader," (or, for example, "Proposer X is the leader").^[20] Because of the agreement and validity guarantees of Paxos, if accepted by a Quorum, then the Proposer is now known to be the leader to all other nodes. This satisfies the needs of leader election^[21] because there is a single node believing it is the leader and a single node known to be the leader at all times.

Graphic representation of the flow of messages in the basic Paxos

The following diagrams represent several cases/situations of the application of the Basic Paxos protocol. Some cases show how the Basic Paxos protocol copes with the failure of certain (redundant) components of the distributed system.

Note that the values returned in the Promise message are "null" the first time a proposal is made (since no Acceptor has accepted a value before in this round).

Basic Paxos without failures

In the diagram below, there is 1 Client, 1 Proposer, 3 Acceptors (i.e. the Quorum size is 3) and 2 Learners (represented by the 2 vertical lines). This diagram represents the case of a first round, which is successful (i.e. no process in the network fails).

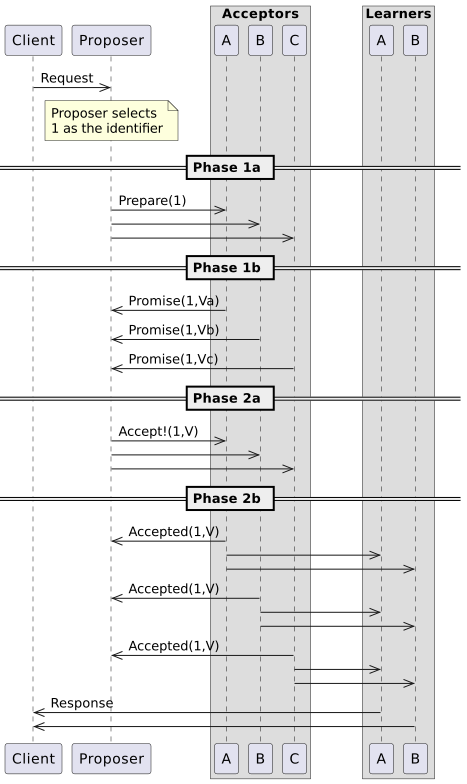
Here, V is the last of (Va, Vb, Vc).

Error cases in basic Paxos

The simplest error cases are the failure of an Acceptor (when a Quorum of Acceptors remains alive) and failure of a redundant Learner. In these cases, the protocol requires no "recovery" (i.e. it still succeeds): no additional rounds or messages are required, as shown below (in the next two diagrams/cases).

Basic Paxos when an Acceptor fails

In the following diagram, one of the Acceptors in the Quorum fails, so the Quorum size becomes 2. In this case, the Basic Paxos protocol still succeeds.

Client   Proposer      Acceptor     Learner
   |         |          |  |  |       |  |
   X-------->|          |  |  |       |  |  Request
   |         X--------->|->|->|       |  |  Prepare(1)
   |         |          |  |  !       |  |  !! FAIL !!
   |         |<---------X--X          |  |  Promise(1,{Va, Vb, null})
   |         X--------->|->|          |  |  Accept!(1,V)
   |         |<---------X--X--------->|->|  Accepted(1,V)
   |<---------------------------------X--X  Response
   |         |          |  |          |  |

Basic Paxos when a redundant learner fails

In the following case, one of the (redundant) Learners fails, but the Basic Paxos protocol still succeeds.

Client Proposer         Acceptor     Learner
   |         |          |  |  |       |  |
   X-------->|          |  |  |       |  |  Request
   |         X--------->|->|->|       |  |  Prepare(1)
   |         |<---------X--X--X       |  |  Promise(1,{Va,Vb,Vc})
   |         X--------->|->|->|       |  |  Accept!(1,V)
   |         |<---------X--X--X------>|->|  Accepted(1,V)
   |         |          |  |  |       |  !  !! FAIL !!
   |<---------------------------------X     Response
   |         |          |  |  |       |

Basic Paxos when a Proposer fails

In this case, a Proposer fails after proposing a value, but before the agreement is reached. Specifically, it fails in the middle of the Accept message, so only one Acceptor of the Quorum receives the value. Meanwhile, a new Leader (a Proposer) is elected (but this is not shown in detail). Note that there are 2 rounds in this case (rounds proceed vertically, from the top to the bottom).

Client  Proposer        Acceptor     Learner
   |      |             |  |  |       |  |
   X----->|             |  |  |       |  |  Request
   |      X------------>|->|->|       |  |  Prepare(1)
   |      |<------------X--X--X       |  |  Promise(1,{Va, Vb, Vc})
   |      |             |  |  |       |  |
   |      |             |  |  |       |  |  !! Leader fails during broadcast !!
   |      X------------>|  |  |       |  |  Accept!(1,V)
   |      !             |  |  |       |  |
   |         |          |  |  |       |  |  !! NEW LEADER !!
   |         X--------->|->|->|       |  |  Prepare(2)
   |         |<---------X--X--X       |  |  Promise(2,{V, null, null})
   |         X--------->|->|->|       |  |  Accept!(2,V)
   |         |<---------X--X--X------>|->|  Accepted(2,V)
   |<---------------------------------X--X  Response
   |         |          |  |  |       |  |

Basic Paxos when multiple Proposers conflict

The most complex case is when multiple Proposers believe themselves to be Leaders. For instance, the current leader may fail and later recover, but the other Proposers have already re-selected a new leader. The recovered leader has not learned this yet and attempts to begin one round in conflict with the current leader. In the diagram below, 4 unsuccessful rounds are shown, but there could be more (as suggested at the bottom of the diagram).

Client   Proposer       Acceptor     Learner
   |      |             |  |  |       |  |
   X----->|             |  |  |       |  |  Request
   |      X------------>|->|->|       |  |  Prepare(1)
   |      |<------------X--X--X       |  |  Promise(1,{null,null,null})
   |      !             |  |  |       |  |  !! LEADER FAILS
   |         |          |  |  |       |  |  !! NEW LEADER (knows last number was 1)
   |         X--------->|->|->|       |  |  Prepare(2)
   |         |<---------X--X--X       |  |  Promise(2,{null,null,null})
   |      |  |          |  |  |       |  |  !! OLD LEADER recovers
   |      |  |          |  |  |       |  |  !! OLD LEADER tries 2, denied
   |      X------------>|->|->|       |  |  Prepare(2)
   |      |<------------X--X--X       |  |  Nack(2)
   |      |  |          |  |  |       |  |  !! OLD LEADER tries 3
   |      X------------>|->|->|       |  |  Prepare(3)
   |      |<------------X--X--X       |  |  Promise(3,{null,null,null})
   |      |  |          |  |  |       |  |  !! NEW LEADER proposes, denied
   |      |  X--------->|->|->|       |  |  Accept!(2,Va)
   |      |  |<---------X--X--X       |  |  Nack(3)
   |      |  |          |  |  |       |  |  !! NEW LEADER tries 4
   |      |  X--------->|->|->|       |  |  Prepare(4)
   |      |  |<---------X--X--X       |  |  Promise(4,{null,null,null})
   |      |  |          |  |  |       |  |  !! OLD LEADER proposes, denied
   |      X------------>|->|->|       |  |  Accept!(3,Vb)
   |      |<------------X--X--X       |  |  Nack(4)
   |      |  |          |  |  |       |  |  ... and so on ...

Basic Paxos where an Acceptor accepts Two Different Values

In the following case, one Proposer achieves acceptance of value V1 by one Acceptor before failing. A new Proposer prepares the Acceptors that never accepted V1, allowing it to propose V2. Then V2 is accepted by all Acceptors, including the one that initially accepted V1.

Proposer    Acceptor     Learner
 |  |       |  |  |       |  |
 X--------->|->|->|       |  |  Prepare(1)
 |<---------X--X--X       |  |  Promise(1,{null,null,null})
 x--------->|  |  |       |  |  Accept!(1,V1)
 |  |       X------------>|->|  Accepted(1,V1)
 !  |       |  |  |       |  |  !! FAIL !!
    |       |  |  |       |  |
    X--------->|->|       |  |  Prepare(2)
    |<---------X--X       |  |  Promise(2,{null,null})
    X------>|->|->|       |  |  Accept!(2,V2)
    |<------X--X--X------>|->|  Accepted(2,V2)
    |       |  |  |       |  |

Basic Paxos where a multi-identifier majority is insufficient

In the following case, one Proposer achieves acceptance of value V1 of one Acceptor before failing. A new Proposer prepares the Acceptors that never accepted V1, allowing it to propose V2. This Proposer is able to get one Acceptor to accept V2 before failing. A new Proposer finds a majority that includes the Acceptor that has accepted V1, and must propose it. The Proposer manages to get two Acceptors to accept it before failing. At this point, three Acceptors have accepted V1, but not for the same identifier. Finally, a new Proposer prepares the majority that has not seen the largest accepted identifier. The value associated with the largest identifier in that majority is V2, so it must propose it. This Proposer then gets all Acceptors to accept V2, achieving consensus.

  Proposer           Acceptor        Learner
 |  |  |  |       |  |  |  |  |       |  |
 X--------------->|->|->|->|->|       |  |  Prepare(1)
 |<---------------X--X--X--X--X       |  |  Promise(1,{null,null,null,null,null})
 x--------------->|  |  |  |  |       |  |  Accept!(1,V1)
 |  |  |  |       X------------------>|->|  Accepted(1,V1)
 !  |  |  |       |  |  |  |  |       |  |  !! FAIL !!
    |  |  |       |  |  |  |  |       |  |
    X--------------->|->|->|->|       |  |  Prepare(2)
    |<---------------X--X--X--X       |  |  Promise(2,{null,null,null,null})
    X--------------->|  |  |  |       |  |  Accept!(2,V2)
    |  |  |       |  X--------------->|->|  Accepted(2,V2)
    !  |  |       |  |  |  |  |       |  |  !! FAIL !!
       |  |       |  |  |  |  |       |  | 
       X--------->|---->|->|->|       |  |  Prepare(3)
       |<---------X-----X--X--X       |  |  Promise(3,{V1,null,null,null})
       X--------------->|->|  |       |  |  Accept!(3,V1)
       |  |       |  |  X--X--------->|->|  Accepted(3,V1)
       !  |       |  |  |  |  |       |  |  !! FAIL !!
          |       |  |  |  |  |       |  |
          X------>|->|------->|       |  |  Prepare(4)
          |<------X--X--|--|--X       |  |  Promise(4,{V1(1),V2(2),null})
          X------>|->|->|->|->|       |  |  Accept!(4,V2)
          |       X--X--X--X--X------>|->|  Accepted(4,V2)

Basic Paxos where new Proposers cannot change an existing consensus

In the following case, one Proposer achieves acceptance of value V1 of two Acceptors before failing. A new Proposer may start another round, but it is now impossible for that proposer to prepare a majority that doesn't include at least one Acceptor that has accepted V1. As such, even though the Proposer doesn't see the existing consensus, the Proposer's only option is to propose the value already agreed upon. New Proposers can continually increase the identifier to restart the process, but the consensus can never be changed.

Proposer    Acceptor     Learner
 |  |       |  |  |       |  |
 X--------->|->|->|       |  |  Prepare(1)
 |<---------X--X--X       |  |  Promise(1,{null,null,null})
 x--------->|->|  |       |  |  Accept!(1,V1)
 |  |       X--X--------->|->|  Accepted(1,V1)
 !  |       |  |  |       |  |  !! FAIL !!
    |       |  |  |       |  |
    X--------->|->|       |  |  Prepare(2)
    |<---------X--X       |  |  Promise(2,{V1,null})
    X------>|->|->|       |  |  Accept!(2,V1)
    |<------X--X--X------>|->|  Accepted(2,V1)
    |       |  |  |       |  |

Multi-Paxos

A typical deployment of Paxos requires a continuous stream of agreed values acting as commands to a distributed state machine. If each command is the result of a single instance of the Basic Paxos protocol, a significant amount of overhead would result.

If the leader is relatively stable, phase 1 becomes unnecessary. Thus, it is possible to skip phase 1 for future instances of the protocol with the same leader.

To achieve this, the round number I is included along with each value which is incremented in each round by the same Leader. Multi-Paxos reduces the failure-free message delay (proposal to learning) from 4 delays to 2 delays.

Graphic representation of the flow of messages in the Multi-Paxos

Multi-Paxos without failures

In the following diagram, only one instance (or "execution") of the basic Paxos protocol, with an initial Leader (a Proposer), is shown. Note that a Multi-Paxos consists of several instances of the basic Paxos protocol.

Client   Proposer      Acceptor     Learner
   |         |          |  |  |       |  | --- First Request ---
   X-------->|          |  |  |       |  |  Request
   |         X--------->|->|->|       |  |  Prepare(N)
   |         |<---------X--X--X       |  |  Promise(N,I,{Va,Vb,Vc})
   |         X--------->|->|->|       |  |  Accept!(N,I,V)
   |         |<---------X--X--X------>|->|  Accepted(N,I,V)
   |<---------------------------------X--X  Response
   |         |          |  |  |       |  |

where V = last of (Va, Vb, Vc).

Multi-Paxos when phase 1 can be skipped

In this case, subsequent instances of the basic Paxos protocol (represented by I+1) use the same leader, so the phase 1 (of these subsequent instances of the basic Paxos protocol), which consist of the Prepare and Promise sub-phases, is skipped. Note that the Leader should be stable, i.e. it should not crash or change.

Client   Proposer       Acceptor     Learner
   |         |          |  |  |       |  |  --- Following Requests ---
   X-------->|          |  |  |       |  |  Request
   |         X--------->|->|->|       |  |  Accept!(N,I+1,W)
   |         |<---------X--X--X------>|->|  Accepted(N,I+1,W)
   |<---------------------------------X--X  Response
   |         |          |  |  |       |  |

Multi-Paxos when roles are collapsed

A common deployment of the Multi-Paxos consists in collapsing the role of the Proposers, Acceptors and Learners to "Servers". So, in the end, there are only "Clients" and "Servers".

The following diagram represents the first "instance" of a basic Paxos protocol, when the roles of the Proposer, Acceptor and Learner are collapsed to a single role, called the "Server".

Client      Servers
   |         |  |  | --- First Request ---
   X-------->|  |  |  Request
   |         X->|->|  Prepare(N)
   |         |<-X--X  Promise(N, I, {Va, Vb})
   |         X->|->|  Accept!(N, I, Vn)
   |         X<>X<>X  Accepted(N, I)
   |<--------X  |  |  Response
   |         |  |  |

Multi-Paxos when roles are collapsed and the leader is steady

In the subsequent instances of the basic Paxos protocol, with the same leader as in the previous instances of the basic Paxos protocol, the phase 1 can be skipped.

Client      Servers
   X-------->|  |  |  Request
   |         X->|->|  Accept!(N,I+1,W)
   |         X<>X<>X  Accepted(N,I+1)
   |<--------X  |  |  Response
   |         |  |  |

Optimisations

A number of optimisations can be performed to reduce the number of exchanged messages, to improve the performance of the protocol, etc. A few of these optimisations are reported below.

"We can save messages at the cost of an extra message delay by having a single distinguished learner that informs the other learners when it finds out that a value has been chosen. Acceptors then send Accepted messages only to the distinguished learner. In most applications, the roles of leader and distinguished learner are performed by the same processor.^[22]

"A leader can send its Prepare and Accept! messages just to a quorum of acceptors. As long as all acceptors in that quorum are working and can communicate with the leader and the learners, there is no need for acceptors not in the quorum to do anything.^[22]

"Acceptors do not care what value is chosen. They simply respond to Prepare and Accept! messages to ensure that, despite failures, only a single value can be chosen. However, if an acceptor does learn what value has been chosen, it can store the value in stable storage and erase any other information it has saved there. If the acceptor later receives a Prepare or Accept! message, instead of performing its Phase1b or Phase2b action, it can simply inform the leader of the chosen value.^[22]

"Instead of sending the value v, the leader can send a hash of v to some acceptors in its Accept! messages. A learner will learn that v is chosen if it receives Accepted messages for either v or its hash from a quorum of acceptors, and at least one of those messages contains v rather than its hash. However, a leader could receive Promise messages that tell it the hash of a value v that it must use in its Phase2a action without telling it the actual value of v. If that happens, the leader cannot execute its Phase2a action until it communicates with some process that knows v."^[22]

"A proposer can send its proposal only to the leader rather than to all coordinators. However, this requires that the result of the leader-selection algorithm be broadcast to the proposers, which might be expensive. So, it might be better to let the proposer send its proposal to all coordinators. (In that case, only the coordinators themselves need to know who the leader is.)^[15]

"Instead of each acceptor sending Accepted messages to each learner, acceptors can send their Accepted messages to the leader and the leader can inform the learners when a value has been chosen. However, this adds an extra message delay.^[15]

"Finally, observe that phase 1 is unnecessary for round 1 .. The leader of round 1 can begin the round by sending an Accept! message with any proposed value."^[15]

Cheap Paxos

Cheap Paxos extends Basic Paxos to tolerate F failures with F+1 main processors and F auxiliary processors by dynamically reconfiguring after each failure.

This reduction in processor requirements comes at the expense of liveness; if too many main processors fail in a short time, the system must halt until the auxiliary processors can reconfigure the system. During stable periods, the auxiliary processors take no part in the protocol.

"With only two processors p and q, one processor cannot distinguish failure of the other processor from failure of the communication medium. A third processor is needed. However, that third processor does not have to participate in choosing the sequence of commands. It must take action only in case p or q fails, after which it does nothing while either p or q continues to operate the system by itself. The third processor can therefore be a small/slow/cheap one, or a processor primarily devoted to other tasks."^[22]

Message flow: Cheap Multi-Paxos

An example involving three main acceptors, one auxiliary acceptor and quorum size of three, showing failure of one main processor and subsequent reconfiguration:

            {  Acceptors  }
Proposer     Main       Aux    Learner
|            |  |  |     |       |  -- Phase 2 --
X----------->|->|->|     |       |  Accept!(N,I,V)
|            |  |  !     |       |  --- FAIL! ---
|<-----------X--X--------------->|  Accepted(N,I,V)
|            |  |        |       |  -- Failure detected (only 2 accepted) --
X----------->|->|------->|       |  Accept!(N,I,V)  (re-transmit, include Aux)
|<-----------X--X--------X------>|  Accepted(N,I,V)
|            |  |        |       |  -- Reconfigure : Quorum = 2 --
X----------->|->|        |       |  Accept!(N,I+1,W) (Aux not participating)
|<-----------X--X--------------->|  Accepted(N,I+1,W)
|            |  |        |       |

Fast Paxos

Fast Paxos generalizes Basic Paxos to reduce end-to-end message delays. In Basic Paxos, the message delay from client request to learning is 3 message delays. Fast Paxos allows 2 message delays, but requires that (1) the system be composed of 3f+ 1 acceptors to tolerate up to f faults (instead of the classic 2f+1), and (2) the Client to send its request to multiple destinations.

Intuitively, if the leader has no value to propose, then a client could send an Accept! message to the Acceptors directly. The Acceptors would respond as in Basic Paxos, sending Accepted messages to the leader and every Learner achieving two message delays from Client to Learner.

If the leader detects a collision, it resolves the collision by sending Accept! messages for a new round which are Accepted as usual. This coordinated recovery technique requires four message delays from Client to Learner.

The final optimization occurs when the leader specifies a recovery technique in advance, allowing the Acceptors to perform the collision recovery themselves. Thus, uncoordinated collision recovery can occur in three message delays (and only two message delays if all Learners are also Acceptors).

Message flow: Fast Paxos, non-conflicting

Client    Leader         Acceptor      Learner
   |         |          |  |  |  |       |  |
   |         X--------->|->|->|->|       |  |  Any(N,I,Recovery)
   |         |          |  |  |  |       |  |
   X------------------->|->|->|->|       |  |  Accept!(N,I,W)
   |         |<---------X--X--X--X------>|->|  Accepted(N,I,W)
   |<------------------------------------X--X  Response(W)
   |         |          |  |  |  |       |  |

Message flow: Fast Paxos, conflicting proposals

Conflicting proposals with coordinated recovery. Note: the protocol does not specify how to handle the dropped client request.

Client   Leader      Acceptor     Learner
 |  |      |        |  |  |  |      |  |
 |  |      |        |  |  |  |      |  |
 |  |      |        |  |  |  |      |  |  !! Concurrent conflicting proposals
 |  |      |        |  |  |  |      |  |  !!   received in different order
 |  |      |        |  |  |  |      |  |  !!   by the Acceptors
 |  X--------------?|-?|-?|-?|      |  |  Accept!(N,I,V)
 X-----------------?|-?|-?|-?|      |  |  Accept!(N,I,W)
 |  |      |        |  |  |  |      |  |
 |  |      |        |  |  |  |      |  |  !! Acceptors disagree on value
 |  |      |<-------X--X->|->|----->|->|  Accepted(N,I,V)
 |  |      |<-------|<-|<-X--X----->|->|  Accepted(N,I,W)
 |  |      |        |  |  |  |      |  |
 |  |      |        |  |  |  |      |  |  !! Detect collision & recover
 |  |      X------->|->|->|->|      |  |  Accept!(N+1,I,W)
 |  |      |<-------X--X--X--X----->|->|  Accepted(N+1,I,W)
 |<---------------------------------X--X  Response(W)
 |  |      |        |  |  |  |      |  |

Conflicting proposals with uncoordinated recovery.

Client   Leader      Acceptor     Learner
 |  |      |        |  |  |  |      |  |
 |  |      X------->|->|->|->|      |  |  Any(N,I,Recovery)
 |  |      |        |  |  |  |      |  |
 |  |      |        |  |  |  |      |  |  !! Concurrent conflicting proposals
 |  |      |        |  |  |  |      |  |  !!   received in different order
 |  |      |        |  |  |  |      |  |  !!   by the Acceptors
 |  X--------------?|-?|-?|-?|      |  |  Accept!(N,I,V)
 X-----------------?|-?|-?|-?|      |  |  Accept!(N,I,W)
 |  |      |        |  |  |  |      |  |
 |  |      |        |  |  |  |      |  |  !! Acceptors disagree on value
 |  |      |<-------X--X->|->|----->|->|  Accepted(N,I,V)
 |  |      |<-------|<-|<-X--X----->|->|  Accepted(N,I,W)
 |  |      |        |  |  |  |      |  |
 |  |      |        |  |  |  |      |  |  !! Detect collision & recover
 |  |      |<-------X--X--X--X----->|->|  Accepted(N+1,I,W)
 |<---------------------------------X--X  Response(W)
 |  |      |        |  |  |  |      |  |

Message flow: Fast Paxos with uncoordinated recovery, collapsed roles

(merged Acceptor/Learner roles)

Client         Servers
 |  |         |  |  |  |
 |  |         X->|->|->|  Any(N,I,Recovery)
 |  |         |  |  |  |
 |  |         |  |  |  |  !! Concurrent conflicting proposals
 |  |         |  |  |  |  !!   received in different order
 |  |         |  |  |  |  !!   by the Servers
 |  X--------?|-?|-?|-?|  Accept!(N,I,V)
 X-----------?|-?|-?|-?|  Accept!(N,I,W)
 |  |         |  |  |  |
 |  |         |  |  |  |  !! Servers disagree on value
 |  |         X<>X->|->|  Accepted(N,I,V)
 |  |         |<-|<-X<>X  Accepted(N,I,W)
 |  |         |  |  |  |
 |  |         |  |  |  |  !! Detect collision & recover
 |  |         X<>X<>X<>X  Accepted(N+1,I,W)
 |<-----------X--X--X--X  Response(W)
 |  |         |  |  |  |

Generalized Paxos

Generalized consensus explores the relationship between the operations of the replicated state machine and the consensus protocol that implements it.^[16] The main discovery involves optimizations of Paxos when conflicting proposals could be applied in any order. i.e., when the proposed operations are commutative operations for the state machine. In such cases, the conflicting operations can both be accepted, avoiding the delays required for resolving conflicts and re-proposing the rejected operations.

This concept is further generalized into ever-growing sequences of commutative operations, some of which are known to be stable (and thus may be executed). The protocol tracks these sequences ensuring that all proposed operations of one sequence are stabilized before allowing any operation non-commuting with them to become stable.

Example

In order to illustrate Generalized Paxos, the example below shows a message flow between two concurrently executing clients and a replicated state machine implementing read/write operations over two distinct registers A and B.

Commutativity Table
	Read(A)	Write(A)	Read(B)	Write(B)
Read(A)
Write(A)
Read(B)
Write(B)

Note that in this table indicates operations which are non-commutative.

A possible sequence of operations :

 <1:Read(A), 2:Read(B), 3:Write(B), 4:Read(B), 5:Read(A), 6:Write(A)>

Since 5:Read(A) commutes with both 3:Write(B) and 4:Read(B), one possible permutation equivalent to the previous order is the following:

 <1:Read(A), 2:Read(B), 5:Read(A), 3:Write(B), 4:Read(B), 6:Write(A)>

In practice, a commute occurs only when operations are proposed concurrently.

Message flow: Generalized Paxos (example)

Responses not shown. Note: message abbreviations differ from previous message flows due to specifics of the protocol, see ^[23] for a full discussion.

Client      Leader  Acceptor       Learner
 |  |         |      |  |  |         |  |  !! New Leader Begins Round
 |  |         X----->|->|->|         |  |  Prepare(N)
 |  |         |<-----X- X- X         |  |  Promise(N,null)
 |  |         X----->|->|->|         |  |  Phase2Start(N,null)
 |  |         |      |  |  |         |  | 
 |  |         |      |  |  |         |  |  !! Concurrent commuting proposals
 |  X------- ?|-----?|-?|-?|         |  |  Propose(ReadA)
 X-----------?|-----?|-?|-?|         |  |  Propose(ReadB)
 |  |         X------X-------------->|->|  Accepted(N,<ReadA,ReadB>)
 |  |         |<--------X--X-------->|->|  Accepted(N,<ReadB,ReadA>)
 |  |         |      |  |  |         |  |
 |  |         |      |  |  |         |  |  !! No Conflict, both accepted
 |  |         |      |  |  |         |  |  Stable = <ReadA, ReadB>
 |  |         |      |  |  |         |  |
 |  |         |      |  |  |         |  |  !! Concurrent conflicting proposals
 X-----------?|-----?|-?|-?|         |  |  Propose(<WriteB,ReadA>)
 |  X--------?|-----?|-?|-?|         |  |  Propose(ReadB)
 |  |         |      |  |  |         |  |
 |  |         X------X-------------->|->|  Accepted(N,<WriteB,ReadA> . <ReadB>)
 |  |         |<--------X--X-------->|->|  Accepted(N,<ReadB> . <WriteB,ReadA>)
 |  |         |      |  |  |         |  |
 |  |         |      |  |  |         |  |  !! Conflict detected, leader chooses
 |  |         |      |  |  |         |  |  commutative order:
 |  |         |      |  |  |         |  |  V = <ReadA, WriteB, ReadB>
 |  |         |      |  |  |         |  |
 |  |         X----->|->|->|         |  |  Phase2Start(N+1,V)
 |  |         |<-----X- X- X-------->|->|  Accepted(N+1,V)
 |  |         |      |  |  |         |  |  Stable = <ReadA, ReadB> .
 |  |         |      |  |  |         |  |           <ReadA, WriteB, ReadB>
 |  |         |      |  |  |         |  |
 |  |         |      |  |  |         |  | !! More conflicting proposals
 X-----------?|-----?|-?|-?|         |  |  Propose(WriteA)
 |  X--------?|-----?|-?|-?|         |  |  Propose(ReadA)
 |  |         |      |  |  |         |  |
 |  |         X------X-------------->|->|  Accepted(N+1,<WriteA> . <ReadA>)
 |  |         |<--------X- X-------->|->|  Accepted(N+1,<ReadA> . <WriteA>)
 |  |         |      |  |  |         |  |
 |  |         |      |  |  |         |  |  !! Leader chooses order:
 |  |         |      |  |  |         |  |  W = <WriteA, ReadA>
 |  |         |      |  |  |         |  |
 |  |         X----->|->|->|         |  |  Phase2Start(N+2,W)
 |  |         |<-----X- X- X-------->|->|  Accepted(N+2,W)
 |  |         |      |  |  |         |  |  Stable = <ReadA, ReadB> .
 |  |         |      |  |  |         |  |           <ReadA, WriteB, ReadB> .
 |  |         |      |  |  |         |  |           <WriteA, ReadA>
 |  |         |      |  |  |         |  |

Performance

The above message flow shows us that Generalized Paxos can leverage operation semantics to avoid collisions when the spontaneous ordering of the network fails. This allows the protocol to be in practice quicker than Fast Paxos. However, when a collision occurs, Generalized Paxos needs two additional round trips to recover. This situation is illustrated with operations WriteB and ReadB in the above schema.

In the general case, such round trips are unavoidable and come from the fact that multiple commands can be accepted during a round. This makes the protocol more expensive than Paxos when conflicts are frequent. Hopefully two possible refinements of Generalized Paxos are possible to improve recovery time.^[24]

First, if the coordinator is part of every quorum of acceptors (round N is said centered), then to recover at round N+1 from a collision at round N, the coordinator skips phase 1 and proposes at phase 2 the sequence it accepted last during round N. This reduces the cost of recovery to a single round trip.
Second, if both rounds N and N+1 use a unique and identical centered quorum, when an acceptor detects a collision at round N, it spontaneously proposes at round N+1 a sequence suffixing both (i) the sequence accepted at round N by the coordinator and (ii) the greatest non-conflicting prefix it accepted at round N. For instance, if the coordinator and the acceptor accepted respectively at round N <WriteB, ReadB> and <ReadB, ReadA> , the acceptor will spontaneously accept <WriteB, ReadB, ReadA> at round N+1. With this variation, the cost of recovery is a single message delay which is obviously optimal. Notice here that the use of a unique quorum at a round does not harm liveness. This comes from the fact that any process in this quorum is a read quorum for the prepare phase of the next rounds.^[25]

Byzantine Paxos

Paxos may also be extended to support arbitrary failures of the participants, including lying, fabrication of messages, collusion with other participants, selective non-participation, etc. These types of failures are called Byzantine failures, after the solution popularized by Lamport.^[26]

Byzantine Paxos^[27] introduced by Castro and Liskov adds an extra message (Verify) which acts to distribute knowledge and verify the actions of the other processors:

Message flow: Byzantine Multi-Paxos, steady state

Client   Proposer      Acceptor     Learner
   |         |          |  |  |       |  |
   X-------->|          |  |  |       |  |  Request
   |         X--------->|->|->|       |  |  Accept!(N,I,V)
   |         |          X<>X<>X       |  |  Verify(N,I,V) - BROADCAST
   |         |<---------X--X--X------>|->|  Accepted(N,V)
   |<---------------------------------X--X  Response(V)
   |         |          |  |  |       |  |

Fast Byzantine Paxos^[28] introduced by Martin and Alvisi removes this extra delay, since the client sends commands directly to the Acceptors.

Note the Accepted message in Fast Byzantine Paxos is sent to all Acceptors and all Learners, while Fast Paxos sends Accepted messages only to Learners):

Message flow: Fast Byzantine Multi-Paxos, steady state

Client    Acceptor     Learner
   |      |  |  |       |  |
   X----->|->|->|       |  |  Accept!(N,I,V)
   |      X<>X<>X------>|->|  Accepted(N,I,V) - BROADCAST
   |<-------------------X--X  Response(V)
   |      |  |  |       |  |

The failure scenario is the same for both protocols; Each Learner waits to receive F+1 identical messages from different Acceptors. If this does not occur, the Acceptors themselves will also be aware of it (since they exchanged each other's messages in the broadcast round), and correct Acceptors will re-broadcast the agreed value:

Message flow: Fast Byzantine Multi-Paxos, failure

Client    Acceptor     Learner
   |      |  |  !       |  |  !! One Acceptor is faulty
   X----->|->|->!       |  |  Accept!(N,I,V)
   |      X<>X<>X------>|->|  Accepted(N,I,{V,W}) - BROADCAST
   |      |  |  !       |  |  !! Learners receive 2 different commands
   |      |  |  !       |  |  !! Correct Acceptors notice error and choose
   |      X<>X<>X------>|->|  Accepted(N,I,V) - BROADCAST
   |<-------------------X--X  Response(V)
   |      |  |  !       |  |

Adapting Paxos for RDMA networks

With the emergence of very high speed reliable datacenter networks that support remote DMA (RDMA), there has been substantial interest in optimizing Paxos to leverage hardware offloading, in which the network interface card and network routers provide reliability and network-layer congestion control, freeing the host CPU for other tasks. The Derecho C++ Paxos library is an open-source Paxos implementation that explores this option.^[12]

Derecho offers both a classic Paxos, with data durability across full shutdown/restart sequences, and vertical Paxos (atomic multicast), for in-memory replication and state-machine synchronization. The Paxos protocols employed by Derecho needed to be adapted to maximize asynchronous data streaming and remove other sources of delay on the leader's critical path. So doing enables Derecho to sustain the full bidirectional RDMA data rate. In contrast, although traditional Paxos protocols can be migrated to an RDMA network by simply mapping the message send operations to native RDMA operations, doing so leaves round-trip delays on the critical path. In high-speed RDMA networks, even small delays can be large enough to prevent utilization of the full potential bandwidth.

Production use of Paxos

Google uses the Paxos algorithm in their Chubby distributed lock service in order to keep replicas consistent in case of failure.^[29] Chubby is used by Bigtable which is now in production in Google Analytics and other products.
Google Spanner and Megastore use the Paxos algorithm internally.
The OpenReplica replication service uses Paxos to maintain replicas for an open access system that enables users to create fault-tolerant objects. It provides high performance through concurrent rounds and flexibility through dynamic membership changes.
IBM supposedly uses the Paxos algorithm in their IBM SAN Volume Controller product to implement a general purpose fault-tolerant virtual machine used to run the configuration and control components of the storage virtualization services offered by the cluster. (Original MIT & IBM research paper)
Microsoft uses Paxos in the Autopilot cluster management service from Bing, and in Windows Server Failover Clustering.
WANdisco have implemented Paxos within their DConE active-active replication technology.^[30]
XtreemFS uses a Paxos-based lease negotiation algorithm for fault-tolerant and consistent replication of file data and metadata.^[31]
Heroku uses Doozerd which implements Paxos for its consistent distributed data store.
Ceph uses Paxos as part of the monitor processes to agree which OSDs are up and in the cluster.
The MariaDB Xpand distributed SQL database uses Paxos for distributed transaction resolution.
Neo4j HA graph database implements Paxos, replacing Apache ZooKeeper from v1.9
Apache Cassandra NoSQL database uses Paxos for Light Weight Transaction feature only
Amazon Elastic Container Services uses Paxos to maintain a consistent view of cluster state
Amazon DynamoDB uses the Paxos algorithm for leader election and consensus.

References

↑ Pease, Marshall; Shostak, Robert; Lamport, Leslie (April 1980). "Reaching Agreement in the Presence of Faults". Journal of the Association for Computing Machinery 27 (2): 228–234. doi:10.1145/322186.322188. http://research.microsoft.com/users/lamport/pubs/pubs.html#reaching. Retrieved 2007-02-02.
↑ Lamport, Leslie (July 1978). "Time, Clocks and the Ordering of Events in a Distributed System". Communications of the ACM 21 (7): 558–565. doi:10.1145/359545.359563. http://research.microsoft.com/users/lamport/pubs/pubs.html#time-clocks. Retrieved 2007-02-02.
↑ Schneider, Fred (1990). "Implementing Fault-Tolerant Services Using the State Machine Approach: A Tutorial". ACM Computing Surveys 22 (4): 299–319. doi:10.1145/98163.98167. http://www.cs.cornell.edu/fbs/publications/smsurvey.pdf.
↑ Leslie Lamport's history of the paper
↑ Lamport, Leslie (May 1998). "The Part-Time Parliament". ACM Transactions on Computer Systems 16 (2): 133–169. doi:10.1145/279227.279229. http://research.microsoft.com/users/lamport/pubs/pubs.html#lamport-paxos. Retrieved 2007-02-02.
↑ ^6.0 ^6.1 Fischer, M. (April 1985). "Impossibility of distributed consensus with one faulty process". Journal of the ACM 32 (2): 374–382. doi:10.1145/3149.214121.
↑ Dwork, Cynthia; Lynch, Nancy; Stockmeyer, Larry (April 1988). "Consensus in the Presence of Partial Synchrony". Journal of the ACM 35 (2): 288–323. doi:10.1145/42282.42283. http://groups.csail.mit.edu/tds/papers/Lynch/jacm88.pdf.
↑ Oki, Brian; Liskov, Barbara (1988). "Viewstamped Replication: A New Primary Copy Method to Support Highly-Available Distributed Systems". pp. 8–17. doi:10.1145/62546.62549. http://portal.acm.org/citation.cfm?id=62549.
↑ Birman, Kenneth; Joseph, Thomas (February 1987). "Reliable Communication in the Presence of Failures". ACM Transactions on Computer Systems 5: 47–76. doi:10.1145/7351.7478.
↑ Lamport, Leslie; Malkhi, Dahlia; Zhou, Lidong (March 2010). "Reconfiguring a State Machine". SIGACT News 41 (1): 63–73. doi:10.1145/1753171.1753191.
↑ Keidar; Shraer, Alexander (2006). "Timeliness, failure-detectors, and consensus performance.". doi:10.1145/1146381.1146408.
↑ ^12.0 ^12.1 Jha, Sagar; Behrens, Jonathan; Gkountouvas, Theo; Milano, Matthew; Song, Weijia; Tremel, Edward; van Renesse, Robbert; Zink, Sydney et al. (April 2019). "Derecho: Fast State Machine Replication for Cloud Services". ACM Transactions on Computer Systems 36 (2). doi:10.1145/3302258.
↑ Lamport, Leslie (2004). "Lower Bounds for Asynchronous Consensus". http://research.microsoft.com/users/lamport/pubs/pubs.html#lower-bound.
↑ Van Renesse, Robbert; Altinbuken, Deniz (2015-02-17). "Paxos Made Moderately Complex". ACM Computing Surveys 47 (3): 42:1–42:36. doi:10.1145/2673577. ISSN 0360-0300. https://doi.org/10.1145/2673577.
↑ ^15.0 ^15.1 ^15.2 ^15.3 ^15.4 Lamport, Leslie (2005). "Fast Paxos". http://research.microsoft.com/users/lamport/pubs/pubs.html#fast-paxos.
↑ ^16.0 ^16.1 ^16.2 ^16.3 Lamport, Leslie (2005). Generalized Consensus and Paxos. http://research.microsoft.com/users/lamport/pubs/pubs.html#generalized.
↑ Chandra, Tushar; Griesemer, Robert; Redstone, Joshua (2007). "Paxos made live". Proceedings of the twenty-sixth annual ACM symposium on Principles of distributed computing. pp. 398–407. doi:10.1145/1281100.1281103. ISBN 9781595936165. http://research.google.com/pubs/pub33002.html.
↑ Quesada Torres, Luis (2018). The Paxos Algorithm. Google TechTalks.
↑ Lamport, Leslie (2001). Paxos Made Simple ACM SIGACT News (Distributed Computing Column) 32, 4 (Whole Number 121, December 2001) 51-58.
↑ "Leader Election, Why Should I Care?". Elastic Blog. 13 September 2013. https://www.elastic.co/blog/found-leader-election-in-general.
↑ I. Gupta, R. van Renesse, and K. P. Birman, 2000, A Probabilistically Correct Leader Election Protocol for Large Groups, Technical Report , Cornell University
↑ ^22.0 ^22.1 ^22.2 ^22.3 ^22.4 Lamport, Leslie; Massa, Mike (2004). "Cheap Paxos". http://research.microsoft.com/users/lamport/pubs/pubs.html#web-dsn-submission.
↑ Turner, Bryan (2007). "The Paxos Family of Consensus Protocols". http://www.fractalscape.org/2007/10/01/paxos-family.html.
↑ Pierre, Sutra; Marc, Shapiro (2011). "Fast Genuine Generalized Consensus". http://pagesperso-systeme.lip6.fr/Marc.Shapiro/papers/FGGC-SRDS-2011.pdf.
↑ Lamport, Leslie; Malkhi, Dahlia; Zhou, Lidong (2009). "Vertical paxos and primary-backup replication". Proceedings of the 28th ACM symposium on Principles of distributed computing. PODC '09. New York, NY, USA: ACM. pp. 312–313. doi:10.1145/1582716.1582783. ISBN 9781605583969.
↑ Lamport, Leslie; Shostak, Robert; Pease, Marshall (July 1982). "The Byzantine Generals Problem". ACM Transactions on Programming Languages and Systems 4 (3): 382–401. doi:10.1145/357172.357176. http://research.microsoft.com/users/lamport/pubs/pubs.html#byz. Retrieved 2007-02-02.
↑ Castro, Miguel; Liskov, Barbara (February 1999). "Practical Byzantine Fault Tolerance". Proceedings of the Third Symposium on Operating Systems Design and Implementation: 173–186. http://pmg.csail.mit.edu/papers/osdi99.pdf. Retrieved 5 March 2018.
↑ Martin, Jean-Philippe; Alvisi, Lorenzo (July 2006). "Fast Byzantine Consensus". IEEE Transactions on Dependable and Secure Computing 3 (3): 202–215. doi:10.1109/TDSC.2006.35. https://www.cs.utexas.edu/~lorenzo/papers/fab.pdf. Retrieved 5 March 2018.
↑ Burrows, Mike. "The Chubby lock service for loosely-coupled distributed systems". OSDI. https://static.googleusercontent.com/media/research.google.com/en//archive/chubby-osdi06.pdf.
↑ Aahlad et al.(2011). “The Distributed Coordination Engine (DConE)” . WANdisco white paper.
↑ Kolbeck, Björn; Högqvist, Mikael; Stender, Jan; Hupfeld, Felix (2011). “Flease - Lease Coordination without a Lock Server”. 25th IEEE International Parallel & Distributed Processing Symposium (IPDPS 2011).

External links

0.00

(0 votes)

Original source: https://en.wikipedia.org/wiki/Paxos (computer science). Read more

[agree-1] Pease, Marshall; Shostak, Robert; Lamport, Leslie (April 1980). "Reaching Agreement in the Presence of Faults". Journal of the Association for Computing Machinery 27 (2): 228–234. doi:10.1145/322186.322188. http://research.microsoft.com/users/lamport/pubs/pubs.html#reaching. Retrieved 2007-02-02.

[clocks-2] Lamport, Leslie (July 1978). "Time, Clocks and the Ordering of Events in a Distributed System". Communications of the ACM 21 (7): 558–565. doi:10.1145/359545.359563. http://research.microsoft.com/users/lamport/pubs/pubs.html#time-clocks. Retrieved 2007-02-02.

[schneider-3] Schneider, Fred (1990). "Implementing Fault-Tolerant Services Using the State Machine Approach: A Tutorial". ACM Computing Surveys 22 (4): 299–319. doi:10.1145/98163.98167. http://www.cs.cornell.edu/fbs/publications/smsurvey.pdf.

[Lamport-4] Leslie Lamport's history of the paper

[paxos-5] Lamport, Leslie (May 1998). "The Part-Time Parliament". ACM Transactions on Computer Systems 16 (2): 133–169. doi:10.1145/279227.279229. http://research.microsoft.com/users/lamport/pubs/pubs.html#lamport-paxos. Retrieved 2007-02-02.

[flp-6] 6.0 ^6.1 Fischer, M. (April 1985). "Impossibility of distributed consensus with one faulty process". Journal of the ACM 32 (2): 374–382. doi:10.1145/3149.214121.

[LDS88-7] Dwork, Cynthia; Lynch, Nancy; Stockmeyer, Larry (April 1988). "Consensus in the Presence of Partial Synchrony". Journal of the ACM 35 (2): 288–323. doi:10.1145/42282.42283. http://groups.csail.mit.edu/tds/papers/Lynch/jacm88.pdf.

[vr-8] Oki, Brian; Liskov, Barbara (1988). "Viewstamped Replication: A New Primary Copy Method to Support Highly-Available Distributed Systems". pp. 8–17. doi:10.1145/62546.62549. http://portal.acm.org/citation.cfm?id=62549.

[BJ87-9] Birman, Kenneth; Joseph, Thomas (February 1987). "Reliable Communication in the Presence of Failures". ACM Transactions on Computer Systems 5: 47–76. doi:10.1145/7351.7478.

[LMZ10-10] Lamport, Leslie; Malkhi, Dahlia; Zhou, Lidong (March 2010). "Reconfiguring a State Machine". SIGACT News 41 (1): 63–73. doi:10.1145/1753171.1753191.

[optimality-11] Keidar; Shraer, Alexander (2006). "Timeliness, failure-detectors, and consensus performance.". doi:10.1145/1146381.1146408.

[Derecho-12] 12.0 ^12.1 Jha, Sagar; Behrens, Jonathan; Gkountouvas, Theo; Milano, Matthew; Song, Weijia; Tremel, Edward; van Renesse, Robbert; Zink, Sydney et al. (April 2019). "Derecho: Fast State Machine Replication for Cloud Services". ACM Transactions on Computer Systems 36 (2). doi:10.1145/3302258.

[consensus-13] Lamport, Leslie (2004). "Lower Bounds for Asynchronous Consensus". http://research.microsoft.com/users/lamport/pubs/pubs.html#lower-bound.

[14] Van Renesse, Robbert; Altinbuken, Deniz (2015-02-17). "Paxos Made Moderately Complex". ACM Computing Surveys 47 (3): 42:1–42:36. doi:10.1145/2673577. ISSN 0360-0300. https://doi.org/10.1145/2673577.

[fast-15] 15.0 ^15.1 ^15.2 ^15.3 ^15.4 Lamport, Leslie (2005). "Fast Paxos". http://research.microsoft.com/users/lamport/pubs/pubs.html#fast-paxos.

[general-16] 16.0 ^16.1 ^16.2 ^16.3 Lamport, Leslie (2005). Generalized Consensus and Paxos. http://research.microsoft.com/users/lamport/pubs/pubs.html#generalized.

[live-17] Chandra, Tushar; Griesemer, Robert; Redstone, Joshua (2007). "Paxos made live". Proceedings of the twenty-sixth annual ACM symposium on Principles of distributed computing. pp. 398–407. doi:10.1145/1281100.1281103. ISBN 9781595936165. http://research.google.com/pubs/pub33002.html.

[techtalk-18] Quesada Torres, Luis (2018). The Paxos Algorithm. Google TechTalks.

[paxos-simple-19] Lamport, Leslie (2001). Paxos Made Simple ACM SIGACT News (Distributed Computing Column) 32, 4 (Whole Number 121, December 2001) 51-58.

[elas_Lead-20] "Leader Election, Why Should I Care?". Elastic Blog. 13 September 2013. https://www.elastic.co/blog/found-leader-election-in-general.

[21] I. Gupta, R. van Renesse, and K. P. Birman, 2000, A Probabilistically Correct Leader Election Protocol for Large Groups, Technical Report , Cornell University

[cheap-22] 22.0 ^22.1 ^22.2 ^22.3 ^22.4 Lamport, Leslie; Massa, Mike (2004). "Cheap Paxos". http://research.microsoft.com/users/lamport/pubs/pubs.html#web-dsn-submission.

[paxos-family-23] Turner, Bryan (2007). "The Paxos Family of Consensus Protocols". http://www.fractalscape.org/2007/10/01/paxos-family.html.

[fggc-24] Pierre, Sutra; Marc, Shapiro (2011). "Fast Genuine Generalized Consensus". http://pagesperso-systeme.lip6.fr/Marc.Shapiro/papers/FGGC-SRDS-2011.pdf.

[25] Lamport, Leslie; Malkhi, Dahlia; Zhou, Lidong (2009). "Vertical paxos and primary-backup replication". Proceedings of the 28th ACM symposium on Principles of distributed computing. PODC '09. New York, NY, USA: ACM. pp. 312–313. doi:10.1145/1582716.1582783. ISBN 9781605583969.

[byzgen-26] Lamport, Leslie; Shostak, Robert; Pease, Marshall (July 1982). "The Byzantine Generals Problem". ACM Transactions on Programming Languages and Systems 4 (3): 382–401. doi:10.1145/357172.357176. http://research.microsoft.com/users/lamport/pubs/pubs.html#byz. Retrieved 2007-02-02.

[27] Castro, Miguel; Liskov, Barbara (February 1999). "Practical Byzantine Fault Tolerance". Proceedings of the Third Symposium on Operating Systems Design and Implementation: 173–186. http://pmg.csail.mit.edu/papers/osdi99.pdf. Retrieved 5 March 2018.

[28] Martin, Jean-Philippe; Alvisi, Lorenzo (July 2006). "Fast Byzantine Consensus". IEEE Transactions on Dependable and Secure Computing 3 (3): 202–215. doi:10.1109/TDSC.2006.35. https://www.cs.utexas.edu/~lorenzo/papers/fab.pdf. Retrieved 5 March 2018.

[29] Burrows, Mike. "The Chubby lock service for loosely-coupled distributed systems". OSDI. https://static.googleusercontent.com/media/research.google.com/en//archive/chubby-osdi06.pdf.

[WANdisco-30] Aahlad et al.(2011). “The Distributed Coordination Engine (DConE)” . WANdisco white paper.

[flease-31] Kolbeck, Björn; Högqvist, Mikael; Stender, Jan; Hupfeld, Felix (2011). “Flease - Lease Coordination without a Lock Server”. 25th IEEE International Parallel & Distributed Processing Symposium (IPDPS 2011).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]