Plausible reasoning
Topic: Philosophy
 From HandWiki - Reading time: 8 min
From HandWiki - Reading time: 8 min
Plausible reasoning is a method of deriving new conclusions from given known premises, a method different from the classical syllogistic argumentation methods of Aristotelian two-valued logic. The syllogistic style of argumentation is illustrated by the oft-quoted argument "All men are mortal, Socrates is a man, and therefore, Socrates is mortal." In contrast, consider the statement "if it is raining then it is cloudy." The only logical inference that one can draw from this is that "if it is not cloudy then it is not raining." But ordinary people in their everyday lives would conclude that "if it is not raining then being cloudy is less plausible," or "if it is cloudy then rain is more plausible." The unstated and unconsciously applied reasoning, arguably incorrect, that made people come to their conclusions is typical of plausible reasoning .
As another example,[1] "Suppose some dark night a policeman walks down a street, apparently deserted; but suddenly he hears a burglar alarm, looks across the street, and sees a jewellery store with a broken window. Then a person wearing a mask comes crawling out through the broken window, carrying a bag which turns out to be full of expensive jewellery. The policeman immediately concludes that this person is stealing the jewellery." The question is the reasoning process by which the policeman arrives at this conclusion.
The policeman's conclusion was not a logical deduction from the evidence. There may be a perfectly valid explanation for everything. For example, it might be that this person was the owner of the jewellery store and he was coming home from a fancy dress competition, and he didn't have the key with him. But just as he walked by his store a passing truck threw a stone through the window; and he was only protecting his own property and not stealing the jewellery. Now whatever be the policeman's reasoning process, it has a certain degree of validity. The evidence did not prove that the person was stealing jewellery, but it did make it extremely plausible. This is an example of a kind of reasoning, often referred to as plausible reasoning, in which most people are generally very proficient.
Plausibility reasoning in ancient Greece
During the fifth century B.C.E.,[2] judicial orators in Greek Sicily developed a method for successfully pleading their cases in such instances in which no eyewitnesses or written documents or other such direct evidence could be produced. They began to base their arguments on the internal or external probability or plausibility of their statements. This new way of arguing was commonly labeled with the Greek term eikós, a term that has been variously rendered as similarity, likelihood, probability or plausibility. The success of the argument depends on the oratorical skills of the speaker, arguments by eikós have often been accused of lack of truthfulness. Here is a classical example of argument by plausible reasoning presented by Aristotle in his Rhetoric:
"If the accused is not open to the charge – for instance if a weakling be tried for violent assault – the defence is that he was not likely (eikós) to do such a thing. But if he is open to the charge – that is, if he is a strong man – the defence is still that he was not likely (eikós) to do such a thing, since he could be sure that people would think he was likely (eikós) to do it."
The sophists, a sort of mendicant academicians were said to have been experts in this type of argumentation and they are said to have taught wealthy young Greeks these methods for a hefty fee. Plato and Aristotle strongly denounced these methods and the method came to acquire a lot of bad repute. Sophistic argumentation styles were equated with fallacious arguments.
George Polya and plausible reasoning
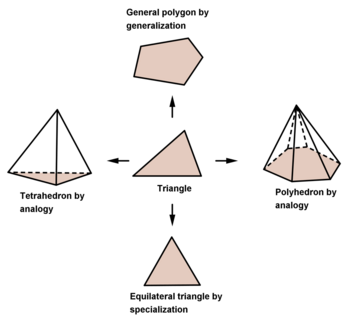
George Polya in his two volume book titled Mathematics and Plausible Reasoning[3][4] presents plausible reasoning as a way of generating new mathematical conjectures. To Polya, “a mathematical proof is demonstrative reasoning but the inductive evidence of the physicist, the circumstantial evidence of the lawyer, the documentary evidence of the historian and the statistical evidence of the economist all belong to plausible reasoning”. Polya’s intention is to teach students the art of guessing new results in mathematics for which he marshals such notions as induction and analogy as possible sources for plausible reasoning. The first volume of the book is devoted to an extensive discussion of these ideas with several examples drawn from various field of mathematics.
In the Preface to Volume 1 of the book Polya exhorts all interested students of mathematics thus: "Certainly, let us learn proving, but also let us learn guessing." P. R. Halmos reviewing the book summarized the central thesis of the book thus: ". . . a good guess is as important as a good proof."[5]
Volume I: Induction and analogy in mathematics
Polya begins Volume I with a discussion on inductive reasoning (not mathematical induction) as a way of guessing new results. He shows how the chance observations of a few results of the form 4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5, 10 = 3 + 7, etc., may prompt a sharp mind to formulate the conjecture that every even number greater than 4 can be represented as the sum of two odd prime numbers. This is the well known Goldbach's conjecture. The first problem in the first chapter is to guess the rule according to which the successive terms of the following sequence are chosen: 11, 31, 41, 61, 71, 101, 131, . . . In the next chapter the techniques of generalization, specialization and analogy are presented as possible strategies for plausible reasoning. In the remaining chapters, these ideas are illustrated by discussing the discovery of several results in various fields of mathematics like number theory, geometry, etc. and also in physical sciences.
Volume II: Patterns of Plausible Inference
This volume attempts to formulate certain patterns of plausible reasoning. The relations of these patterns with the calculus of probability are also investigated. Their relation to mathematical invention and instruction are also discussed. The following are some of the patterns of plausible inference discussed by Polya.
| Sl. No. | Premise 1 | Premise 2 | Premise 3 | Plausible conclusion |
|---|---|---|---|---|
| 1 | A implies B | B true | - | A more credible |
| 2 | A implies Bn+1 | Bn+1 very different from the formerly verified consequences B1, B2, . . ., Bn of A | Bn+1 true | A much more credible |
| 3 | A implies Bn+1 | Bn+1 very similar to the formerly verified consequences B1, B2, . . ., Bn of A | Bn+1 true | A just a little more credible |
| 4 | A implies B | B very improbable in itself | B true | A very much more credible |
| 5 | A implies B | B quite probable in itself | B true | A just a little more credible |
| 6 | A analogous to B | B true | - | A more credible |
| 7 | A analogous to B | B more credible | -- | A somewhat more credible |
| 8 | A is implied by B | B false | -- | A less credible |
| 9 | A is incompatible with B | B false | -- | A more credible |
Characteristics of plausible argument
After a detailed analysis of several paradigmatic examples drawn from ancient Greek texts, D Walton and others formulated the following eleven properties as the defining characteristics of plausible reasoning.[6]
- Plausible reasoning proceeds from premises that are more plausible to a conclusion that was less plausible before the plausible argument.
- Something is found plausible when hearers have examples in their own minds.
- Plausible reasoning is based on common knowledge.
- Plausible reasoning is defeasible.
- Plausible reasoning is based on the way things generally go in familiar situations.
- Plausible reasoning can be used to fill in implicit premises in incomplete arguments.
- Plausible reasoning is commonly based on appearances from perception.
- Stability is an important characteristic of plausible reasoning.
- Plausible reasoning can be tested, and by this means, confirmed or refuted.
- Probing into plausible reasoning in a dialogue is a way of testing it.
- Plausible reasoning admits of degrees by testing, but of a kind different from those the standard probability values and Bayesian rules used in Pascalian probability
Some of the problems associated with the formulation of a theory of plausible reasoning
Allan M. Collins, a recognized authority on intelligent tutoring systems and plausible reasoning, presenting a core theory of the logic of plausible reasoning identified some of the important problems in the formulation of such a theory.[7]
1. Representing degree of belief.
This is the problem of representing the differences in the strengths of beliefs indicated by the phrases “entirely certain” and “would guess”.
2. Evaluating the strength of arguments.
We need a computational scheme to calculate and compare different levels and strengths of belief.
3. Applying rules of general but not universal validity.
Standard logic justifies the use of universally quantified rules; rules that are always true without exception. Much commonsense inference relies on applying default rules that hold in general but not always.
4. Avoiding the enumeration of all the conditions on a rule.
It often happens that a plausible commonsense rule, when examined closely, has an almost unlimited number of possible types of exceptions. The problem of dealing with all these potential exceptions is known as the qualification problem.
5. Inference from the absence of information.
It is often reasonable to infer that a statement A is false from the fact that one does not know A to be true, or from the fact that it is not stated to be true in a problem statement.
6. Limiting the extent of inference.
Many intuitively appealing sets of axioms have the property that the first few inferences all seem to be reasonable and to have reasonable conclusions, but that, as the inferences get further and further from the starting axioms, the conclusions seem less and less sensible, and they eventually end up in pure nonsense.
7. Inference using vague concepts.
Inferences that involve reasoning near the boundaries of a vague concept are often uncertain.
8. Finding expected utility.
This is the problem of choosing between actions whose consequences are uncertain. In such a case, a choice may be made based on the likelihoods of the various outcomes with their desirability.
9. Inferring an explanation.
Commonsense reasoners try to explain the reasons underlying their observations. If I observe that the street is wet, I infer that it rained. If I observe that the sidewalk is not wet, I may decide instead that the street-cleaners have been by.
10. Schema-Based Inference.
Many useful commonsense concepts correspond to large systems of relations that are instantiated in many separate instances in the world. Such concepts are called schemas or frames.
11. Inferring a general rule from examples.
People are always on the lookout for general rules that encapsulate their observations.
References
- ↑ E.T. Jaynes (2003). Probability Theory: The Logic of Science. Cambridge University Press. p. 3.
- ↑ Manfred Kraus. "Early Greek Probability Arguments and Common Ground in Dissensus". in H. V. Hansen. Dissensus and the Search for Common Ground. Windsor, ON: OSSA. pp. 1–11. http://scholar.uwindsor.ca/cgi/viewcontent.cgi?article=1344&context=ossaarchive. Retrieved 21 February 2015.
- ↑ George Polya (1954). Mathematics and Plausible Reasoning Volume I: Induction and Analogy in Mathematics. Princeton University Press.
- ↑ George Polya (1954). Mathematics and Plausible reasoning Volume II: Patterns of Plausible Inference. Princeton University Press.
- ↑ P. R. Halmos (1955). "Review: G. Polya, Mathematics and plausible reasoning". Bulletin of the American Mathematical Society 61 (3): 243–245. doi:10.1090/s0002-9904-1955-09904-x. http://projecteuclid.org/euclid.bams/1183519731. Retrieved 21 February 2015.
- ↑ D. Walton; C. W. Tindale; T. F. Gordon (2014). "Applying recent argumentation methods to some ancient examples of plausible reasoning". Argumentation 28 (1): 85–119. doi:10.1007/s10503-013-9306-y. Archived from the original on 21 February 2015. https://web.archive.org/web/20150221182745/http://www.dougwalton.ca/papers%20in%20pdf/14Ancient.pdf. Retrieved 21 February 2015.
- ↑ Allan Collins (1989). "The Logic of Plausible Reasoning: A Core Theory". Cognitive Science 13: 1–49. doi:10.1207/s15516709cog1301_1.
Further reading
- Glenn Shafer, Judea Pearl (Editors) (1990). Readings in Uncertain Reasoning. Morgan Kaufmann. ISBN 9781558601253. https://archive.org/details/readingsinuncert00shaf.
- Jonathan M. Borwein, David H. Bailey (2004). Mathematics by Experiment: Plausible Reasoning in 21st Century. A.K. Peters. ISBN 9781568812113.
- Judea Pearl (1988). Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. Morgan Kaufmann. ISBN 9781558604797. https://archive.org/details/probabilisticrea00pear.
 |
 KSF
KSF