Band offset

Band offset describes the relative alignment of the energy bands at a semiconductor heterojunction.

Introduction

At semiconductor heterojunctions, energy bands of two different materials come together, leading to an interaction. Both band structures are positioned discontinuously from each other, causing them to align close to the interface. This is done to ensure that the Fermi energy level stays continuous throughout the two semiconductors. This alignment is caused by the discontinuous band structures of the semiconductors when compared to each other and the interaction of the two surfaces at the interface. This relative alignment of the energy bands at such semiconductor heterojunctions is called the Band offset.

The band offsets can be determined by both intrinsic properties, that is, determined by properties of the bulk materials, as well as non-intrinsic properties, namely, specific properties of the interface. Depending on the type of the interface, the offsets can be very accurately considered intrinsic, or be able to be modified by manipulating the interfacial structure.^[1] Isovalent heterojunctions are generally insensitive to manipulation of the interfacial structure, whilst heterovalent heterojunctions can be influenced in their band offsets by the geometry, the orientation, and the bonds of the interface and the charge transfer between the heterovalent bonds.^[2] The band offsets, especially those at heterovalent heterojunctions depend significantly on the distribution of interface charge.

The band offsets are determined by two kinds of factors for the interface, the band discontinuities and the built-in potential. These discontinuities are caused by the difference in band gaps of the semiconductors and are distributed between two band discontinuities, the valence-band discontinuity, and the conduction-band discontinuity. The built-in potential is caused by the bands which bend close at the interface due to a charge imbalance between the two semiconductors, and can be described by Poisson's equation.

Semiconductor types

Here is showcased the different types of heterojunctions in semiconductors. In type I, the conduction band of the second semiconductor is lower than that of the first, whilst its valence band is higher than that of the first. As a consequence the band gap of the first semiconductor is larger than the band gap of the second semiconductor. In type II the conduction band and valence band of the second semiconductor are both lower than the bands of the first semiconductor. In this staggered gap, the band gap of the second semiconductor is no longer restricted to being smaller than the first semiconductor, although the band gap of the second semiconductor is still partially contained in the first semiconductor. In type III however, the conduction band of the second semiconductor overlaps with the valence band of the first semiconductor. Due to this overlap, there are no forbidden energies at the interface, and the band gap of the second semiconductor is no longer contained by the band gap of the first.

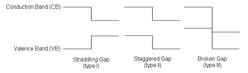
The behaviour of semiconductor heterojunctions depend on the alignment of the energy bands at the interface and thus on the band offsets. The interfaces of such heterojunctions can be categorized in three types: straddling gap (referred to as type I), staggered gap (type II), and broken gap (type III).

These representations do not take into account the band bending, which is a reasonable assumption if you only look at the interface itself, as band bending exerts its influence on a length scale of generally hundreds of angström. For a more accurate picture of the situation at hand, the inclusion of band bending is important.

In this heterojunction of type I alignment, one can clearly see the built-in potential Φbi = Φ(A) + Φ(B). The band gap difference ΔEg = Eg(A) - Eg(B) is distributed between the two discontinuities,ΔEv, and ΔEc$. In alignments, it is generally the case that the conduction band which has the higher energy minimum will bend upward, whilst the valence band which has the lower energy maximum will bend upward. In this type of alignment, this means that both of the bands of semiconductor A will bend upwards, whilst both of the bands of semiconductor B will bend downwards. The band bending, caused by the built-in potential, is determined by the interface position of the Fermi level, and predicting or measuring this level is related to the Schottky barrier height in metal-semiconductor interfaces. Depending on the doping of the bulk material, the band bending can be into the thousands of angstroms, or just fifty, depending on the doping. The discontinuities on the other hand, are primarily due to the electrostatic potential gradients of the abrupt interface, working on a length scale of ideally a single atomic interplanar spacing, and is almost independent of any doping used.

Experimental methods

Two kinds of experimental techniques are used to describe band offsets. The first is an older technique, the first technique to probe the heterojunction built-in potential and band discontinuities. This methods are generally called transport methods. These methods consist of two classes, either capacitance-voltage (C-V) or current-voltage (I-V) techniques. These older techniques were used to extract the built-in potential by assuming a square-root dependence for the capacitance C on [math]\displaystyle{ \Phi }[/math]_bi - qV, with [math]\displaystyle{ \Phi }[/math]_bi the built-in potential, q the electron charge, and V the applied voltage. If band extrema away from the interface, as well as the distance between the Fermi level, are known parameters, known a priori from bulk doping, it becomes possible to obtain the conduction band offset and the valence band offset. This square root dependence corresponds to an ideally abrupt transition at the interface and it may or may not be a good approximation of the real junction behaviour.^[1]

The second kind of technique consists of optical methods. Photon absorption is used effectively as the conduction band and valence band discontinuities define quantum wells for the electrons and the holes. Optical techniques can be used to probe the direct transitions between sub-bands within the quantum wells, and with a few parameters known, such as the geometry of the structure and the effective mass, the transition energy measured experimentally can be used to probe the well depth. Band offset values are usually estimated using the optical response as a function of certain geometrical parameters or the intensity of an applied magnetic field. Light scattering could also be used to determine the size of the well depth.

Alignment

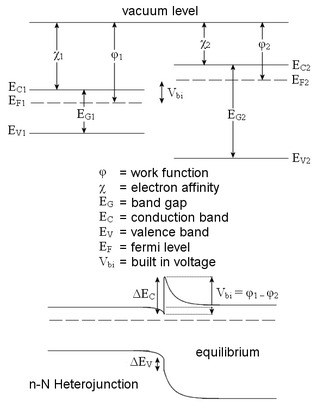
Prediction of the band alignment is at face value dependent on the heterojunction type, as well as whether or not the heterojunction in question is heterovalent or isovalent. However, quantifying this alignment proved a difficult task for a long time. Anderson's rule is used to construct energy band diagrams at heterojunctions between two semiconductors. It states that during the construction of an energy band diagram, the vacuum levels of the semiconductors on either side of the heterojunction should be equal.^[1]

Anderson's rule states that when we construct the heterojunction, we need to have both semiconductors on an equal vacuum energy level. This ensures that the energy bands of both the semiconductors are being held to the same reference point, from which ΔE_c and ΔE_v, the conduction band offset and valence band offset can be calculated. By having the same reference point for both semiconductors, ΔE_c becomes equal to the built-in potential, V_bi = Φ₁ - Φ₂, and the behaviour of the bands at the interface can be predicted as can be seen at the picture above.

Anderson's rule fails to predict real band offsets. This is primarily due to the fact that Anderson's model implies that the materials are assumed to behave the same as if they were separated by a large vacuum distance, however at these heterojunctions consisting of solids filling the space, there is no vacuum, and the use of the electron affinities at vacuum leads to wrong results. Anderson's rule ignores actual chemical bonding effects that occur on small vacuum separation or non-existent vacuum separation, which leads to wrong predictions about the band offsets.

A better theory for predicting band offsets has been linear-response theory. In this theory, interface dipoles have a significant impact on the lining up of the bands of the semiconductors. These interface dipoles however are not ions, rather they are mathematical constructs based upon the difference of charge density between the bulk and the interface. Linear-response theory is based on first-principles calculations, which are calculations aimed at solving the quantum-mechanical equations, without input from experiment. In this theory, the band offset is the sum of two terms, the first term is intrinsic and depends solely on the bulk properties, the second term, which vanishes for isovalent and abrupt non-polar heterojunctions, depends on the interface geometry, and can easily be calculated once the geometry is known, as well as certain quantities (such as the lattice parameters).

The goal of the model is to attempt to model the difference between the two semiconductors, that is, the difference with respect to an chosen optimal average (whose contribution to the band offset should vanish). An example would be GaAs-AlAs, constructing it from a virtual crystal of Al_0.5Ga_0.5As, then introducing an interface. After this a perturbation is added to turn the crystal into pure GaAs, whilst on the other side, the perturbation transforms the crystal in pure AlAs. These perturbations are sufficiently small so that they can be handled by linear-response theory and the electrostatic potential lineup across the interface can then be obtained up to the first order from the charge density response to those localized perturbations. Linear response theory works well for semiconductors with similar potentials (such as GaAs-AlAs) as well as dissimilar potentials (such as GaAs-Ge), which was doubted at first. However predictions made by linear response theory coincide exactly with those of self-consistent first principle calculations. If interfaces are polar however, or nonabrupt nonpolar oriented, additional effects must be taken into account. These are additional terms which require simple electrostatics, which is within the linear response approach.

References

Franciosi A.; Van de Walle C.G: Heterojunction band offset engineering, Surface Science Reports, Volume 25, Number 1, October 1996, pp. 1–140

Raymond T. Tung; Leeor; Kronik: Charge Density and Band Offsets at Heterovalent Semiconductor Interfaces; http://onlinelibrary.wiley.com/doi/10.1002/adts.201700001/pdf

See also

• Physics

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Band offset. Read more