Categorical quantum mechanics

Categorical quantum mechanics is the study of quantum foundations and quantum information using paradigms from mathematics and computer science, notably monoidal category theory. The primitive objects of study are physical processes, and the different ways that these can be composed. It was pioneered in 2004 by Samson Abramsky and Bob Coecke. Categorical quantum mechanics is entry 18M40 in MSC2020.

Mathematical setup

Mathematically, the basic setup is captured by a dagger symmetric monoidal category: composition of morphisms models sequential composition of processes, and the tensor product describes parallel composition of processes. The role of the dagger is to assign to each state a corresponding test. These can then be adorned with more structure to study various aspects. For instance:

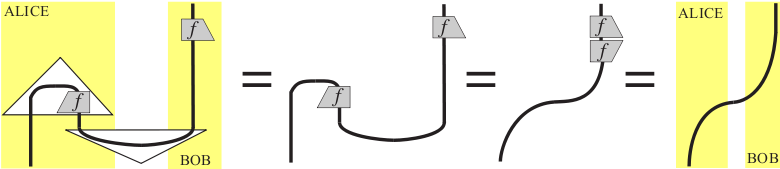
• A dagger compact category allows one to distinguish between an "input" and "output" of a process. In the diagrammatic calculus, it allows wires to be bent, allowing for a less restricted transfer of information. In particular, it allows entangled states and measurements, and gives elegant descriptions of protocols such as quantum teleportation.^[1] In quantum theory, it being compact closed is related to the Choi-Jamiołkowski isomorphism (also known as process-state duality), while the dagger structure captures the ability to take adjoints of linear maps.
• Considering only the morphisms that are completely positive maps, one can also handle mixed states, allowing the study of quantum channels categorically.^[2]
• Wires are always two-ended (and can never be split into a Y), reflecting the no-cloning and no-deleting theorems of quantum mechanics.
• Special commutative dagger Frobenius algebras model the fact that certain processes yield classical information, that can be cloned or deleted, thus capturing classical communication.^[3]
• In early works, dagger biproducts were used to study both classical communication and the superposition principle. Later, these two features have been separated.^[4]
• Complementary Frobenius algebras embody the principle of complementarity, which is used to great effect in quantum computation, as in the ZX-calculus.^[5]

A substantial portion of the mathematical backbone to this approach is drawn from 'Australian category theory', most notably from work by Max Kelly and M. L. Laplaza,^[6] Andre Joyal and Ross Street,^[7] A. Carboni and R. F. C. Walters,^[8] and Steve Lack.^[9] Modern textbooks include Categories for quantum theory^[10] and Picturing quantum processes.^[11]

Diagrammatic calculus

One of the most notable features of categorical quantum mechanics is that the compositional structure can be faithfully captured by string diagrams.^[12]

An illustration of the diagrammatic calculus: the quantum teleportation protocol as modeled in categorical quantum mechanics.

These diagrammatic languages can be traced back to Penrose graphical notation, developed in the early 1970s.^[13] Diagrammatic reasoning has been used before in quantum information science in the quantum circuit model, however, in categorical quantum mechanics primitive gates like the CNOT-gate arise as composites of more basic algebras, resulting in a much more compact calculus.^[14] In particular, the ZX-calculus has sprung forth from categorical quantum mechanics as a diagrammatic counterpart to conventional linear algebraic reasoning about quantum gates. The ZX-calculus consists of a set of generators representing the common Pauli quantum gates and the Hadamard gate equipped with a set of graphical rewrite rules governing their interaction. Although a standard set of rewrite rules has not yet been established, some versions have been proven to be complete, meaning that any equation that holds between two quantum circuits represented as diagrams can be proven using the rewrite rules.^[15] The ZX-calculus has been used to study for instance measurement-based quantum computing.

Branches of activity

Axiomatization and new models

One of the main successes of the categorical quantum mechanics research program is that from seemingly weak abstract constraints on the compositional structure, it turned out to be possible to derive many quantum mechanical phenomena. In contrast to earlier axiomatic approaches, which aimed to reconstruct Hilbert space quantum theory from reasonable assumptions, this attitude of not aiming for a complete axiomatization may lead to new interesting models that describe quantum phenomena, which could be of use when crafting future theories.^[16]

Completeness and representation results

There are several theorems relating the abstract setting of categorical quantum mechanics to traditional settings for quantum mechanics.

• Completeness of the diagrammatic calculus: an equality of morphisms can be proved in the category of finite-dimensional Hilbert spaces if and only if it can be proved in the graphical language of dagger compact closed categories.^[17]
• Dagger commutative Frobenius algebras in the category of finite-dimensional Hilbert spaces correspond to orthogonal bases.^[18] A version of this correspondence also holds in arbitrary dimension.^[19]
• Certain extra axioms guarantee that the scalars embed into the field of complex numbers, namely the existence of finite dagger biproducts and dagger equalizers, well-pointedness, and a cardinality restriction on the scalars.^[20]
• Certain extra axioms on top of the previous guarantee that a dagger symmetric monoidal category embeds into the category of Hilbert spaces, namely if every dagger monic is a dagger kernel. In that case the scalars form an involutive field instead of just embedding in one. If the category is compact, the embedding lands in finite-dimensional Hilbert spaces.^[21]
• Six axioms characterize the category of Hilbert spaces completely, fulfilling the reconstruction programme.^[22] Two of these axioms concern a dagger and a tensor product, a third concerns biproducts.
• Special dagger commutative Frobenius algebras in the category of sets and relations correspond to discrete abelian groupoids.^[23]
• Finding complementary basis structures in the category of sets and relations corresponds to solving combinatorical problems involving Latin squares.^[24]
• Dagger commutative Frobenius algebras on qubits must be either special or antispecial, relating to the fact that maximally entangled tripartite states are SLOCC-equivalent to either the GHZ or the W state.^[25]

Categorical quantum mechanics as logic

Categorical quantum mechanics can also be seen as a type theoretic form of quantum logic that, in contrast to traditional quantum logic, supports formal deductive reasoning.^[26] There exists software that supports and automates this reasoning.

There is another connection between categorical quantum mechanics and quantum logic, as subobjects in dagger kernel categories and dagger complemented biproduct categories form orthomodular lattices.^[27][28] In fact, the former setting allows logical quantifiers, the existence of which was never satisfactorily addressed in traditional quantum logic.

Categorical quantum mechanics as foundation for quantum mechanics

Categorical quantum mechanics allows a description of more general theories than quantum theory. This enables one to study which features single out quantum theory in contrast to other non-physical theories, hopefully providing some insight into the nature of quantum theory. For example, the framework allows a succinct compositional description of Spekkens' toy theory that allows one to pinpoint which structural ingredient causes it to be different from quantum theory.^[29]

Categorical quantum mechanics and DisCoCat

The DisCoCat framework applies categorical quantum mechanics to natural language processing.^[30] The types of a pregroup grammar are interpreted as quantum systems, i.e. as objects of a dagger compact category. The grammatical derivations are interpreted as quantum processes, e.g. a transitive verb takes its subject and object as input and produces a sentence as output. Function words such as determiners, prepositions, relative pronouns, coordinators, etc. can be modeled using the same Frobenius algebras that model classical communication.^[31][32] This can be understood as a monoidal functor from grammar to quantum processes, a formal analogy which led to the development of quantum natural language processing.^[33]

See also

• ZX-calculus
• String diagram
• Applied category theory
• Quantum foundations

References

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Categorical quantum mechanics. Read more