Density
Topic: Physics
 From HandWiki - Reading time: 13 min
From HandWiki - Reading time: 13 min
| Density | |
|---|---|
 A test tube holding four non-miscible colored liquids with different densities | |
Common symbols | ρ, D |
| SI unit | kg/m3 |
| Extensive? | No |
| Intensive? | Yes |
| Conserved? | No |
Derivations from other quantities | |
Density (volumetric mass density or specific mass) is the substance's mass per unit of volume. The symbol most often used for density is ρ (the lower case Greek letter rho), although the Latin letter D can also be used. Mathematically, density is defined as mass divided by volume:[1] where ρ is the density, m is the mass, and V is the volume. In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume,[2] although this is scientifically inaccurate – this quantity is more specifically called specific weight.
For a pure substance the density has the same numerical value as its mass concentration. Different materials usually have different densities, and density may be relevant to buoyancy, purity and packaging. Osmium and iridium are the densest known elements at standard conditions for temperature and pressure.
To simplify comparisons of density across different systems of units, it is sometimes replaced by the dimensionless quantity "relative density" or "specific gravity", i.e. the ratio of the density of the material to that of a standard material, usually water. Thus a relative density less than one relative to water means that the substance floats in water.
The density of a material varies with temperature and pressure. This variation is typically small for solids and liquids but much greater for gases. Increasing the pressure on an object decreases the volume of the object and thus increases its density. Increasing the temperature of a substance (with a few exceptions) decreases its density by increasing its volume. In most materials, heating the bottom of a fluid results in convection of the heat from the bottom to the top, due to the decrease in the density of the heated fluid, which causes it to rise relative to denser unheated material.
The reciprocal of the density of a substance is occasionally called its specific volume, a term sometimes used in thermodynamics. Density is an intensive property in that increasing the amount of a substance does not increase its density; rather it increases its mass.
Other conceptually comparable quantities or ratios include specific density, relative density (specific gravity), and specific weight.
History
In a well-known but probably apocryphal tale, Archimedes was given the task of determining whether King Hiero's goldsmith was embezzling gold during the manufacture of a golden wreath dedicated to the gods and replacing it with another, cheaper alloy.[3] Archimedes knew that the irregularly shaped wreath could be crushed into a cube whose volume could be calculated easily and compared with the mass; but the king did not approve of this. Baffled, Archimedes is said to have taken an immersion bath and observed from the rise of the water upon entering that he could calculate the volume of the gold wreath through the displacement of the water. Upon this discovery, he leapt from his bath and ran naked through the streets shouting, "Eureka! Eureka!" (Εύρηκα! Greek "I have found it"). As a result, the term "eureka" entered common parlance and is used today to indicate a moment of enlightenment.
The story first appeared in written form in Vitruvius' books of architecture, two centuries after it supposedly took place.[4] Some scholars have doubted the accuracy of this tale, saying among other things that the method would have required precise measurements that would have been difficult to make at the time.[5][6]
Measurement of density
A number of techniques as well as standards exist for the measurement of density of materials. Such techniques include the use of a hydrometer (a buoyancy method for liquids), Hydrostatic balance (a buoyancy method for liquids and solids), immersed body method (a buoyancy method for liquids), pycnometer (liquids and solids), air comparison pycnometer (solids), oscillating densitometer (liquids), as well as pour and tap (solids).[7] However, each individual method or technique measures different types of density (e.g. bulk density, skeletal density, etc.), and therefore it is necessary to have an understanding of the type of density being measured as well as the type of material in question.
Unit
From the equation for density (ρ = m/V), mass density has any unit that is mass divided by volume. As there are many units of mass and volume covering many different magnitudes there are a large number of units for mass density in use. The SI unit of kilogram per cubic metre (kg/m3) and the cgs unit of gram per cubic centimetre (g/cm3) are probably the most commonly used units for density. One g/cm3 is equal to 1000 kg/m3. One cubic centimetre (abbreviation cc) is equal to one millilitre. In industry, other larger or smaller units of mass and or volume are often more practical and US customary units may be used. See below for a list of some of the most common units of density.
Homogeneous materials
The density at all points of a homogeneous object equals its total mass divided by its total volume. The mass is normally measured with a scale or balance; the volume may be measured directly (from the geometry of the object) or by the displacement of a fluid. To determine the density of a liquid or a gas, a hydrometer, a dasymeter or a Coriolis flow meter may be used, respectively. Similarly, hydrostatic weighing uses the displacement of water due to a submerged object to determine the density of the object.
Heterogeneous materials
If the body is not homogeneous, then its density varies between different regions of the object. In that case the density around any given location is determined by calculating the density of a small volume around that location. In the limit of an infinitesimal volume the density of an inhomogeneous object at a point becomes: , where is an elementary volume at position . The mass of the body then can be expressed as
Non-compact materials
In practice, bulk materials such as sugar, sand, or snow contain voids. Many materials exist in nature as flakes, pellets, or granules.
Voids are regions which contain something other than the considered material. Commonly the void is air, but it could also be vacuum, liquid, solid, or a different gas or gaseous mixture.
The bulk volume of a material—inclusive of the void fraction—is often obtained by a simple measurement (e.g. with a calibrated measuring cup) or geometrically from known dimensions.
Mass divided by bulk volume determines bulk density. This is not the same thing as volumetric mass density.
To determine volumetric mass density, one must first discount the volume of the void fraction. Sometimes this can be determined by geometrical reasoning. For the close-packing of equal spheres the non-void fraction can be at most about 74%. It can also be determined empirically. Some bulk materials, however, such as sand, have a variable void fraction which depends on how the material is agitated or poured. It might be loose or compact, with more or less air space depending on handling.
In practice, the void fraction is not necessarily air, or even gaseous. In the case of sand, it could be water, which can be advantageous for measurement as the void fraction for sand saturated in water—once any air bubbles are thoroughly driven out—is potentially more consistent than dry sand measured with an air void.
In the case of non-compact materials, one must also take care in determining the mass of the material sample. If the material is under pressure (commonly ambient air pressure at the earth's surface) the determination of mass from a measured sample weight might need to account for buoyancy effects due to the density of the void constituent, depending on how the measurement was conducted. In the case of dry sand, sand is so much denser than air that the buoyancy effect is commonly neglected (less than one part in one thousand).
Mass change upon displacing one void material with another while maintaining constant volume can be used to estimate the void fraction, if the difference in density of the two voids materials is reliably known.
Changes of density
In general, density can be changed by changing either the pressure or the temperature. Increasing the pressure always increases the density of a material. Increasing the temperature generally decreases the density, but there are notable exceptions to this generalization. For example, the density of water increases between its melting point at 0 °C and 4 °C; similar behavior is observed in silicon at low temperatures.
The effect of pressure and temperature on the densities of liquids and solids is small. The compressibility for a typical liquid or solid is 10−6 bar−1 (1 bar = 0.1 MPa) and a typical thermal expansivity is 10−5 K−1. This roughly translates into needing around ten thousand times atmospheric pressure to reduce the volume of a substance by one percent. (Although the pressures needed may be around a thousand times smaller for sandy soil and some clays.) A one percent expansion of volume typically requires a temperature increase on the order of thousands of degrees Celsius.
In contrast, the density of gases is strongly affected by pressure. The density of an ideal gas is
where M is the molar mass, P is the pressure, R is the universal gas constant, and T is the absolute temperature. This means that the density of an ideal gas can be doubled by doubling the pressure, or by halving the absolute temperature.
In the case of volumic thermal expansion at constant pressure and small intervals of temperature the temperature dependence of density is
where is the density at a reference temperature, is the thermal expansion coefficient of the material at temperatures close to .
Density of solutions
The density of a solution is the sum of mass (massic) concentrations of the components of that solution.
Mass (massic) concentration of each given component in a solution sums to density of the solution,
Expressed as a function of the densities of pure components of the mixture and their volume participation, it allows the determination of excess molar volumes: provided that there is no interaction between the components.
Knowing the relation between excess volumes and activity coefficients of the components, one can determine the activity coefficients:
Densities
Various materials
| Material | ρ (kg/m3)[note 1] | Notes |
|---|---|---|
| Hydrogen | 0.0898 | |
| Helium | 0.179 | |
| Aerographite | 0.2 | [note 2][8][9] |
| Metallic microlattice | 0.9 | [note 2] |
| Aerogel | 1.0 | [note 2] |
| Air | 1.2 | At sea level |
| Tungsten hexafluoride | 12.4 | One of the heaviest known gases at standard conditions |
| Liquid hydrogen | 70 | At approximately −255 °C |
| Styrofoam | 75 | Approximate[10] |
| Cork | 240 | Approximate[10] |
| Pine | 373 | [11] |
| Lithium | 535 | Least dense metal |
| Wood | 700 | Seasoned, typical[12][13] |
| Oak | 710 | [11] |
| Potassium | 860 | [14] |
| Ice | 916.7 | At temperature < 0 °C |
| Cooking oil | 910–930 | |
| Sodium | 970 | |
| Water (fresh) | 1,000 | At 4 °C, the temperature of its maximum density |
| Water (salt) | 1,030 | 3% |
| Liquid oxygen | 1,141 | At approximately −219 °C |
| Nylon | 1,150 | |
| Plastics | 1,175 | Approximate; for polypropylene and PETE/PVC |
| Glycerol | 1,261 | [15] |
| Tetrachloroethene | 1,622 | |
| Sand | 1,600 | Between 1,600 and 2000 [16] |
| Magnesium | 1,740 | |
| Beryllium | 1,850 | |
| Silicon | 2,330 | |
| Concrete | 2,400 | [17][18] |
| Glass | 2,500 | [19] |
| Quartzite | 2,600 | [16] |
| Granite | 2,700 | [16] |
| Gneiss | 2,700 | [16] |
| Aluminium | 2,700 | |
| Limestone | 2,750 | Compact[16] |
| Basalt | 3,000 | [16] |
| Diiodomethane | 3,325 | Liquid at room temperature |
| Diamond | 3,500 | |
| Titanium | 4,540 | |
| Selenium | 4,800 | |
| Vanadium | 6,100 | |
| Antimony | 6,690 | |
| Zinc | 7,000 | |
| Chromium | 7,200 | |
| Tin | 7,310 | |
| Manganese | 7,325 | Approximate |
| Iron | 7,870 | |
| Mild steel | 7,850 | |
| Niobium | 8,570 | |
| Brass | 8,600 | [18] |
| Cadmium | 8,650 | |
| Cobalt | 8,900 | |
| Nickel | 8,900 | |
| Copper | 8,940 | |
| Bismuth | 9,750 | |
| Molybdenum | 10,220 | |
| Silver | 10,500 | |
| Lead | 11,340 | |
| Thorium | 11,700 | |
| Rhodium | 12,410 | |
| Mercury | 13,546 | |
| Tantalum | 16,600 | |
| Uranium | 19,100 | |
| Tungsten | 19,300 | |
| Gold | 19,320 | |
| Plutonium | 19,840 | |
| Rhenium | 21,020 | |
| Platinum | 21,450 | |
| Iridium | 22,420 | |
| Osmium | 22,570 | Densest natural element on Earth |
Others
| Entity | ρ (kg/m3) | Notes |
|---|---|---|
| Interstellar medium | 1.7×10−26 | Based on 10−5 hydrogen atoms per cubic centimetre[20] |
| Local Interstellar Cloud | 5×10−22 | Based on 0.3 hydrogen atoms per cubic centimetre[20] |
| Interstellar medium | 1.7×10−16 | Based on 105 hydrogen atoms per cubic centimetre[20] |
| The Earth | 5,515 | Mean density.[21] |
| Earth's inner core | 13,000 | Approx., as listed in Earth.[22] |
| The core of the Sun | 33,000–160,000 | Approx.[23] |
| White dwarf star | 2.1×109 | Approx.[24] |
| Atomic nuclei | 2.3×1017 | Does not depend strongly on size of nucleus[25] |
| Neutron star | 1×1018 |
Water
| Temp. (°C)[note 1] | Density (kg/m3) |
|---|---|
| −30 | 983.854 |
| −20 | 993.547 |
| −10 | 998.117 |
| 0 | 999.8395 |
| 4 | 999.9720 |
| 10 | 999.7026 |
| 15 | 999.1026 |
| 20 | 998.2071 |
| 22 | 997.7735 |
| 25 | 997.0479 |
| 30 | 995.6502 |
| 40 | 992.2 |
| 60 | 983.2 |
| 80 | 971.8 |
| 100 | 958.4 |
Notes:
| |
Air
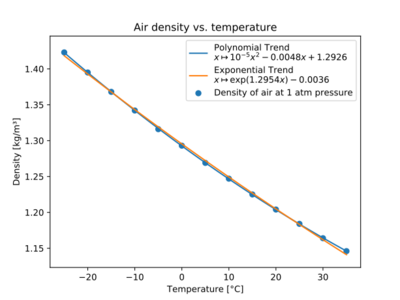
| T (°C) | ρ (kg/m3) |
|---|---|
| −25 | 1.423 |
| −20 | 1.395 |
| −15 | 1.368 |
| −10 | 1.342 |
| −5 | 1.316 |
| 0 | 1.293 |
| 5 | 1.269 |
| 10 | 1.247 |
| 15 | 1.225 |
| 20 | 1.204 |
| 25 | 1.184 |
| 30 | 1.164 |
| 35 | 1.146 |
Molar volumes of liquid and solid phase of elements

Common units
The SI unit for density is:
- kilogram per cubic metre (kg/m3)
The litre and tonne are not part of the SI, but are acceptable for use with it, leading to the following units:
Densities using the following metric units all have exactly the same numerical value, one thousandth of the value in (kg/m3). Liquid water has a density of about 1 kg/dm3, making any of these SI units numerically convenient to use as most solids and liquids have densities between 0.1 and 20 kg/dm3.
- kilogram per cubic decimetre (kg/dm3)
- gram per cubic centimetre (g/cm3)
- 1 g/cm3 = 1000 kg/m3
- megagram (metric ton) per cubic metre (Mg/m3)
In US customary units density can be stated in:
- Avoirdupois ounce per cubic inch (1 g/cm3 ≈ 0.578036672 oz/cu in)
- Avoirdupois ounce per fluid ounce (1 g/cm3 ≈ 1.04317556 oz/US fl oz = 1.04317556 lb/US fl pint)
- Avoirdupois pound per cubic inch (1 g/cm3 ≈ 0.036127292 lb/cu in)
- pound per cubic foot (1 g/cm3 ≈ 62.427961 lb/cu ft)
- pound per cubic yard (1 g/cm3 ≈ 1685.5549 lb/cu yd)
- pound per US liquid gallon (1 g/cm3 ≈ 8.34540445 lb/US gal)
- pound per US bushel (1 g/cm3 ≈ 77.6888513 lb/bu)
- slug per cubic foot
Imperial units differing from the above (as the Imperial gallon and bushel differ from the US units) in practice are rarely used, though found in older documents. The Imperial gallon was based on the concept that an Imperial fluid ounce of water would have a mass of one Avoirdupois ounce, and indeed 1 g/cm3 ≈ 1.00224129 ounces per Imperial fluid ounce = 10.0224129 pounds per Imperial gallon. The density of precious metals could conceivably be based on Troy ounces and pounds, a possible cause of confusion.
Knowing the volume of the unit cell of a crystalline material and its formula weight (in daltons), the density can be calculated. One dalton per cubic ångström is equal to a density of 1.660 539 066 60 g/cm3.
See also
- Densities of the elements (data page)
- List of elements by density
- Air density
- Area density
- Bulk density
- Buoyancy
- Charge density
- Density prediction by the Girolami method
- Dord
- Energy density
- Lighter than air
- Linear density
- Number density
- Orthobaric density
- Paper density
- Specific weight
- Spice (oceanography)
- Standard temperature and pressure
References
- ↑ The National Aeronautic and Atmospheric Administration's Glenn Research Center. "Gas Density Glenn research Center". grc.nasa.gov. http://www.grc.nasa.gov/WWW/BGH/fluden.html.
- ↑ "Density definition in Oil Gas Glossary". Oilgasglossary.com. http://oilgasglossary.com/density.html.
- ↑ Archimedes, A Gold Thief and Buoyancy – by Larry "Harris" Taylor, Ph.D.
- ↑ Vitruvius on Architecture, Book IX, paragraphs 9–12, translated into English and in the original Latin.
- ↑ "EXHIBIT: The First Eureka Moment". Science 305 (5688): 1219e. 2004. doi:10.1126/science.305.5688.1219e.
- ↑ Biello, David (2006-12-08). "Fact or Fiction?: Archimedes Coined the Term "Eureka!" in the Bath". Scientific American. https://www.scientificamerican.com/article/fact-or-fiction-archimede.
- ↑ "Test No. 109: Density of Liquids and Solids". OECD Guidelines for the Testing of Chemicals, Section 1: 6. 2 October 2012. doi:10.1787/9789264123298-en. ISBN 9789264123298. ISSN 2074-5753.
- ↑ New carbon nanotube struructure aerographite is lightest material champ . Phys.org (July 13, 2012). Retrieved on July 14, 2012.
- ↑ Aerographit: Leichtestes Material der Welt entwickelt – SPIEGEL ONLINE . Spiegel.de (July 11, 2012). Retrieved on July 14, 2012.
- ↑ 10.0 10.1 "Re: which is more bouyant [sic] styrofoam or cork". Madsci.org. http://www.madsci.org/posts/archives/mar2000/954534602.Ph.r.html.
- ↑ 11.0 11.1 Serway, Raymond; Jewett, John (2005), Principles of Physics: A Calculus-Based Text, Cengage Learning, p. 467, ISBN 0-534-49143-X, https://books.google.com/books?id=VaroJ5BNuZAC
- ↑ "Wood Densities". www.engineeringtoolbox.com. http://www.engineeringtoolbox.com/wood-density-d_40.html.
- ↑ "Density of Wood". www.simetric.co.uk. http://www.simetric.co.uk/si_wood.htm.
- ↑ Bolz, Ray E.; Tuve, George L., eds (1970). "§1.3 Solids—Metals: Table 1-59 Metals and Alloys—Miscellaneous Properties". CRC Handbook of tables for Applied Engineering Science (2nd ed.). CRC Press. pp. 117. ISBN 9781315214092. https://books.google.com/books?id=Xn8KbsgeFrwC&pg=PA117.
- ↑ glycerol composition at . Physics.nist.gov. Retrieved on July 14, 2012.
- ↑ 16.0 16.1 16.2 16.3 16.4 16.5 Sharma, P.V. (1997), Environmental and Engineering Geophysics, Cambridge University Press, p. 17, doi:10.1017/CBO9781139171168, ISBN 9781139171168
- ↑ "Density of Concrete - The Physics Factbook". https://hypertextbook.com/facts/1999/KatrinaJones.shtml.
- ↑ 18.0 18.1 Young, Hugh D.; Freedman, Roger A. (2012). University Physics with Modern Physics. Addison-Wesley. pp. 374. ISBN 978-0-321-69686-1.
- ↑ "Density of Glass - The Physics Factbook". https://hypertextbook.com/facts/2004/ShayeStorm.shtml.
- ↑ 20.0 20.1 20.2 "Our Local Galactic Neighborhood". NASA. 2000. http://interstellar.jpl.nasa.gov/interstellar/probe/introduction/neighborhood.html.
- ↑ Density of the Earth, wolframalpha.com, http://www.wolframalpha.com/input/?i=density+of+the+earth
- ↑ Density of Earth's core, wolframalpha.com, http://www.wolframalpha.com/input/?i=density+of+earth%27s+core
- ↑ Density of the Sun's core, wolframalpha.com, http://www.wolframalpha.com/input/?i=density+of+sun%27s+core
- ↑ Johnson, Jennifer. "Extreme Stars: White Dwarfs & Neutron Stars"]. lecture notes, Astronomy 162. Ohio State University. http://www.astronomy.ohio-state.edu/~jaj/Ast162/lectures/notesWL22.pdf.
- ↑ "Nuclear Size and Density". HyperPhysics. Georgia State University. http://hyperphysics.phy-astr.gsu.edu/HBASE/Nuclear/nucuni.html.
External links
 "Density". The New Student's Reference Work. 1914.
"Density". The New Student's Reference Work. 1914.- Video: Density Experiment with Oil and Alcohol
- Video: Density Experiment with Whiskey and Water
- Glass Density Calculation – Calculation of the density of glass at room temperature and of glass melts at 1000 – 1400°C
- List of Elements of the Periodic Table – Sorted by Density
- Calculation of saturated liquid densities for some components
- Field density test
- Water – Density and specific weight
- Temperature dependence of the density of water – Conversions of density units
- A delicious density experiment
- Water density calculator Water density for a given salinity and temperature.
- Liquid density calculator Select a liquid from the list and calculate density as a function of temperature.
- Gas density calculator Calculate density of a gas for as a function of temperature and pressure.
- Densities of various materials.
- Determination of Density of Solid, instructions for performing classroom experiment.
- "A model for calculating the density of aqueous multicomponent electrolyte solutions". Journal of the Chilean Chemical Society 53 (1): 1393–8. 2008. doi:10.4067/S0717-97072008000100015.
- "Derived thermodynamic properties of alcohol+ cyclohexylamine mixtures". Journal of the Serbian Chemical Society 75 (2): 283–293. 2010. doi:10.2298/JSC1002283R.
 KSF
KSF