Electrodynamic tether
Topic: Physics
 From HandWiki - Reading time: 34 min
From HandWiki - Reading time: 34 min

Electrodynamic tethers (EDTs) are long conducting wires, such as one deployed from a tether satellite, which can operate on electromagnetic principles as generators, by converting their kinetic energy to electrical energy, or as motors, converting electrical energy to kinetic energy.[1] Electric potential is generated across a conductive tether by its motion through a planet's magnetic field.
A number of missions have demonstrated electrodynamic tethers in space, most notably the TSS-1, TSS-1R, and Plasma Motor Generator (PMG) experiments.
Tether propulsion
As part of a tether propulsion system, craft can use long, strong conductors (though not all tethers are conductive) to change the orbits of spacecraft. It has the potential to make space travel significantly cheaper.[citation needed] When direct current is applied to the tether, it exerts a Lorentz force against the magnetic field, and the tether exerts a force on the vehicle. It can be used either to accelerate or brake an orbiting spacecraft.
In 2012 Star Technology and Research was awarded a $1.9 million contract to qualify a tether propulsion system for orbital debris removal.[2]
Uses for ED tethers
Over the years, numerous applications for electrodynamic tethers have been identified for potential use in industry, government, and scientific exploration. The table below is a summary of some of the potential applications proposed thus far. Some of these applications are general concepts, while others are well-defined systems. Many of these concepts overlap into other areas; however, they are simply placed under the most appropriate heading for the purposes of this table. All of the applications mentioned in the table are elaborated upon in the Tethers Handbook.[1] Three fundamental concepts that tethers possess, are gravity gradients, momentum exchange, and electrodynamics. Potential tether applications can be seen below:
| ELECTRODYNAMICS | |
|---|---|
| Electrodynamic power generation | Electrodynamic thrust generation |
| ULF/ELF/VLF communication antenna | Radiation belt remediation |
| SPACE STATION | |
| Microgravity laboratory | Shuttle de-orbit from Space Station |
| Tethered Space Transfer Vehicle (STV) launch | Variable/low gravity laboratory |
| Attitude stabilization and control | ISS reboost |
| TRANSPORTATION | |
| Generalized momentum scavenging spent stages | Internal forces for orbital modification |
| Satellite boost from orbiter | Tether Assisted Transportation System (TATS) |
| Tether re-boosting of decaying satellites | Upper stage boost from Orbiter |
ISS reboost
EDT has been proposed to maintain the ISS orbit and save the expense of chemical propellant reboosts.[3] It could improve the quality and duration of microgravity conditions.[3]
Electrodynamic tether fundamentals

The choice of the metal conductor to be used in an electrodynamic tether is determined by a variety of factors. Primary factors usually include high electrical conductivity, and low density. Secondary factors, depending on the application, include cost, strength, and melting point.
An electromotive force (EMF) is generated across a tether element as it moves relative to a magnetic field. The force is given by Faraday's Law of Induction:
Without loss of generality, it is assumed the tether system is in Earth orbit and it moves relative to Earth's magnetic field. Similarly, if current flows in the tether element, a force can be generated in accordance with the Lorentz force equation
In self-powered mode (deorbit mode), this EMF can be used by the tether system to drive the current through the tether and other electrical loads (e.g. resistors, batteries), emit electrons at the emitting end, or collect electrons at the opposite. In boost mode, on-board power supplies must overcome this motional EMF to drive current in the opposite direction, thus creating a force in the opposite direction, as seen in below figure, and boosting the system.
Take, for example, the NASA Propulsive Small Expendable Deployer System (ProSEDS) mission as seen in above figure.[4][5][6][7][8] At 300 km altitude, the Earth's magnetic field, in the north-south direction, is approximately 0.18–0.32 gauss up to ~40° inclination, and the orbital velocity with respect to the local plasma is about 7500 m/s. This results in a Vemf range of 35–250 V/km along the 5 km length of tether. This EMF dictates the potential difference across the bare tether which controls where electrons are collected and / or repelled. Here, the ProSEDS de-boost tether system is configured to enable electron collection to the positively biased higher altitude section of the bare tether, and returned to the ionosphere at the lower altitude end. This flow of electrons through the length of the tether in the presence of the Earth's magnetic field creates a force that produces a drag thrust that helps de-orbit the system, as given by the above equation. The boost mode is similar to the de-orbit mode, except for the fact that a High Voltage Power Supply (HVPS) is also inserted in series with the tether system between the tether and the higher positive potential end. The power supply voltage must be greater than the EMF and the polar opposite. This drives the current in the opposite direction, which in turn causes the higher altitude end to be negatively charged, while the lower altitude end is positively charged(Assuming a standard east to west orbit around Earth).
To further emphasize the de-boosting phenomenon, a schematic sketch of a bare tether system with no insulation (all bare) can be seen in below figure.

The top of the diagram, point A, represents the electron collection end. The bottom of the tether, point C, is the electron emission end. Similarly, and represent the potential difference from their respective tether ends to the plasma, and is the potential anywhere along the tether with respect to the plasma. Finally, point B is the point at which the potential of the tether is equal to the plasma. The location of point B will vary depending on the equilibrium state of the tether, which is determined by the solution of Kirchhoff's voltage law (KVL)
and Kirchhoff's current law (KCL)
along the tether. Here , , and describe the current gain from point A to B, the current lost from point B to C, and the current lost at point C, respectively.
Since the current is continuously changing along the bare length of the tether, the potential loss due to the resistive nature of the wire is represented as . Along an infinitesimal section of tether, the resistance multiplied by the current traveling across that section is the resistive potential loss.
After evaluating KVL & KCL for the system, the results will yield a current and potential profile along the tether, as seen in above figure. This diagram shows that, from point A of the tether down to point B, there is a positive potential bias, which increases the collected current. Below that point, the becomes negative and the collection of ion current begins. Since it takes a much greater potential difference to collect an equivalent amount of ion current (for a given area), the total current in the tether is reduced by a smaller amount. Then, at point C, the remaining current in the system is drawn through the resistive load (), and emitted from an electron emissive device (), and finally across the plasma sheath (). The KVL voltage loop is then closed in the ionosphere where the potential difference is effectively zero.
Due to the nature of the bare EDTs, it is often not optional to have the entire tether bare. In order to maximize the thrusting capability of the system a significant portion of the bare tether should be insulated. This insulation amount depends on a number of effects, some of which are plasma density, the tether length and width, the orbiting velocity, and the Earth's magnetic flux density.
Tethers as generators

An electrodynamic tether is attached to an object, the tether being oriented at an angle to the local vertical between the object and a planet with a magnetic field. The tether's far end can be left bare, making electrical contact with the ionosphere. When the tether intersects the planet's magnetic field, it generates a current, and thereby converts some of the orbiting body's kinetic energy to electrical energy. Functionally, electrons flow from the space plasma into the conductive tether, are passed through a resistive load in a control unit and are emitted into the space plasma by an electron emitter as free electrons. As a result of this process, an electrodynamic force acts on the tether and attached object, slowing their orbital motion. In a loose sense, the process can be likened to a conventional windmill- the drag force of a resistive medium (air or, in this case, the magnetosphere) is used to convert the kinetic energy of relative motion (wind, or the satellite's momentum) into electricity. In principle, compact high-current tether power generators are possible and, with basic hardware, tens, hundreds, and thousands of kilowatts appears to be attainable.[10]
Voltage and current
NASA has conducted several experiments with Plasma Motor Generator (PMG) tethers in space. An early experiment used a 500-meter conducting tether. In 1996, NASA conducted an experiment with a 20,000-meter conducting tether. When the tether was fully deployed during this test, the orbiting tether generated a potential of 3,500 volts. This conducting single-line tether was severed after five hours of deployment. It is believed that the failure was caused by an electric arc generated by the conductive tether's movement through the Earth's magnetic field.[11]
When a tether is moved at a velocity (v) at right angles to the Earth's magnetic field (B), an electric field is observed in the tether's frame of reference. This can be stated as:
- E = v * B = vB
The direction of the electric field (E) is at right angles to both the tether's velocity (v) and magnetic field (B). If the tether is a conductor, then the electric field leads to the displacement of charges along the tether. Note that the velocity used in this equation is the orbital velocity of the tether. The rate of rotation of the Earth, or of its core, is not relevant. In this regard, see also homopolar generator.
Voltage across conductor
With a long conducting wire of length L, an electric field E is generated in the wire. It produces a voltage V between the opposite ends of the wire. This can be expressed as:
where the angle τ is between the length vector (L) of the tether and the electric field vector (E), assumed to be in the vertical direction at right angles to the velocity vector (v) in plane and the magnetic field vector (B) is out of the plane.
Current in conductor
An electrodynamic tether can be described as a type of thermodynamically "open system". Electrodynamic tether circuits cannot be completed by simply using another wire, since another tether will develop a similar voltage. Fortunately, the Earth's magnetosphere is not "empty", and, in near-Earth regions (especially near the Earth's atmosphere) there exist highly electrically conductive plasmas which are kept partially ionized by solar radiation or other radiant energy. The electron and ion density varies according to various factors, such as the location, altitude, season, sunspot cycle, and contamination levels. It is known that a positively charged bare conductor can readily remove free electrons out of the plasma. Thus, to complete the electrical circuit, a sufficiently large area of uninsulated conductor is needed at the upper, positively charged end of the tether, thereby permitting current to flow through the tether.
However, it is more difficult for the opposite (negative) end of the tether to eject free electrons or to collect positive ions from the plasma. It is plausible that, by using a very large collection area at one end of the tether, enough ions can be collected to permit significant current through the plasma. This was demonstrated during the Shuttle orbiter's TSS-1R mission, when the shuttle itself was used as a large plasma contactor to provide over an ampere of current. Improved methods include creating an electron emitter, such as a thermionic cathode, plasma cathode, plasma contactor, or field electron emission device. Since both ends of the tether are "open" to the surrounding plasma, electrons can flow out of one end of the tether while a corresponding flow of electrons enters the other end. In this fashion, the voltage that is electromagnetically induced within the tether can cause current to flow through the surrounding space environment, completing an electrical circuit through what appears to be, at first glance, an open circuit.
Tether current
The amount of current (I) flowing through a tether depends on various factors. One of these is the circuit's total resistance (R). The circuit's resistance consist of three components:
- the effective resistance of the plasma,
- the resistance of the tether, and
- a control variable resistor.
In addition, a parasitic load is needed. The load on the current may take the form of a charging device which, in turn, charges reserve power sources such as batteries. The batteries in return will be used to control power and communication circuits, as well as drive the electron emitting devices at the negative end of the tether. As such the tether can be completely self-powered, besides the initial charge in the batteries to provide electrical power for the deployment and startup procedure.
The charging battery load can be viewed as a resistor which absorbs power, but stores this for later use (instead of immediately dissipating heat). It is included as part of the "control resistor". The charging battery load is not treated as a "base resistance" though, as the charging circuit can be turned off at any time. When off, the operations can be continued without interruption using the power stored in the batteries.
Current collection / emission for an EDT system: theory and technology
Understanding electron and ion current collection to and from the surrounding ambient plasma is critical for most EDT systems. Any exposed conducting section of the EDT system can passively ('passive' and 'active' emission refers to the use of pre-stored energy in order to achieve the desired effect) collect electron or ion current, depending on the electric potential of the spacecraft body with respect to the ambient plasma. In addition, the geometry of the conducting body plays an important role in the size of the sheath and thus the total collection capability. As a result, there are a number of theories for the varying collection techniques.
The primary passive processes that control the electron and ion collection on an EDT system are thermal current collection, ion ram collection effects, electron photoemission, and possibly secondary electron and ion emission. In addition, the collection along a thin bare tether is described using orbital motion limited (OML) theory as well as theoretical derivations from this model depending on the physical size with respect to the plasma Debye length. These processes take place all along the exposed conducting material of the entire system. Environmental and orbital parameters can significantly influence the amount collected current. Some important parameters include plasma density, electron and ion temperature, ion molecular weight, magnetic field strength and orbital velocity relative to the surrounding plasma.
Then there are active collection and emission techniques involved in an EDT system. This occurs through devices such as hollow cathode plasma contactors, thermionic cathodes, and field emitter arrays. The physical design of each of these structures as well as the current emission capabilities are thoroughly discussed.
Bare conductive tethers
The concept of current collection to a bare conducting tether was first formalized by Sanmartin and Martinez-Sanchez.[9] They note that the most area efficient current collecting cylindrical surface is one that has an effective radius less than ~1 Debye length where current collection physics is known as orbital motion limited (OML) in a collisionless plasma. As the effective radius of the bare conductive tether increases past this point then there are predictable reductions in collection efficiency compared to OML theory. In addition to this theory (which has been derived for a non-flowing plasma), current collection in space occurs in a flowing plasma, which introduces another collection effect. These issues are explored in greater detail below.
Orbit motion limited (OML) theory
The electron Debye length[13] is defined as the characteristic shielding distance in a plasma, and is described by the equation
This distance, where all electric fields in the plasma resulting from the conductive body have fallen off by 1/e, can be calculated. OML theory[14] is defined with the assumption that the electron Debye length is equal to or larger than the size of the object and the plasma is not flowing. The OML regime occurs when the sheath becomes sufficiently thick such that orbital effects become important in particle collection. This theory accounts for and conserves particle energy and angular momentum. As a result, not all particles that are incident onto the surface of the thick sheath are collected. The voltage of the collecting structure with respect to the ambient plasma, as well as the ambient plasma density and temperature, determines the size of the sheath. This accelerating (or decelerating) voltage combined with the energy and momentum of the incoming particles determines the amount of current collected across the plasma sheath.
The orbital-motion-limit regime is attained when the cylinder radius is small enough such that all incoming particle trajectories that are collected are terminated on the cylinder's surface are connected to the background plasma, regardless of their initial angular momentum (i.e., none are connected to another location on the probe's surface). Since, in a quasi-neutral collisionless plasma, the distribution function is conserved along particle orbits, having all “directions of arrival” populated corresponds to an upper limit on the collected current per unit area (not total current).[15]
In an EDT system, the best performance for a given tether mass is for a tether diameter chosen to be smaller than an electron Debye length for typical ionospheric ambient conditions (Typical ionospheric conditions in the from 200 to 2000 km altitude range, have a T_e ranging from 0.1 eV to 0.35 eV, and n_e ranging from 10^10 m^-3 to 10^12 m^-3 ), so it is therefore within the OML regime. Tether geometries outside this dimension have been addressed.[16] OML collection will be used as a baseline when comparing the current collection results for various sample tether geometries and sizes.
In 1962 Gerald H. Rosen derived the equation that is now known as the OML theory of dust charging.[17] According to Robert Merlino of the University of Iowa, Rosen seems to have arrived at the equation 30 years before anyone else.[18]
Deviations from OML theory in a non-flowing plasma
For a variety of practical reasons, current collection to a bare EDT does not always satisfy the assumption of OML collection theory. Understanding how the predicted performance deviates from theory is important for these conditions. Two commonly proposed geometries for an EDT involve the use of a cylindrical wire and a flat tape. As long as the cylindrical tether is less than one Debye length in radius, it will collect according to the OML theory. However, once the width exceeds this distance, then the collection increasingly deviates from this theory. If the tether geometry is a flat tape, then an approximation can be used to convert the normalized tape width to an equivalent cylinder radius. This was first done by Sanmartin and Estes[19] and more recently using the 2-Dimensional Kinetic Plasma Solver (KiPS 2-D) by Choiniere et al.[15]
Flowing plasma effect
There is at present, no closed-form solution to account for the effects of plasma flow relative to the bare tether. However, numerical simulation has been recently developed by Choiniere et al. using KiPS-2D which can simulate flowing cases for simple geometries at high bias potentials.[20][21] This flowing plasma analysis as it applies to EDTs have been discussed.[16] This phenomenon is presently being investigated through recent work, and is not fully understood.
Endbody collection
This section discusses the plasma physics theory that explains passive current collection to a large conductive body which will be applied at the end of an ED tether. When the size of the sheath is much smaller than the radius of the collecting body then depending on the polarity of the difference between the potential of the tether and that of the ambient plasma, (V – Vp), it is assumed that all of the incoming electrons or ions that enter the plasma sheath are collected by the conductive body.[13][15] This 'thin sheath' theory involving non-flowing plasmas is discussed, and then the modifications to this theory for flowing plasma is presented. Other current collection mechanisms will then be discussed. All of the theory presented is used towards developing a current collection model to account for all conditions encountered during an EDT mission.
Passive collection theory
In a non-flowing quasi-neutral plasma with no magnetic field, it can be assumed that a spherical conducting object will collect equally in all directions. The electron and ion collection at the end-body is governed by the thermal collection process, which is given by Ithe and Ithi.[22]
Flowing plasma electron collection mode
The next step in developing a more realistic model for current collection is to include the magnetic field effects and plasma flow effects. Assuming a collisionless plasma, electrons and ions gyrate around magnetic field lines as they travel between the poles around the Earth due to magnetic mirroring forces and gradient-curvature drift.[23] They gyrate at a particular radius and frequency dependence upon their mass, the magnetic field strength, and energy. These factors must be considered in current collection models.
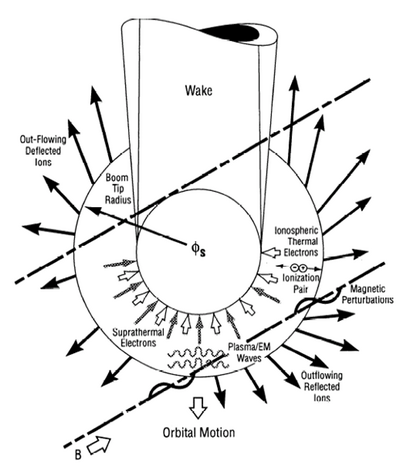
Flowing plasma ion collection model
When the conducting body is negatively biased with respect to the plasma and traveling above the ion thermal velocity, there are additional collection mechanisms at work. For typical Low Earth Orbits (LEOs), between 200 km and 2000 km,[25] the velocities in an inertial reference frame range from 7.8 km/s to 6.9 km/s for a circular orbit and the atmospheric molecular weights range from 25.0 amu (O+, O2+, & NO+) to 1.2 amu (mostly H+), respectively.[26][27][28] Assuming that the electron and ion temperatures range from ~0.1 eV to 0.35 eV, the resulting ion velocity ranges from 875 m/s to 4.0 km/s from 200 km to 2000 km altitude, respectively. The electrons are traveling at approximately 188 km/s throughout LEO. This means that the orbiting body is traveling faster than the ions and slower than the electrons, or at a mesosonic speed. This results in a unique phenomenon whereby the orbiting body 'rams' through the surrounding ions in the plasma creating a beam like effect in the reference frame of the orbiting body.
Porous endbodies
Porous endbodies have been proposed as a way to reduce the drag of a collecting endbody while ideally maintaining a similar current collection. They are often modeled as solid endbodies, except they are a small percentage of the solid spheres surface area. This is, however, an extreme oversimplification of the concept. Much has to be learned about the interactions between the sheath structure, the geometry of the mesh, the size of the endbody, and its relation to current collection. This technology also has the potential to resolve a number of issues concerning EDTs. Diminishing returns with collection current and drag area have set a limit that porous tethers might be able to overcome. Work has been accomplished on current collection using porous spheres, by Stone et al.[29][30] and Khazanov et al.[31]
It has been shown that the maximum current collected by a grid sphere compared to the mass and drag reduction can be estimated. The drag per unit of collected current for a grid sphere with a transparency of 80 to 90% is approximately 1.2 – 1.4 times smaller than that of a solid sphere of the same radius. The reduction in mass per unit volume, for this same comparison, is 2.4 – 2.8 times.[31]
Other current collection methods
In addition to the electron thermal collection, other processes that could influence the current collection in an EDT system are photoemission, secondary electron emission, and secondary ion emission. These effects pertain to all conducting surfaces on an EDT system, not just the end-body.
Space charge limits across plasma sheaths
In any application where electrons are emitted across a vacuum gap, there is a maximum allowable current for a given bias due to the self repulsion of the electron beam. This classical 1-D space charge limit (SCL) is derived for charged particles of zero initial energy, and is termed the Child-Langmuir Law.[32][33][34] This limit depends on the emission surface area, the potential difference across the plasma gap and the distance of that gap. Further discussion of this topic can be found.[35][36][37][38]
Electron emitters
There are three active electron emission technologies usually considered for EDT applications: hollow cathode plasma contactors (HCPCs), thermionic cathodes (TCs), and field emission cathodes (FEC), often in the form of field emitter arrays (FEAs). System level configurations will be presented for each device, as well as the relative costs, benefits, and validation.
Thermionic cathode (TC)
Thermionic emission is the flow of electrons from a heated charged metal or metal oxide surface, caused by thermal vibrational energy overcoming the work function (electrostatic forces holding electrons to the surface). The thermionic emission current density, J, rises rapidly with increasing temperature, releasing a significant number of electrons into the vacuum near the surface. The quantitative relation is given in the equation
This equation is called the Richardson-Dushman or Richardson equation. (ф is approximately 4.54 eV and AR ~120 A/cm2 for tungsten).[39]
Once the electrons are thermionically emitted from the TC surface they require an acceleration potential to cross a gap, or in this case, the plasma sheath. Electrons can attain this necessary energy to escape the SCL of the plasma sheath if an accelerated grid, or electron gun, is used. The equation
shows what potential is needed across the grid in order to emit a certain current entering the device.[40][41]
Here, η is the electron gun assembly (EGA) efficiency (~0.97 in TSS-1), ρ is the perveance of the EGA (7.2 micropervs in TSS-1), ΔVtc is the voltage across the accelerating grid of the EGA, and It is the emitted current.[40] The perveance defines the space charge limited current that can be emitted from a device. The figure below displays commercial examples of thermionic emitters and electron guns produced at Heatwave Labs Inc.

TC electron emission will occur in one of two different regimes: temperature or space charge limited current flow. For temperature limited flow every electron that obtains enough energy to escape from the cathode surface is emitted, assuming the acceleration potential of the electron gun is large enough. In this case, the emission current is regulated by the thermionic emission process, given by the Richardson Dushman equation. In SCL electron current flow there are so many electrons emitted from the cathode that not all of them are accelerated enough by the electron gun to escape the space charge. In this case, the electron gun acceleration potential limits the emission current. The below chart displays the temperature limiting currents and SCL effects. As the beam energy of the electrons is increased, the total escaping electrons can be seen to increase. The curves that become horizontal are temperature limited cases.

Field emission cathode (FEC)
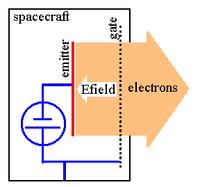
In field electron emission, electrons tunnel through a potential barrier, rather than escaping over it as in thermionic emission or photoemission.[43] For a metal at low temperature, the process can be understood in terms of the figure below. The metal can be considered a potential box, filled with electrons to the Fermi level (which lies below the vacuum level by several electron volts). The vacuum level represents the potential energy of an electron at rest outside the metal in the absence of an external field. In the presence of a strong electric field, the potential outside the metal will be deformed along the line AB, so that a triangular barrier is formed, through which electrons can tunnel. Electrons are extracted from the conduction band with a current density given by the Fowler−Nordheim equation
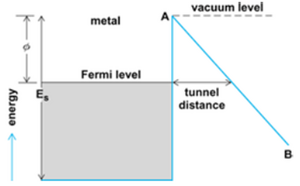
AFN and BFN are the constants determined by measurements of the FEA with units of A/V2 and V/m, respectively. EFN is the electric field that exists between the electron emissive tip and the positively biased structure drawing the electrons out. Typical constants for Spindt type cathodes include: AFN = 3.14 x 10-8 A/V2 and BFN = 771 V/m. (Stanford Research Institute data sheet). An accelerating structure is typically placed in close proximity with the emitting material as in the below figure.[44] Close (micrometer scale) proximity between the emitter and gate, combined with natural or artificial focusing structures, efficiently provide the high field strengths required for emission with relatively low applied voltage and power.
A carbon nanotube field-emission cathode was successfully tested on the KITE Electrodynamic tether experiment on the Japanese H-II Transfer Vehicle.[45]
Field emission cathodes are often in the form of Field Emitter Arrays (FEAs), such as the cathode design by Spindt et al. The figure below displays close up visual images of a Spindt emitter.[46][47][48]

A variety of materials have been developed for field emitter arrays, ranging from silicon to semiconductor fabricated molybdenum tips with integrated gates to a plate of randomly distributed carbon nanotubes with a separate gate structure suspended above.[44] The advantages of field emission technologies over alternative electron emission methods are:
- No requirement for a consumable (gas) and no resulting safety considerations for handling a pressurized vessel
- A low-power capability
- Having moderate power impacts due to space-charge limits in the emission of the electrons into the surrounding plasma.
One major issue to consider for field emitters is the effect of contamination. In order to achieve electron emission at low voltages, field emitter array tips are built on a micrometer-level scale sizes. Their performance depends on the precise construction of these small structures. They are also dependent on being constructed with a material possessing a low work-function. These factors can render the device extremely sensitive to contamination, especially from hydrocarbons and other large, easily polymerized molecules.[44] Techniques for avoiding, eliminating, or operating in the presence of contaminations in ground testing and ionospheric (e.g. spacecraft outgassing) environments are critical. Research at the University of Michigan and elsewhere has focused on this outgassing issue. Protective enclosures, electron cleaning, robust coatings, and other design features are being developed as potential solutions.[44] FEAs used for space applications still require the demonstration of long term stability, repeatability, and reliability of operation at gate potentials appropriate to the space applications.[49]
Hollow cathode
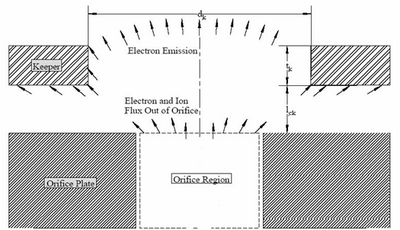
Hollow cathodes emit a dense cloud of plasma by first ionizing a gas. This creates a high density plasma plume which makes contact with the surrounding plasma. The region between the high density plume and the surrounding plasma is termed a double sheath or double layer. This double layer is essentially two adjacent layers of charge. The first layer is a positive layer at the edge of the high potential plasma (the contactor plasma cloud). The second layer is a negative layer at the edge of the low potential plasma (the ambient plasma). Further investigation of the double layer phenomenon has been conducted by several people.[50][51][52][53] One type of hollow cathode consists of a metal tube lined with a sintered barium oxide impregnated tungsten insert, capped at one end by a plate with a small orifice, as shown in the below figure.[54][55] Electrons are emitted from the barium oxide impregnated insert by thermionic emission. A noble gas flows into the insert region of the HC and is partially ionized by the emitted electrons that are accelerated by an electric field near the orifice (Xenon is a common gas used for HCs as it has a low specific ionization energy (ionization potential per unit mass). For EDT purposes, a lower mass would be more beneficial because the total system mass would be less. This gas is just used for charge exchange and not propulsion.). Many of the ionized xenon atoms are accelerated into the walls where their energy maintains the thermionic emission temperature. The ionized xenon also exits out of the orifice. Electrons are accelerated from the insert region, through the orifice to the keeper, which is always at a more positive bias.

In electron emission mode, the ambient plasma is positively biased with respect to the keeper. In the contactor plasma, the electron density is approximately equal to the ion density. The higher energy electrons stream through the slowly expanding ion cloud, while the lower energy electrons are trapped within the cloud by the keeper potential.[55] The high electron velocities lead to electron currents much greater than xenon ion currents. Below the electron emission saturation limit the contactor acts as a bipolar emissive probe. Each outgoing ion generated by an electron allows a number of electrons to be emitted. This number is approximately equal to the square root of the ratio of the ion mass to the electron mass.
It can be seen in the below chart what a typical I-V curve looks like for a hollow cathode in electron emission mode. Given a certain keeper geometry (the ring in the figure above that the electrons exit through), ion flow rate, and Vp, the I-V profile can be determined.[54][55][56] [111-113].

The operation of the HC in the electron collection mode is called the plasma contacting (or ignited) operating mode. The “ignited mode” is so termed because it indicates that multi-ampere current levels can be achieved by using the voltage drop at the plasma contactor. This accelerates space plasma electrons which ionize neutral expellant flow from the contactor. If electron collection currents are high and/or ambient electron densities are low, the sheath at which electron current collection is sustained simply expands or shrinks until the required current is collected.
In addition, the geometry affects the emission of the plasma from the HC as seen in the below figure. Here it can be seen that, depending on the diameter and thickness of the keeper and the distance of it with respect to the orifice, the total emission percentage can be affected.[57]
Plasma collection and emission summary
All of the electron emission and collection techniques can be summarized in the table following. For each method there is a description as to whether the electrons or ions in the system increased or decreased based on the potential of the spacecraft with respect to the plasma. Electrons (e-) and ions (ions+) indicates that the number of electrons or ions are being increased (↑) or reduced (↓). Also, for each method some special conditions apply (see the respective sections in this article for further clarification of when and where it applies).
Passive e− and ion emission/collection V − Vp < 0 V − Vp > 0 Bare tether: OML ions+ ↑ e− ↑ Ram collection ions+ ↑ 0 Thermal collection ions+ ↑ e− ↑ Photoemmision e− ↓ e− ↓,~0 Secondary electron emission e− ↓ e− ↓ Secondary ion emission ions+ ↓,~0 0 Retardation regieme e− ↑ ions+ ↑, ~0 Active e− and ion emission Potential does not matter Thermionic emission e− ↓ Field emitter arrays e− ↓ Hollow cathodes e− ↓ e− ↑
For use in EDT system modeling, each of the passive electron collection and emission theory models has been verified by reproducing previously published equations and results. These plots include: orbital motion limited theory,[15] Ram collection, and thermal collection,[58] photoemission,[59] secondary electron emission,[60] and secondary ion emission.[61][62][63][64]
Electrodynamic tether system fundamentals
In order to integrate all the most recent electron emitters, collectors, and theory into a single model, the EDT system must first be defined and derived. Once this is accomplished it will be possible to apply this theory toward determining optimizations of system attributes.
There are a number of derivations that solve for the potentials and currents involved in an EDT system numerically.[65][66][67][68] The derivation and numerical methodology of a full EDT system that includes a bare tether section, insulating conducting tether, electron (and ion) endbody emitters, and passive electron collection is described. This is followed by the simplified, all insulated tether model. Special EDT phenomena and verification of the EDT system model using experimental mission data will then be discussed.
Bare tether system derivation
An important note concerning an EDT derivation pertains to the celestial body which the tether system orbits. For practicality, Earth will be used as the body that is orbited; however, this theory applies to any celestial body with an ionosphere and a magnetic field.
The coordinates are the first thing that must be identified. For the purposes of this derivation, the x- and y-axis are defined as the east-west, and north-south directions with respect to the Earth's surface, respectively. The z-axis is defined as up-down from the Earth's center, as seen in the figure below. The parameters – magnetic field B, tether length L, and the orbital velocity vorb – are vectors that can be expressed in terms of this coordinate system, as in the following equations:
- (the magnetic field vector),
- (the tether position vector), and
- (the orbital velocity vector).
The components of the magnetic field can be obtained directly from the International Geomagnetic Reference Field (IGRF) model. This model is compiled from a collaborative effort between magnetic field modelers and the institutes involved in collecting and disseminating magnetic field data from satellites and from observatories and surveys around the world. For this derivation, it is assumed that the magnetic field lines are all the same angle throughout the length of the tether, and that the tether is rigid.
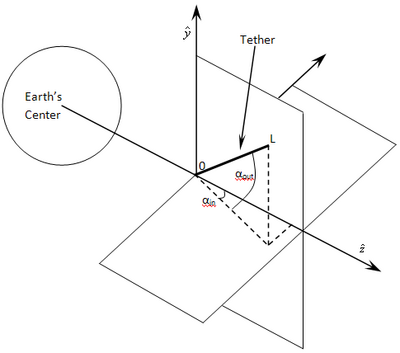
Realistically, the transverse electrodynamic forces cause the tether to bow and to swing away from the local vertical. Gravity gradient forces then produce a restoring force that pulls the tether back towards the local vertical; however, this results in a pendulum-like motion (Gravity gradient forces also result in pendulous motions without ED forces). The B direction changes as the tether orbits the Earth, and thus the direction and magnitude of the ED forces also change. This pendulum motion can develop into complex librations in both the in-plane and out-of-plane directions. Then, due to coupling between the in-plane motion and longitudinal elastic oscillations, as well as coupling between in-plane and out-of-plane motions, an electrodynamic tether operated at a constant current can continually add energy to the libration motions. This effect then has a chance to cause the libration amplitudes to grow and eventually cause wild oscillations, including one such as the 'skip-rope effect',[69] but that is beyond the scope of this derivation. In a non-rotating EDT system (A rotating system, called Momentum Exchange Electrodynamic Reboost [MXER]), the tether is predominantly in the z-direction due to the natural gravity gradient alignment with the Earth.
Derivations
The following derivation will describe the exact solution to the system accounting for all vector quantities involved, and then a second solution with the nominal condition where the magnetic field, the orbital velocity, and the tether orientation are all perpendicular to one another. The final solution of the nominal case is solved for in terms of just the electron density, n_e, the tether resistance per unit length, R_t, and the power of the high voltage power supply, P_hvps.
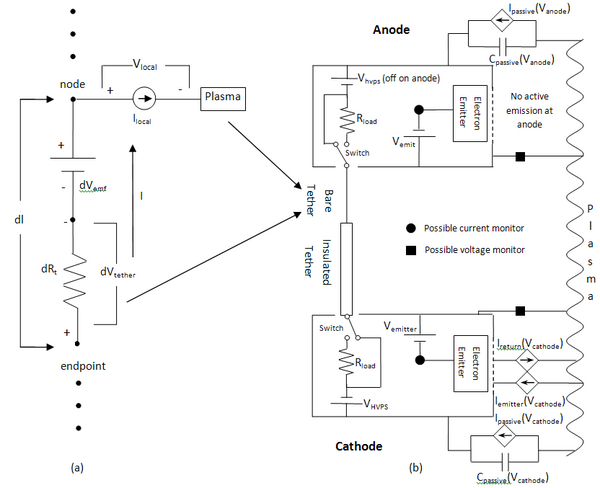
The below figure describes a typical EDT system in a series bias grounded gate configuration (further description of the various types of configurations analyzed have been presented[16]) with a blow-up of an infinitesimal section of bare tether. This figure is symmetrically set up so either end can be used as the anode. This tether system is symmetrical because rotating tether systems will need to use both ends as anodes and cathodes at some point in its rotation. The V_hvps will only be used in the cathode end of the EDT system, and is turned off otherwise.
In-plane and out-of-plane direction is determined by the orbital velocity vector of the system. An in-plane force is in the direction of travel. It will add or remove energy to the orbit, thereby increasing the altitude by changing the orbit into an elliptical one. An out-of-plane force is in the direction perpendicular to the plane of travel, which causes a change in inclination. This will be explained in the following section.
To calculate the in-plane and out-of-plane directions, the components of the velocity and magnetic field vectors must be obtained and the force values calculated. The component of the force in the direction of travel will serve to enhance the orbit raising capabilities, while the out-of-plane component of thrust will alter the inclination. In the below figure, the magnetic field vector is solely in the north (or y-axis) direction, and the resulting forces on an orbit, with some inclination, can be seen. An orbit with no inclination would have all the thrust in the in-plane direction.[70]
 |
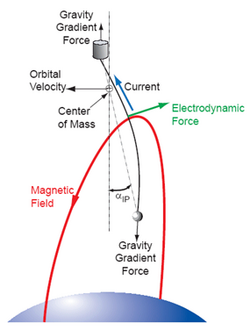 |
There has been work conducted to stabilize the librations of the tether system to prevent misalignment of the tether with the gravity gradient. The below figure displays the drag effects an EDT system will encounter for a typical orbit. The in-plane angle, α_ip, and out-of-plane angle, α_op, can be reduced by increasing the endmass of the system, or by employing feedback technology.[69] Any deviations in the gravity alignment must be understood, and accounted for in the system design.
Interstellar travel
An application of the EDT system has been considered and researched for interstellar travel by using the local interstellar medium of the Local Bubble. It has been found to be feasible to use the EDT system to supply on-board power given a crew of 50 with a requirement of 12 kilowatts per person. Energy generation is achieved at the expense of kinetic energy of the spacecraft. In reverse the EDT system could be used for acceleration. However, this has been found to be ineffective. Thrustless turning using the EDT system is possible to allow for course correction and rendezvous in interstellar space. It will not, however, allow rapid thrustless circling to allow a starship to re-enter a power beam or make numerous solar passes due to an extremely large turning radius of 3.7*1013 km (~3.7 lightyears).[71]
See also
- STARS-II
- HTV-6
- Tether propulsion
- Earth's magnetic field
- Tether satellite
- Atmospheric electricity
- STS-75
- Magnetic sail
- Electric sail
- Spacecraft propulsion
References
- General information
- Cosmo, M.L., and Lorenzini, E.C., "Tethers in Space Handbook," NASA Marchall Space Flight Center, 1997, pp. 274–1-274.
- Mariani, F., Candidi, M., Orsini, S., "Current Flow Through High-Voltage Sheaths Observer by the TEMAG Experiment During TSS-1R," Geophysical Research Letters, Vol. 25, No. 4, 1998, pp. 425–428.
- Citations
- ↑ 1.0 1.1 NASA, Tethers In Space Handbook, edited by M.L. Cosmo and E.C. Lorenzini, Third Edition December 1997 (accessed 20 October 2010); see also version at NASA MSFC; available on scribd
- ↑ Messier, Doug (12 March 2012). "Company Gets $1.9 Million from NASA to Develop Debris Removal Spacecraft". Parabolic Arc. http://www.parabolicarc.com/2012/03/12/company-gets-1-9-million-from-nasa-to-develop-debris-removal-spacecraft/.
- ↑ 3.0 3.1 Johnson & Herrmann (1998). "International Space Station Electrodynamic Tether Reboost Study ". https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19980223479.pdf.
- ↑ Fuhrhop, K.R., Gilchrist, B.E., Bilen, S.G., "System Analysis of the Expected Electrodynamic Tether Performance for the ProSEDS Mission," 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, AIAA, 2003, pp. 1–10.
- ↑ Johnson, L., Estes, R.D., Lorenzini, E.C., "Propulsive Small Expendable Deployer System Experiment," Journal of Spacecraft and Rockets, Vol. 37, No. 2, 2000, pp. 173–176.
- ↑ Lorenzini, E.C., Welzyn, K., and Cosmo, M.L., "Expected Deployment Dynamics of ProSEDS," 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, AIAA, 2003, pp. 1–9.
- ↑ Sanmartin, J.R., Charro, M., Lorenzini, E.C., "Analysis of ProSEDS Test of Bare-tether Collection," 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, AIAA, 2003, pp. 1–7.
- ↑ Vaughn, J.A., Curtis, L., Gilchrist, B.E., "Review of the ProSEDS Electrodynamic Tether Mission Development," 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, AIAA, 2004, pp. 1–12.
- ↑ 9.0 9.1 Sanmartin, J.R., Martinez-Sanchez, M., and Ahedo, E., "Bare Wire Anodes for Electrodynamic Tethers," Journal of Propulsion and Power, Vol. 9, No. 3, 1993, pp. 353–360
- ↑ Tether power generator for earth orbiting satellites. Thomas G. Roberts et al.
- ↑ Katz, I.; Lilley, J. R. Jr.; Greb, A. (1995). "Plasma Turbulence Enhanced Current Collection: Results from the Plasma Motor Generator Electrodynamic Tether Flight". J. Geophys. Res. 100 (A2): 1687–90. doi:10.1029/94JA03142. Bibcode: 1995JGR...100.1687K.
- ↑ US Standard Patent 6116544, Forward & Hoyt, Electrodynamic tether and method of use, 1986
- ↑ 13.0 13.1 Lieberman, M.A., and Lichtenberg, A.J., "Principles of Plasma Discharges and Materials Processing," Wiley-Interscience, Hoboken, NJ, 2005, pp. 757.
- ↑ Mott-Smith, H.M., and Langmuir, I., "The Theory of Collectors in Gaseous Discharges," Physical Review, Vol. 28, 1926, pp. 727–763.
- ↑ 15.0 15.1 15.2 15.3 Choinere, E., "Theory and Experimental Evaluation of a Consistent Steady State Kinetic Model for 2-D Conductive Structures in Ionospheric Plasmas with Application to Bare Electrodynamic Tethers in Space," 2004, pp. 1–313.
- ↑ 16.0 16.1 16.2 Fuhrhop, K.R.P., “ Theory and Experimental Evaluation of Electrodynamic Tether Systems and Related Technologies,”University of Michigan PhD Dissertation, 2007, pp. 1-307. "Theory and Experimental Evaluation of Electrodynamic Tether Systems and Related Technologies". http://data.engin.umich.edu/sets/papers/Fuhrhop_thesis_2007.pdf.
- ↑ Rosen, G. (1962). "Method for removal of free electrons in a plasma". Phys. Fluids 5 (6): 737. doi:10.1063/1.1706691. Bibcode: 1962PhFl....5..737R.
- ↑ email from Robert Merlino to Gerald Rosen, Jan 22, 2010
- ↑ Sanmartin, J.R., and Estes, R.D., "The orbital-motion-limited regime of cylindrical Langmuir probes," Physics of Plasmas, Vol. 6, No. 1, 1999, pp. 395–405.
- ↑ Choiniere, E., Gilchrist, B.E., Bilen, S.G., "Measurement of Cross-Section GeometryEffects on Electron Collection to Long Probes in Mesosonic Flowing Plasmas," 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, AIAA, 2003, pp. 1–13.
- ↑ Choiniere, E., and Gilchrist, B.G., "Investigation of Ionospheric Plasma Flow Effects on Current Collection to Parallel Wires Using Self-Consistent Steady-State Kinetic Simulations," 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, AIAA, 2005, pp. 1–13.
- ↑ Parker, L.W., "Plasmasheath-Photosheath theory for Large High-Voltage Space Structures," edited by H.B. Garrett and C.P. Pike, Space Systems and their Interactions with the Earth's Space Environment, AIAA Press, 1980, pp. 477–491.
- ↑ Gombosi, T.I., "Physics of Space Environments," Dessler, A.J. Houghton, J.T. and Rycroft, M.J. eds., Cambridge University Press, Cambridge, UK, 1998, pp. 1–339.
- ↑ Stone, N.H., and Bonifazi, C., "The TSS-1R mission: Overview and Scientific Context," Geophysical Research Letters, Vol. 25, No. 4, 1998, pp. 409–412.
- ↑ Gregory, F. D., "NASA Safety Standard Guidelines and Assessment Procedures for Limiting Orbital Debris," NASA, NSS 1740.14, Washington D.C., 1995
- ↑ Bilitza, D., "International Reference Ionosphere 2000," Radio Science, Vol. 36, No. 2, 2001, pp. 261–275.
- ↑ Bilitza, D., "International Reference Ionosphere – Status 1995/96," Advanced Space Research, Vol. 20, No. 9, 1997, pp. 1751–1754.
- ↑ Wertz, J.R., and Larson, W.J. eds., "Space Mission Analysis and Design," Microcosm Press & Kluwar Academic Publishers, El Segundo, CA, 1999, pp. 1–985.
- ↑ Stone, N.H., and Gierow, P.A., "A Preliminary Assessment of Passive End-Body Plasma Contactors," 39th Aerospace Sciences Meeting and Exhibit, AIAA, 2001, pp. 1–6.
- ↑ Stone, N.H., and Moore, J.D., "Grid Sphere Electrodes used for Current Collection at the Positive Pole of Electrodynamic Tethers," 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, AIAA, 2004, pp. 1–7.
- ↑ 31.0 31.1 Khazanov, G.V., Krivorutsky, E., and Sheldon, R.B., "Solid and grid sphere current collectionin view of the tethered satellite systemTSS 1 and TSS 1R mission results," Journal of Goephysical Research, Vol. 110, 2005, pp. 1–10.
- ↑ Child, C.D., "Discharge From Hot CaO," Physical Review (Series I), Vol. 32, No. 5, 1911, pp. 492–511.
- ↑ Langmuir, I., "The Effect of Space Charge and Initial Velocities on the Potential Distribution and Thermionic Current between Parallel Plane Electrodes," Physical Review, Vol. 21, No. 4, 1923, pp. 419–435
- ↑ Langmuir, I., "The Effect of Space Charge and Residual Gases on Thermionic Currents in High Vacuum," Physical Review, Vol. 2, No. 6, 1913, pp. 450–486.
- ↑ Luginsland, J.W., McGee, S., and Lau, Y.Y., "Virtual Cathode Formation Due to Electromagnetic Transients," IEEE Transactions on Plasma Science, Vol. 26, No. 3, 1998, pp. 901–904.
- ↑ Lau, Y.Y., "Simple Theory for the Two-Dimensional Child-Langmuir Law," Physical Review Letters, Vol. 87, No. 27, 2001, pp. 278301/1-278301/3.
- ↑ Luginsland, J.W., Lau, Y.Y., and Gilgenbach, R.M., "Two-Dimensional Child-Langmuir Law," Physical Review Letters, Vol. 77, No. 22, 1996, pp. 4668–4670.
- ↑ Humphries, S.J., "Charged Particle Beams," John Wiley & Sons, Inc., New York, 1990, pp. 834.
- ↑ Dekker, A.J., "Thermionic Emission," McGraw Hill Access Science Encyclopedia, Vol. 2004, No. 5 / 3, 2002, pp. 2.
- ↑ 40.0 40.1 Dobrowolny, M., and Stone, N.H., "A Technical Overview of TSS-1: the First Tethered-Satellite System Mission," Il Nuovo Cimento Della Societa Italiana Di Fisica, Vol. 17C, No. 1, 1994, pp. 1–12.
- ↑ Bonifazi, C., Svelto, F., and Sabbagh, J., "TSS Core Equipment I – Electrodynamic Package and Rational for System Electrodynamic Analysis," Il Nuovo Cimento Della Societa Italiana Di Fisica, Vol. 17C, No. 1, 1994, pp. 13–47.
- ↑ Gunther, K., "Hollow Cathode / Ion Source Quotation," HeatWave Labs, Inc., 3968, Watsonville, CA, 2006.
- ↑ 43.0 43.1 Gomer, R., "Field emission," McGraw Hill Access Science Encyclopedia, Vol. 2005, No. July 1, 2002, pp. 2.
- ↑ 44.0 44.1 44.2 44.3 Morris, D., "Optimizing Space-Charge Limits of Electron Emission into Plasmas in Space Electric Propulsion," University of Michigan, 2005, pp. 1–212.
- ↑ Ohkawa, Y., (December 2020). "Review of KITE - Electrodynamic tether experiment on the Japanese H-II Transfer Vehicle", Acta Astronautica, Vol. 177, pp. 750-758. https://doi.org/10.1016/j.actaastro.2020.03.014 Retrieved 16 July 2021.
- ↑ Spindt, C.A., Holland, C.E., and Rosengreen, A. Brodie, I., "Field-Emitter Arrays for Vacuum Microelectronics," IEEE Transactions on Electron Devices, Vol. 38, No. 10, 1991, pp. 2355–2363.
- ↑ Spindt, C.A., "Spindt Emitter Measurements," unpublished material Stanford Research Institute, 2001, pp. 1.
- ↑ Jensen, K.L., "Field emitter arrays for plasma and microwave source applications," Physics of Plasmas, Vol. 6, No. 5, 1999, pp. 2241–2253.
- ↑ Gilchrist, B.E., Gallimore, A.D., Jensen, K.L., "Field-Emitter Array Cathodes (FEACs) for Space-Based Applications: An Enabling Technology," Not Published, University of Michigan, 2001.
- ↑ Lapuerta, V., and Ahedo, E., " Dynamic model of a plasma structure with an intermediate double-layer, formed outside an anodic plasma contactor," Physics of Plasmas, Vol. 7, No. 6, 2000, pp. 2693–2703.
- ↑ Wells, A.A., "Current Flow Across a Plasma Double Layer in a Hollow Cathode Ion Thruster," AIAA 9th Electric Propulsion Conference, AIAA, 1972, pp. 1–15.
- ↑ Andrews, J.G., and Allen, J.E., "Theory of a Double Sheath Between Two Plasmas," Proceedings of the Royal Society of London Series A, Vol. 320, No. 1543, 1971, pp. 459–472.
- ↑ Prewett, P.D., and Allen, J.E., "The double sheath Associated with a Hot Cathode," Proceedings of the Royal Society of London Series A, Vol. 348, No. 1655, 1976, pp. 435–446.
- ↑ 54.0 54.1 54.2 Katz, I., Anderson, J.R., Polk, J.E., "One-Dimensional Hollow Cathode Model," Journal of Propulsion and Power, Vol. 19, No. 4, 2003, pp. 595–600.
- ↑ 55.0 55.1 55.2 Katz, I., Lilley, J. R. Jr., Greb, A., "Plasma Turbulence Enhanced Current Collection: Results from the Plasma Motor Generator Electrodynamic Tether Flight," Journal of Geophysical Research, Vol. 100, No. A2, 1995, pp. 1687–1690.
- ↑ 56.0 56.1 Parks, D.E., Katz, I., Buchholtz, B., "Expansion and electron emission characteristics of a hollow-cathode plasma contactor," Journal of Applied Physics, Vol. 74, No. 12, 2003, pp. 7094–7100.
- ↑ 57.0 57.1 Domonkos, M.T., "Evaluation of Low-Current Orificed Hollow Cathodes," University of Michigan PhD Dissertation, 1999, pp. 1–173.
- ↑ Aguero, V.M., "A Study of Electrical Charging on Large LEO Spacecraft Using a Tethered Satellite as a Remote Plasma Reference," Stanford University, Space, Telecommunications and Radioscience Laboratory, 1996, pp. 1–192
- ↑ Whipple, E.C., "Potentials of Surfaces in Space," Report of Progress in Physics, Vol. 44, 1981, pp. 1197–1250.
- ↑ Hastings, D., and Garrett, H., "Spacecraft – Environment Interactions," Cambridge University Press, New York, NY, 1996, pp. 292.
- ↑ Siegel, M.W., and Vasile, M.J., "New wide angle, high transmission energy analyzer for secondary ion mass spectrometry," Review of Scientific Instrumentation, Vol. 52, No. 11, 1981, pp. 1603–1615.
- ↑ Benninghoven, A., "Developments in Secondary-Ion Mass Spectroscopy and Applications to Surface Studies," Surface Science, Vol. 53, 1975, pp. 596–625
- ↑ Benninghoven, A., "Surface Investigation of Solids by the Statistical Method of Secondary-Ion Mass Spectroscopy (SIMS)," Surface Science, Vol. 35, 1973, pp. 427–457.
- ↑ Benninghoven, A., and Mueller, A., "Secondary ion yields near 1 for some chemical compounds," Physics Letters, Vol. 40A, No. 2, 1972, pp. 169–170.
- ↑ Dobrowolny, M., "Electrodynamics of Long Metal Tethers in the Ionospheric Plasma," Radio Science, Vol. 13, No. 3, 1978, pp. 417–424.
- ↑ Arnold, D.A., and Dobrowolny, M., "Transmission Line Model of the Interaction of a Long Metal Wire with the Ionosphere," Radio Science, Vol. 15, No. 6, 1980, pp. 1149–1161.
- ↑ Dobrowolny, M., Vannaroni, G., and DeVenuto, F., "Electrodynamic Deorbiting of LEO satellites," Nuovo Cimento, Vol. 23C, No. 1, 2000, pp. 1–21.
- ↑ Dobrowolny, M., Colombo, G., and Grossi, M.D., "Electrodynamics of long conducting tethers in the near-earth environment," Interim Report Smithsonian Astrophysical Observatory, 1976, pp. 1–48.
- ↑ 69.0 69.1 69.2 Hoyt, R.P., "Stabilization of Electrodynamic Tethers," 38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, 2002, pp. 1–9.
- ↑ Bonometti, J.A., Sorensen, K.F., Jansen, R.H., "Free Re-boost Electrodynamic Tether on the International Space Station," 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, AIAA, 2005, pp. 1–7.
- ↑ "Applications of the Electrodynamic Tether to Interstellar Travel" Gregory L. Matloff, Less Johnson, February, 2005
Further reading
- Dobrowolny, M. (1979). Wave and particle phenomena induced by an electrodynamic tether. SAO special report, 388. Cambridge, Mass: Smithsonian Institution Astrophysical Observatory.
- Williamson, P. R. (1986). High voltage characteristics of the electrodynamic tether and the generation of power and propulsion final report. [NASA contractor report], NASA CR-178949. Washington, DC: National Aeronautics and Space Administration.
External links
- Related patents
- U.S. Patent 3,174,705, "Space station and system for operating same".
- U.S. Patent 3,205,381, "Ionospheric battery".
- U.S. Patent 4,097,010, "Satellite connected by means of a long tether to a powered spacecraft ".
- U.S. Patent 6,116,544, "Electrodynamic Tether And Method of Use".
- Publications
- Samanta Roy, R.I.; Hastings, D.E.; Ahedo, E. (1992). "Systems analysis of electrodynamic tethers". J Spacecr Rockets 29 (3): 415–424. doi:10.2514/3.26366. Bibcode: 1992JSpRo..29..415S.
- Ahedo, E.; Sanmartin, J.R. (March–April 2002). "Analysis of bare-tethers systems for deorbiting Low-Earth-Orbit satellites". J Spacecr Rockets 39 (2): 198–205. doi:10.2514/2.3820. Bibcode: 2002JSpRo..39..198A.
- Peláez, J.; Sánchez-Arriaga, G.; Sanjurjo-Rivo, M. (October 2012). "Self balanced electrodynamic tethers for space debris mitigatation". 57th International Astronautical Conference. Valencia, Spain: AIAA. doi:10.2514/6.IAC-06-B6.4.03. ISBN 978-1-62410-042-0. https://arc.aiaa.org/doi/abs/10.2514/6.IAC-06-B6.4.03. Retrieved November 6, 2022.
- Cosmo, M. L., and E. C. Lorenzini, "Tethers in Space Handbook" (3rd ed). Prepared for NASA/MSFC by Smithsonian Astrophysical Observatory, Cambridge, MA, December 1997. (PDF)
- "New High-Current Tethers: A Viable Power Source for the Space Station? A White Paper". December 1995. http://cfa-www.harvard.edu/~spgroup/SAO_White_Paper.pdf.
- Savich, N.A.; Sanmartín, J.R. (1994). "Short, High Current Electrodynamic Tether". p. 417.
- McCoy, James E. (April 1995). "Plasma Motor-Generator (PMG) Flight Experiment Results". Washington DC. pp. 57–84.
- Other articles
- "Electrodynamic Tethers ". Tethers.com.
- "Shuttle Electrodynamic Tether System (SETS)".
- Enrico Lorenzini and Juan Sanmartín, "Electrodynamic Tethers in Space; By exploiting fundamental physical laws, tethers may provide low-cost electrical power, drag, thrust, and artificial gravity for spaceflight". Scientific American, August 2004.
- "Tethers". Astronomy Study Guide, BookRags.
- David P. Stern, "The Space Tether Experiment". 25 November 2001.
 |
 KSF
KSF