Front

In physics, a front^[1][2] can be understood as an interface between two different possible states (either stable or unstable) in a physical system. For example, a weather front is the interface between two different density masses of air, in combustion where the flame is the interface between burned and unburned material or in population dynamics where the front is the interface between populated and unpopulated places. Fronts can be static or mobile depending on the conditions of the system, and the causes of the motion can be the variation of a free energy, where the most energetically favorable state invades the less favorable one, according to Pomeau^[3] or shape induced motion due to non-variation dynamics in the system, according to Alvarez-Socorro, Clerc, González-Cortés and Wilson.^[4] From a mathematical point of view, fronts are solutions of spatially extended systems connecting two steady states, and from dynamical systems point of view, a front corresponds to a heteroclinic orbit of the system in the co-mobile frame (or proper frame).

The motion of magnetization domains front. Black state (a magnetization direction in the material) invades the white state (opposite magnetization direction). The fronts are the interfaces between black and white areas.

Fronts connecting stable - unstable homogeneous states

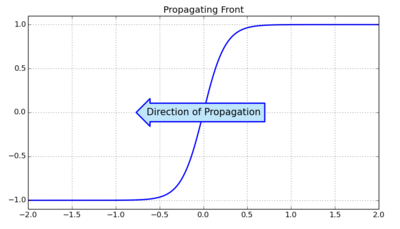
The most simple example of front solution connecting a homogeneous stable state with a homogeneous unstable state can be shown in the one-dimensional Fisher–Kolmogorov equation:

[math]\displaystyle{ N_{t} = D N_{xx} + r N (N_0-N) }[/math]

that describes a simple model for the density [math]\displaystyle{ N(x,t) }[/math] of population. This equation has two steady states, [math]\displaystyle{ N = 0 }[/math], and [math]\displaystyle{ N = N_0 }[/math]. This solution corresponds to extinction and saturation of population. Observe that this model is spatially-extended, because it includes a diffusion term given by the second derivative. The state [math]\displaystyle{ N \equiv N_0 }[/math] is stable as a simple linear analysis can show and the state [math]\displaystyle{ N = 0 }[/math] is unstable. There exist a family of front solutions connecting [math]\displaystyle{ N=N_0 }[/math] with [math]\displaystyle{ N=0 }[/math], and such solution are propagative. Particularly, there exist one solution of the form [math]\displaystyle{ N(t,x)=N(x-vt) }[/math], with [math]\displaystyle{ v }[/math] is a velocity that only depends on [math]\displaystyle{ D }[/math] and [math]\displaystyle{ r }[/math]^[5]

Front solution connecting two steady states in a generic spatially extended system.

Propagative front profile

References

0.00 (0 votes)