Goldschmidt tolerance factor
Topic: Physics
 From HandWiki - Reading time: 2 min
From HandWiki - Reading time: 2 min
Goldschmidt's tolerance factor (from the German word Toleranzfaktor) is an indicator for the stability and distortion of crystal structures.[1] It was originally only used to describe the perovskite ABO3 structure, but now tolerance factors are also used for ilmenite.[2]
Alternatively the tolerance factor can be used to calculate the compatibility of an ion with a crystal structure.[3]
The first description of the tolerance factor for perovskite was made by Victor Moritz Goldschmidt in 1926.[4]
Mathematical expression
The Goldschmidt tolerance factor ([math]\displaystyle{ t }[/math]) is a dimensionless number that is calculated from the ratio of the ionic radii:[1]
| [math]\displaystyle{ t={r_A+r_O \over \sqrt{2}(r_B+r_O)} }[/math] | ||
| rA is the radius of the A cation. | rB is the radius of the B cation. | rO is the radius of the anion (usually oxygen). |
In an ideal cubic perovskite structure, the lattice parameter (i.e., length) of the unit cell (a) can be calculated using the following equation:[1]
| [math]\displaystyle{ a=\sqrt{2}(r_A+r_O)=2(r_B+r_O) }[/math] | ||
| rA is the radius of the A cation. | rB is the radius of the B cation. | rO is the radius of the anion (usually oxygen). |
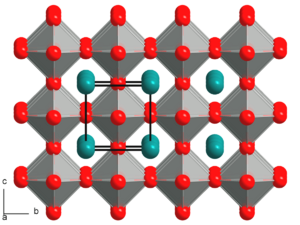
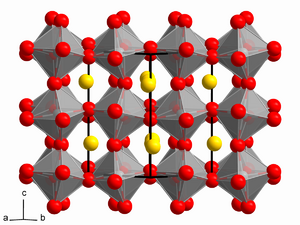
Perovskite structure
The perovskite structure has the following tolerance factors (t):
| Goldschmidt tolerance factor (t) | Structure | Explanation | Example | Example lattice |
|---|---|---|---|---|
| >1[3] | Hexagonal or Tetragonal | A ion too big or B ion too small. |
|
- |
| 0.9-1[3] | Cubic | A and B ions have ideal size. |
|
|
| 0.71 - 0.9[3] | Orthorhombic/Rhombohedral | A ions too small to fit into B ion interstices. | ||
| <0.71[3] | Different structures | A ions and B have similar ionic radii. | - |
See also
- Goldschmidt classification
- Victor Goldschmidt
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 Parkin, ((editors-in-chief, Helmut Kronmller, Stuart)); Mats Johnsson; Peter Lemmens (2007). Handbook of magnetism and advanced magnetic materials ([Online-Ausg.] ed.). Hoboken, NJ: John Wiley & Sons. ISBN 978-0-470-02217-7. https://books.google.com/books?id=N-rXAAAAMAAJ&q=Handbook+of+magnetism+and+advanced+magnetic+materials. Retrieved 17 May 2012.
- ↑ Liu, XiangChun; Hong, Rongzi; Tian, Changsheng (24 April 2008). "Tolerance factor and the stability discussion of ABO3-type ilmenite". Journal of Materials Science: Materials in Electronics 20 (4): 323–327. doi:10.1007/s10854-008-9728-8.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 Schinzer, Carsten. "Distortion of Perovskites". http://www.ccp14.ac.uk/ccp/web-mirrors/pki/uni/pki/members/schinzer/stru_chem/perov/di_gold.html. Retrieved 17 May 2012.
- ↑ Goldschmidt, Victor M. (1926). "Die Gesetze der Krystallochemie". Die Naturwissenschaften 14 (21): 477–485. doi:10.1007/bf01507527. Bibcode: 1926NW.....14..477G.
 |
 KSF
KSF