Hamiltonian constraint
Topic: Physics
 From HandWiki - Reading time: 12 min
From HandWiki - Reading time: 12 min
The Hamiltonian constraint arises from any theory that admits a Hamiltonian formulation and is reparametrisation-invariant. The Hamiltonian constraint of general relativity is an important non-trivial example.
In the context of general relativity, the Hamiltonian constraint technically refers to a linear combination of spatial and time diffeomorphism constraints reflecting the reparametrizability of the theory under both spatial as well as time coordinates. However, most of the time the term Hamiltonian constraint is reserved for the constraint that generates time diffeomorphisms.
Simplest example: the parametrized clock and pendulum system
Parametrization
In its usual presentation, classical mechanics appears to give time a special role as an independent variable. This is unnecessary, however. Mechanics can be formulated to treat the time variable on the same footing as the other variables in an extended phase space, by parameterizing the temporal variable(s) in terms of a common, albeit unspecified parameter variable. Phase space variables being on the same footing.
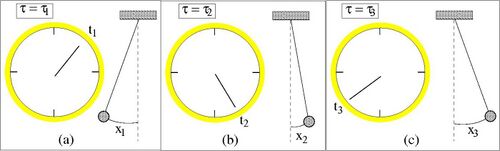
Say our system comprised a pendulum executing a simple harmonic motion and a clock. Whereas the system could be described classically by a position x=x(t), with x defined as a function of time, it is also possible to describe the same system as x([math]\displaystyle{ \tau }[/math]) and t([math]\displaystyle{ \tau }[/math]) where the relation between x and t is not directly specified. Instead, x and t are determined by the parameter [math]\displaystyle{ \tau }[/math], which is simply a parameter of the system, possibly having no objective meaning in its own right.
The system would be described by the position of a pendulum from the center, denoted [math]\displaystyle{ x }[/math], and the reading on the clock, denoted [math]\displaystyle{ t }[/math]. We put these variables on the same footing by introducing a fictitious parameter [math]\displaystyle{ \tau }[/math], [math]\displaystyle{ x (\tau), \;\;\;\; t (\tau) }[/math] whose 'evolution' with respect to [math]\displaystyle{ \tau }[/math] takes us continuously through every possible correlation between the displacement and reading on the clock. Obviously the variable [math]\displaystyle{ \tau }[/math] can be replaced by any monotonic function, [math]\displaystyle{ \tau' = f(\tau) }[/math]. This is what makes the system reparametrisation-invariant. Note that by this reparametrisation-invariance the theory cannot predict the value of [math]\displaystyle{ x (\tau) }[/math] or [math]\displaystyle{ t (\tau) }[/math] for a given value of [math]\displaystyle{ \tau }[/math] but only the relationship between these quantities. Dynamics is then determined by this relationship.
Dynamics of this reparametrization-invariant system
The action for the parametrized Harmonic oscillator is then [math]\displaystyle{ S = \int d \tau \left[ {dx \over d \tau} p + {dt \over d \tau} p_t - \lambda \left( p_t + {p^2 \over 2m} + {1 \over 2} m \omega^2 x^2 \right) \right], }[/math] where [math]\displaystyle{ x }[/math] and [math]\displaystyle{ t }[/math] are canonical coordinates and [math]\displaystyle{ p }[/math] and [math]\displaystyle{ p_t }[/math] are their conjugate momenta respectively and represent our extended phase space (we will show that we can recover the usual Newton's equations from this expression). Writing the action as [math]\displaystyle{ S = \int d \tau \left[ {dx \over d \tau} p + {dt \over d \tau} p_t - \mathcal{H} (x,t;p,p_t) \right] }[/math] we identify the [math]\displaystyle{ \mathcal{H} }[/math] as [math]\displaystyle{ \mathcal{H} (x,t,\lambda;p,p_t) = \lambda \left( p_t + {p^2 \over 2m} + {1 \over 2} m \omega^2 x^2 \right). }[/math]
Hamilton's equations for [math]\displaystyle{ \lambda }[/math] are [math]\displaystyle{ {\partial \mathcal{H} \over \partial \lambda} = 0 }[/math] which gives a constraint, [math]\displaystyle{ C = p_t + {p^2 \over 2m} + {1 \over 2} m \omega^2 x^2 = 0. }[/math]
[math]\displaystyle{ C }[/math] is our Hamiltonian constraint! It could also be obtained from the Euler–Lagrange equation of motion, noting that the action depends on [math]\displaystyle{ \lambda }[/math] but not its [math]\displaystyle{ \tau }[/math] derivative. Then the extended phase space variables [math]\displaystyle{ x }[/math], [math]\displaystyle{ t }[/math], [math]\displaystyle{ p }[/math], and [math]\displaystyle{ p_t }[/math] are constrained to take values on this constraint-hypersurface of the extended phase space. We refer to [math]\displaystyle{ \lambda C }[/math] as the `smeared' Hamiltonian constraint where [math]\displaystyle{ \lambda }[/math] is an arbitrary number. The 'smeared' Hamiltonian constraint tells us how an extended phase space variable (or function thereof) evolves with respect to [math]\displaystyle{ \tau }[/math]: [math]\displaystyle{ {dx \over d \tau} = \{ x , \lambda C \} , \;\;\;\; {dp \over d \tau} = \{ p , \lambda C \} \;\;\;\;\;\; {dt \over d \tau} = \{ t , \lambda C \}, \;\;\;\; {dp_t \over d \tau} = \{ p_t , \lambda C \} }[/math] (these are actually the other Hamilton's equations). These equations describe a flow or orbit in phase space. In general we have [math]\displaystyle{ {d F (x,p,t,p_t) \over d \tau} = \{ F (x,p,t,p_t) , \lambda C \} }[/math] for any phase space function [math]\displaystyle{ F }[/math]. As the Hamiltonian constraint Poisson commutes with itself, it preserves itself and hence the constraint-hypersurface. The possible correlations between measurable quantities like [math]\displaystyle{ x (\tau) }[/math] and [math]\displaystyle{ t (\tau) }[/math] then correspond to `orbits' generated by the constraint within the constraint surface, each particular orbit differentiated from each other by say also measuring the value of say [math]\displaystyle{ p (\tau) }[/math] along with [math]\displaystyle{ x (\tau) }[/math] and [math]\displaystyle{ t (\tau) }[/math] at one [math]\displaystyle{ \tau }[/math]-instant; after determining the particular orbit, for each measurement of [math]\displaystyle{ t (\tau) }[/math] we can predict the value [math]\displaystyle{ x (\tau) }[/math] will take.
Deparametrization
The other equations of Hamiltonian mechanics are [math]\displaystyle{ {dx \over d \tau} = {\partial \mathcal{H} \over \partial p}, \;\;\;\; {dp \over d \tau} = - {\partial \mathcal{H} \over \partial x} ; \;\;\;\;\;\; {dt \over d \tau} = {\partial \mathcal{H} \over \partial p_t}, \;\;\;\; {dp_t \over d \tau} = {\partial \mathcal{H} \over \partial t}. }[/math]
Upon substitution of our action these give, [math]\displaystyle{ {dx \over d \tau} = \lambda {p \over m}, \;\;\;\; {dp \over d \tau} = - \lambda m \omega^2 x ; \;\;\;\;\;\; {dt \over d \tau} = \lambda, \;\;\;\; {dp_t \over d \tau} = 0, }[/math]
These represent the fundamental equations governing our system.
In the case of the parametrized clock and pendulum system we can of course recover the usual equations of motion in which [math]\displaystyle{ t }[/math] is the independent variable:
Now [math]\displaystyle{ dx / dt }[/math] and [math]\displaystyle{ dp / dt }[/math] can be deduced by
[math]\displaystyle{ {dx \over dt} = {dx \over d \tau} \Big/ {dt \over d \tau} = {\lambda p/m \over \lambda} = {p \over m} }[/math] [math]\displaystyle{ {dp \over dt} = {dp \over d \tau} \Big/ {dt \over d \tau} = {- \lambda m \omega^2 x \over \lambda}= - m \omega^2 x. }[/math]
We recover the usual differential equation for the simple harmonic oscillator, [math]\displaystyle{ {d^2 x \over dt^2} = - \omega^2 x. }[/math]
We also have [math]\displaystyle{ dp_t / d t = dp_t / d \tau \big/ d t / d \tau = 0 }[/math] or [math]\displaystyle{ p_t = \mathrm{const}. }[/math]
Our Hamiltonian constraint is then easily seen as the condition of constancy of energy! Deparametrization and the identification of a time variable with respect to which everything evolves is the opposite process of parametrization. It turns out in general that not all reparametrisation-invariant systems can be deparametrized. General relativity being a prime physical example (here the spacetime coordinates correspond to the unphysical [math]\displaystyle{ \tau }[/math] and the Hamiltonian is a linear combination of constraints which generate spatial and time diffeomorphisms).
Reason why we could deparametrize here
The underlining reason why we could deparametrize (aside from the fact that we already know it was an artificial reparametrization in the first place) is the mathematical form of the constraint, namely, [math]\displaystyle{ C = p_t + C' (x,p). }[/math]
Substitute the Hamiltonian constraint into the original action we obtain [math]\displaystyle{ \begin{align} S &= \int d \tau \left[ {dx \over d \tau} p + {dt \over d \tau} p_t - \lambda (p_t + C' (x,p)) \right] \\ &= \int d \tau \left[ {dx \over d \tau} p - {dt \over d \tau} C' (x,p) \right] \\ &= \int dt \left[ {dx \over dt} p - {p^2 \over 2m} + {1 \over 2} m \omega^2 x^2 \right] \end{align} }[/math] which is the standard action for the harmonic oscillator. General relativity is an example of a physical theory where the Hamiltonian constraint isn't of the above mathematical form in general, and so cannot be deparametrized in general.
Hamiltonian of classical general relativity
In the ADM formulation of general relativity one splits spacetime into spatial slices and time, the basic variables are taken to be the induced metric, [math]\displaystyle{ q_{ab} (x) }[/math], on the spatial slice (the metric induced on the spatial slice by the spacetime metric), and its conjugate momentum variable related to the extrinsic curvature, [math]\displaystyle{ K^{ab} (x) }[/math], (this tells us how the spatial slice curves with respect to spacetime and is a measure of how the induced metric evolves in time).[1] These are the metric canonical coordinates.
Dynamics such as time-evolutions of fields are controlled by the Hamiltonian constraint.
The identity of the Hamiltonian constraint is a major open question in quantum gravity, as is extracting of physical observables from any such specific constraint.
In 1986 Abhay Ashtekar introduced a new set of canonical variables, Ashtekar variables to represent an unusual way of rewriting the metric canonical variables on the three-dimensional spatial slices in terms of a SU(2) gauge field and its complementary variable.[2] The Hamiltonian was much simplified in this reformulation. This led to the loop representation of quantum general relativity and in turn loop quantum gravity.[3]
Within the loop quantum gravity representation Thiemann formulated a mathematically rigorous operator as a proposal as such a constraint.[4] Although this operator defines a complete and consistent quantum theory, doubts have been raised[by whom?] as to the physical reality of this theory due to inconsistencies with classical general relativity (the quantum constraint algebra closes, but it is not isomorphic to the classical constraint algebra of GR, which is seen as circumstantial evidence of inconsistencies definitely not a proof of inconsistencies), and so variants have been proposed.
Metric formulation
The idea was to quantize the canonical variables [math]\displaystyle{ q_{ab} }[/math] and [math]\displaystyle{ \pi^{ab} = \sqrt{q} (K^{ab} - q^{ab} K_c^c) }[/math], making them into operators acting on wavefunctions on the space of 3-metrics, and then to quantize the Hamiltonian (and other constraints). However, this program soon became regarded as dauntingly difficult for various reasons, one being the non-polynomial nature of the Hamiltonian constraint: [math]\displaystyle{ H = \sqrt{\det (q)} (K_{ab} K^{ab} - (K_a^a)^2 -{}^3R) }[/math] where [math]\displaystyle{ \;^3R }[/math] is the scalar curvature of the three metric [math]\displaystyle{ q_{ab} (x) }[/math]. Being a non-polynomial expression in the canonical variables and their derivatives it is very difficult to promote to a quantum operator.
Expression using Ashtekar variables
The configuration variables of Ashtekar's variables behave like an [math]\displaystyle{ SU(2) }[/math] gauge field or connection [math]\displaystyle{ A_a^i }[/math]. Its canonically conjugate momentum is [math]\displaystyle{ \tilde{E}_i^a }[/math] is the densitized "electric" field or triad (densitized as [math]\displaystyle{ \tilde{E}_i^a = \sqrt{\det (q)} E_i^a }[/math]). What do these variables have to do with gravity? The densitized triads can be used to reconstruct the spatial metric via
[math]\displaystyle{ \det (q) q^{ab} = \tilde{E}_i^a \tilde{E}_j^b \delta^{ij}. }[/math]
The densitized triads are not unique, and in fact one can perform a local in space rotation with respect to the internal indices [math]\displaystyle{ i }[/math]. This is actually the origin of the [math]\displaystyle{ SU(2) }[/math] gauge invariance. The connection can be used to reconstruct the extrinsic curvature. The relation is given by
[math]\displaystyle{ A_a^i = \Gamma_a^i - i K_a^i }[/math]
where [math]\displaystyle{ \Gamma_a^i }[/math] is related to the spin connection, [math]\displaystyle{ \Gamma_{a \;\; i}^{\;\; j} }[/math], by [math]\displaystyle{ \Gamma_a^i = \Gamma_{ajk} \epsilon^{jki} }[/math] and [math]\displaystyle{ K_a^i = K_{ab} \tilde{E}^{ai} / \sqrt{\det (q)} }[/math].
In terms of Ashtekar variables the classical expression of the constraint is given by,
[math]\displaystyle{ H = {\epsilon_{ijk} F_{ab}^k \tilde{E}_i^a \tilde{E}_j^b \over \sqrt{\det (q)}}. }[/math]
where [math]\displaystyle{ F_{ab}^k }[/math] field strength tensor of the gauge field [math]\displaystyle{ A_a^i }[/math] . Due to the factor [math]\displaystyle{ 1 / \sqrt{\det (q)} }[/math] this is non-polynomial in the Ashtekar's variables. Since we impose the condition
[math]\displaystyle{ H = 0, }[/math]
we could consider the densitized Hamiltonian instead,
[math]\displaystyle{ \tilde{H} = \sqrt{\det (q)} H = \epsilon_{ijk} F_{ab}^k \tilde{E}_i^a \tilde{E}_j^b = 0. }[/math]
This Hamiltonian is now polynomial the Ashtekar's variables. This development raised new hopes for the canonical quantum gravity programme.[5] Although Ashtekar variables had the virtue of simplifying the Hamiltonian, it has the problem that the variables become complex. When one quantizes the theory it is a difficult task ensure that one recovers real general relativity as opposed to complex general relativity. Also there were also serious difficulties promoting the densitized Hamiltonian to a quantum operator.
A way of addressing the problem of reality conditions was noting that if we took the signature to be [math]\displaystyle{ (+,+,+,+) }[/math], that is Euclidean instead of Lorentzian, then one can retain the simple form of the Hamiltonian for but for real variables. One can then define what is called a generalized Wick rotation to recover the Lorentzian theory.[6] Generalized as it is a Wick transformation in phase space and has nothing to do with analytical continuation of the time parameter [math]\displaystyle{ t }[/math].
Expression for real formulation of Ashtekar variables
Thomas Thiemann addressed both the above problems.[4] He used the real connection
[math]\displaystyle{ A_a^i = \Gamma_a^i + \beta K_a^i }[/math]
In real Ashtekar variables the full Hamiltonian is
[math]\displaystyle{ H = - \zeta {\epsilon_{ijk} F_{ab}^k \tilde{E}_i^a \tilde{E}_j^b \over \sqrt{\det (q)}} + 2 {\zeta \beta^2 - 1 \over \beta^2} {(\tilde{E}_i^a \tilde{E}_j^b - \tilde{E}_j^a \tilde{E}_i^b) \over \sqrt{\det (q)}} (A_a^i - \Gamma_a^i) (A_b^j - \Gamma_b^j) = H_E + H'. }[/math]
where the constant [math]\displaystyle{ \beta }[/math] is the Barbero–Immirzi parameter.[7] The constant [math]\displaystyle{ \zeta }[/math] is -1 for Lorentzian signature and +1 for Euclidean signature. The [math]\displaystyle{ \Gamma_a^i }[/math] have a complicated relationship with the densitized triads and causes serious problems upon quantization. Ashtekar variables can be seen as choosing [math]\displaystyle{ \beta = i }[/math] to make the second more complicated term was made to vanish (the first term is denoted [math]\displaystyle{ H_E }[/math] because for the Euclidean theory this term remains for the real choice of [math]\displaystyle{ \beta = \pm 1 }[/math]). Also we still have the problem of the [math]\displaystyle{ 1 / \sqrt{\det (q)} }[/math] factor.
Thiemann was able to make it work for real [math]\displaystyle{ \beta }[/math]. First he could simplify the troublesome [math]\displaystyle{ 1 / \sqrt{\det (q)} }[/math] by using the identity
[math]\displaystyle{ \{ A_c^k , V \} = {\epsilon_{abc} \epsilon^{ijk} \tilde{E}_i^a \tilde{E}_j^b \over \sqrt{\det (q)}} }[/math]
where [math]\displaystyle{ V }[/math] is the volume,
[math]\displaystyle{ V = \int d^3 x \sqrt{\det (q)} = {1 \over 6} \int d^3 x \sqrt{\left|\tilde{E}_i^a \tilde{E}_j^b \tilde{E}_k^c \epsilon^{ijk} \epsilon_{abc}\right|}. }[/math]
The first term of the Hamiltonian constraint becomes
[math]\displaystyle{ H_E = \{ A_c^k , V \} F_{ab}^k \tilde{\epsilon}^{abc} }[/math]
upon using Thiemann's identity. This Poisson bracket is replaced by a commutator upon quantization. It turns out that a similar trick can be used to teat the second term. Why are the [math]\displaystyle{ \Gamma_a^i }[/math] given by the densitized triads [math]\displaystyle{ \tilde{E}^a_i }[/math]? It actually come about from the Gauss Law
[math]\displaystyle{ D_a \tilde{E}^a_i = 0. }[/math]
We can solve this in much the same way as the Levi-Civita connection can be calculated from the equation [math]\displaystyle{ \nabla_c g_{ab} = 0 }[/math]; by rotating the various indices and then adding and subtracting them. The result is complicated and non-linear. To circumvent the problems introduced by this complicated relationship Thiemann first defines the Gauss gauge invariant quantity
[math]\displaystyle{ K = \int d^3 x K_a^i \tilde{E}_i^a }[/math]
where [math]\displaystyle{ K_a^i = K_{ab} \tilde{E}^{ai} / \sqrt{\det (q)} }[/math], and notes that
[math]\displaystyle{ K_a^i = \{ A_a^i , K \}. }[/math]
We are then able to write
[math]\displaystyle{ A_a^i - \Gamma_a^i = \beta K_a^i = \beta \{ A_a^i , K \} }[/math]
and as such find an expression in terms of the configuration variable [math]\displaystyle{ A_a^i }[/math] and [math]\displaystyle{ K }[/math]. We obtain for the second term of the Hamiltonian
[math]\displaystyle{ H' = \epsilon^{abc} \epsilon_{ijk} \{ A_a^i , K \} \{ A_b^j , K \} \{ A_c^k , V \}. }[/math]
Why is it easier to quantize [math]\displaystyle{ K }[/math]? This is because it can be rewritten in terms of quantities that we already know how to quantize. Specifically [math]\displaystyle{ K }[/math] can be rewritten as
[math]\displaystyle{ K = - \left\{ V , \int d^3 x H_E \right\} }[/math]
where we have used that the integrated densitized trace of the extrinsic curvature is the "time derivative of the volume".
References
- ↑ Misner, Charles W.; Thorne, Kip S.; Wheeler, John Archibald. Gravitation. New York: W. H. Freeman and company.
- ↑ Ashtekar, Abhay (1986-11-03). "New Variables for Classical and Quantum Gravity". Physical Review Letters (American Physical Society (APS)) 57 (18): 2244–2247. doi:10.1103/physrevlett.57.2244. ISSN 0031-9007.
- ↑ Rovelli, Carlo; Smolin, Lee (1988-09-05). "Knot Theory and Quantum Gravity". Physical Review Letters (American Physical Society (APS)) 61 (10): 1155–1158. doi:10.1103/physrevlett.61.1155. ISSN 0031-9007.
- ↑ 4.0 4.1 Thiemann, T. (1996). "Anomaly-free formulation of non-perturbative, four-dimensional Lorentzian quantum gravity". Physics Letters B (Elsevier BV) 380 (3-4): 257–264. doi:10.1016/0370-2693(96)00532-1. ISSN 0370-2693.
- ↑ See the book Lectures on Non-Perturbative Canonical Gravity for more details on this and the subsequent development. First published in 1991. World Scientific Publishing Co. Pte. LtD.
- ↑ Thiemann, T (1996-06-01). "Reality conditions inducing transforms for quantum gauge field theory and quantum gravity". Classical and Quantum Gravity (IOP Publishing) 13 (6): 1383–1403. doi:10.1088/0264-9381/13/6/012. ISSN 0264-9381.
- ↑ Barbero G., J. Fernando (1995-05-15). "Real Ashtekar variables for Lorentzian signature space-times". Physical Review D (American Physical Society (APS)) 51 (10): 5507–5510. doi:10.1103/physrevd.51.5507. ISSN 0556-2821.
External links
 |
 KSF
KSF