Hard spheres

Hard spheres are widely used as model particles in the statistical mechanical theory of fluids and solids. They are defined simply as impenetrable spheres that cannot overlap in space. They mimic the extremely strong ("infinitely elastic bouncing") repulsion that atoms and spherical molecules experience at very close distances. Hard spheres systems are studied by analytical means, by molecular dynamics simulations, and by the experimental study of certain colloidal model systems. The hard-sphere system provides a generic model that explains the quasiuniversal structure and dynamics of simple liquids.^[1]

Beside being a model of theoretical significance, the hard-sphere system is used as a basis in the formulation of several modern, predictive Equations of State for real fluids through the SAFT approach, and models for transport properties in gases through Chapman-Enskog Theory.

Formal definition

Hard spheres of diameter [math]\displaystyle{ \sigma }[/math] are particles with the following pairwise interaction potential:

[math]\displaystyle{ V(\mathbf{r}_1,\mathbf{r}_2)=\left\{ \begin{matrix}0 & \mbox{if}\quad |\mathbf{r}_1-\mathbf{r}_2| \geq \sigma \\ \infty & \mbox{if}\quad|\mathbf{r}_1-\mathbf{r}_2| \lt \sigma \end{matrix} \right. }[/math]

where [math]\displaystyle{ \mathbf{r}_1 }[/math] and [math]\displaystyle{ \mathbf{r}_2 }[/math] are the positions of the two particles.

Hard-spheres gas

The first three virial coefficients for hard spheres can be determined analytically

[math]\displaystyle{ \frac{B_2}{v_0} }[/math]	=	[math]\displaystyle{ 4{\frac{}{}} }[/math]
[math]\displaystyle{ \frac{B_3}{{v_0}^2} }[/math]	=	[math]\displaystyle{ 10{\frac{}{}} }[/math]
[math]\displaystyle{ \frac{B_4}{{v_0}^3} }[/math]	=	[math]\displaystyle{ -\frac{712}{35}+\frac{219 \sqrt{2}}{35 \pi}+\frac{4131}{35 \pi} \arccos{\frac{1}{\sqrt{3}}}\approx 18.365 }[/math]

Higher-order ones can be determined numerically using Monte Carlo integration. We list

[math]\displaystyle{ \frac{B_5}{{v_0}^4} }[/math]	=	[math]\displaystyle{ 28.24 \pm 0.08 }[/math]
[math]\displaystyle{ \frac{B_6}{{v_0}^5} }[/math]	=	[math]\displaystyle{ 39.5 \pm 0.4 }[/math]
[math]\displaystyle{ \frac{B_7}{{v_0}^6} }[/math]	=	[math]\displaystyle{ 56.5 \pm 1.6 }[/math]

A table of virial coefficients for up to eight dimensions can be found on the page Hard sphere: virial coefficients.^[2]

Phase diagram of hard sphere system (Solid line - stable branch, dashed line - metastable branch): Pressure [math]\displaystyle{ P }[/math] as a function of the volume fraction (or packing fraction) [math]\displaystyle{ \eta }[/math]

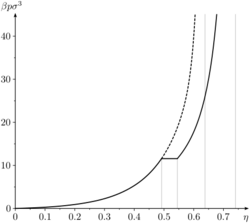
The hard sphere system exhibits a fluid-solid phase transition between the volume fractions of freezing [math]\displaystyle{ \eta_\mathrm{f}\approx 0.494 }[/math] and melting [math]\displaystyle{ \eta_\mathrm{m}\approx 0.545 }[/math]. The pressure diverges at random close packing [math]\displaystyle{ \eta_\mathrm{rcp}\approx 0.644 }[/math] for the metastable liquid branch and at close packing [math]\displaystyle{ \eta_\mathrm{cp}=\sqrt{2}\pi/6 \approx 0.74048 }[/math] for the stable solid branch.

Hard-spheres liquid

The static structure factor of the hard-spheres liquid can be calculated using the Percus–Yevick approximation.

The Carnahan-Starling Equation of State

A simple, yet popular equation of state describing systems of pure hard spheres was developed in 1969 by N. F. Carnahan and K. E. Starling.^[3] By expressing the compressibility of a hard-sphere system as a geometric series, the expression

[math]\displaystyle{ Z = \frac{pV}{nRT} = \frac{1 + \eta + \eta^2 - \eta^3}{(1 - \eta)^3} }[/math]

is obtained, where [math]\displaystyle{ \eta }[/math] is the packing fraction, given by

[math]\displaystyle{ \eta = \frac{N_A \pi n \sigma^3}{6V} }[/math]

where [math]\displaystyle{ N_A }[/math] is Avogadros number, [math]\displaystyle{ n / V }[/math] is the molar density of the fluid, and [math]\displaystyle{ \sigma }[/math] is the diameter of the hard-spheres. From this Equation of State, one can obtain the residual Helmholtz energy,^[4]

[math]\displaystyle{ \frac{A_{res}}{nRT} = \frac{4 \eta - 3 \eta^2}{( 1 - \eta )^2} }[/math],

which yields the residual chemical potential

[math]\displaystyle{ \frac{\mu_{res}}{RT} = \frac{8 \eta - 9 \eta^2 + 3 \eta^3}{(1 - \eta)^3} }[/math].

One can also obtain the value of the radial distribution function, [math]\displaystyle{ g(r) }[/math], evaluated at the surface of a sphere,^[4]

[math]\displaystyle{ g(\sigma) = \frac{1 - \frac{1}{2} \eta}{(1 - \eta)^3} }[/math].

The latter is of significant importance to accurate descriptions of more advanced intermolecular potentials based on perturbation theory, such as SAFT, where a system of hard spheres is taken as a reference system, and the complete pair-potential is described by perturbations to the underlying hard-sphere system. Computation of the transport properties of hard-sphere gases at moderate densities using Revised Enskog Theory also relies on an accurate value for [math]\displaystyle{ g(\sigma) }[/math], and the Carnahan-Starling Equation of State has been used for this purpose to large success.^[5]

See also

• Classical fluid

Literature

• J. P. Hansen and I. R. McDonald Theory of Simple Liquids Academic Press, London (1986)
• Hard sphere model page on SklogWiki.

References

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Hard spheres. Read more