Harmony
Topic: Physics
 From HandWiki - Reading time: 21 min
From HandWiki - Reading time: 21 min

In music, harmony is the concept of combining different sounds together in order to create new, distinct musical ideas.[1] Theories of harmony seek to describe or explain the effects created by distinct pitches or tones coinciding with one another; harmonic objects such as chords, textures and tonalities are identified, defined, and categorized in the development of these theories. Harmony is broadly understood to involve both a "vertical" dimension (frequency-space) and a "horizontal" dimension (time-space), and often overlaps with related musical concepts such as melody, timbre, and form.[2]
A particular emphasis on harmony is one of the core concepts underlying the theory and practice of Western music.[3] The study of harmony involves the juxtaposition of individual pitches to create chords, and in turn the juxtaposition of chords to create larger chord progressions. The principles of connection that govern these structures have been the subject of centuries worth of theoretical work and vernacular practice alike.[4]
Drawing both from music theoretical traditions and the field of psychoacoustics, its perception in large part consists of recognizing and processing consonance, a concept whose precise definition has varied throughout history, but is often associated with simple mathematical ratios between coincident pitch frequencies. In the physiological approach, consonance is viewed as a continuous variable measuring the human brain's ability to 'decode' aural sensory input. Culturally, consonant pitch relationships are often described as sounding more pleasant, euphonious, and beautiful than dissonant pitch relationships, which can be conversely characterized as unpleasant, discordant, or rough.[5]
In popular and jazz harmony, chords are named by their root plus various terms and characters indicating their qualities. In many types of music, notably baroque, romantic, modern, and jazz, chords are often augmented with "tensions". A tension is an additional chord member that creates a relatively dissonant interval in relation to the bass. The notion of counterpoint seeks to understand and describe the relationships between melodic lines, often in the context of a polyphonic texture of several simultaneous but independent voices. Therefore, it is sometimes seen as a type of harmonic understanding, and sometimes distinguished from harmony.[6]
Typically, in the classical common practice period a dissonant chord (chord with tension) "resolves" to a consonant chord. Harmonization usually sounds pleasant to the ear when there is a balance between consonance and dissonance. Simply put, this occurs when there is a balance between "tense" and "relaxed" moments. Dissonance is an important part of harmony when dissonance can be resolved and contribute to the composition of music as a whole. A misplayed note or any sound that is judged to detract from the whole composition can be described as disharmonious rather than dissonant.[1]
Etymology and definitions
The term harmony derives from the Greek ἁρμονία harmonia, meaning "joint, agreement, concord",[7][8] from the verb ἁρμόζω harmozō, "(Ι) fit together, join".[9] Aristoxenus wrote a work entitled Elements of Harmony, which is thought the first work in European history written on the subject of harmony.[10] In this book, Aristoxenus refers to previous experiments conducted by Pythagoreans to determine the relationship between small integer ratios and consonant notes (e.g., 1:2 describes an octave relationship, which is a doubling of frequency). While identifying as a Pythagorean, Aristoxenus claims that numerical ratios are not the ultimate determinant of harmony; instead, he claims that the listener's ear determines harmony.[11]
Current dictionary definitions, while attempting to give concise descriptions, often highlight the ambiguity of the term in modern use. Ambiguities tend to arise from either aesthetic considerations (for example the view that only pleasing concords may be harmonious) or from the point of view of musical texture (distinguishing between harmonic (simultaneously sounding pitches) and "contrapuntal" (successively sounding tones)).[12] According to A. Whittall:
The view that modern tonal harmony in Western music began in about 1600 is commonplace in music theory. This is usually accounted for by the replacement of horizontal (or contrapuntal) composition, common in the music of the Renaissance, with a new emphasis on the vertical element of composed music. Modern theorists, however, tend to see this as an unsatisfactory generalisation. According to Carl Dahlhaus:
Descriptions and definitions of harmony and harmonic practice often show bias towards European (or Western) musical traditions, although many cultures practice vertical harmony.[13] In addition, South Asian art music (Hindustani and Carnatic music) is frequently cited as placing little emphasis on what is perceived in western practice as conventional harmony; the underlying harmonic foundation for most South Asian music is the drone, a held open fifth interval (or fourth interval) that does not alter in pitch throughout the course of a composition.[14] Pitch simultaneity in particular is rarely a major consideration. Nevertheless, many other considerations of pitch are relevant to the music, its theory and its structure, such as the complex system of Ragas, which combines both melodic and modal considerations and codifications within it.[15]
So, intricate pitch combinations that sound simultaneously do occur in Indian classical music – but they are rarely studied as teleological harmonic or contrapuntal progressions – as with notated Western music. This contrasting emphasis (with regard to Indian music in particular) manifests itself in the different methods of performance adopted: in Indian Music, improvisation takes a major role in the structural framework of a piece,[16] whereas in Western Music improvisation has been uncommon since the end of the 19th century.[17] Where it does occur in Western music (or has in the past), the improvisation either embellishes pre-notated music or draws from musical models previously established in notated compositions, and therefore uses familiar harmonic schemes.[18]
Emphasis on the precomposed in European art music and the written theory surrounding it shows considerable cultural bias. The Grove Dictionary of Music and Musicians (Oxford University Press) identifies this clearly:
In Western culture the musics that are most dependent on improvisation, such as jazz, have traditionally been regarded as inferior to art music, in which pre-composition is considered paramount. The conception of musics that live in oral traditions as something composed with the use of improvisatory techniques separates them from the higher-standing works that use notation.[19]
Yet the evolution of harmonic practice and language itself, in Western art music, is and was facilitated by this process of prior composition, which permitted the study and analysis by theorists and composers of individual pre-constructed works in which pitches (and to some extent rhythms) remained unchanged regardless of the nature of the performance.[12]
Historical rules
Early Western religious music often features parallel perfect intervals; these intervals would preserve the clarity of the original plainsong. These works were created and performed in cathedrals, and made use of the resonant modes of their respective cathedrals to create harmonies. As polyphony developed, however, the use of parallel intervals was slowly replaced by the English style of consonance that used thirds and sixths.[when?] The English style was considered to have a sweeter sound, and was better suited to polyphony in that it offered greater linear flexibility in part-writing.

 Play (help·info) or
Play (help·info) or  Play harmony (help·info)
Play harmony (help·info)Types

 Play (help·info)
Play (help·info)
 Play (help·info)
Play (help·info)Carl Dahlhaus (1990) distinguishes between coordinate and subordinate harmony. Subordinate harmony is the hierarchical tonality or tonal harmony well known today. Coordinate harmony is the older Medieval and Renaissance tonalité ancienne, "The term is meant to signify that sonorities are linked one after the other without giving rise to the impression of a goal-directed development. A first chord forms a 'progression' with a second chord, and a second with a third. But the former chord progression is independent of the later one and vice versa." Coordinate harmony follows direct (adjacent) relationships rather than indirect as in subordinate. Interval cycles create symmetrical harmonies, which have been extensively used by the composers Alban Berg, George Perle, Arnold Schoenberg, Béla Bartók, and Edgard Varèse's Density 21.5.
Close harmony and open harmony use close position and open position chords, respectively. See: Voicing (music) and Close and open harmony.
Other types of harmony are based upon the intervals of the chords used in that harmony. Most chords in western music are based on "tertian" harmony, or chords built with the interval of thirds. In the chord C Major7, C–E is a major third; E–G is a minor third; and G to B is a major third. Other types of harmony consist of quartal and quintal harmony.
A unison is considered a harmonic interval, just like a fifth or a third, but is unique in that it is two identical notes produced together. The unison, as a component of harmony, is important, especially in orchestration.[20] In pop music, unison singing is usually called doubling, a technique The Beatles used in many of their earlier recordings. As a type of harmony, singing in unison or playing the same notes, often using different musical instruments, at the same time is commonly called monophonic harmonization.
Intervals
An interval is the relationship between two separate musical pitches. For example, in the melody "Twinkle Twinkle Little Star", between the first two notes (the first "twinkle") and the second two notes (the second "twinkle") is the interval of a fifth. What this means is that if the first two notes were the pitch C, the second two notes would be the pitch G—four scale notes, or seven chromatic notes (a perfect fifth), above it.
The following are common intervals:
| Root | Major third | Minor third | Fifth |
|---|---|---|---|
| C | E | G | |
| F | |||
| D | F | A | |
| G | |||
| E | G | B | |
| F | A | C | |
| A | |||
| G | B | D | |
| C | |||
| A | C | E | |
| D | F | ||
| B | D |
When tuning notes using an equal temperament, such as the 12-tone equal temperament that has become ubiquitous in Western music, each interval is created using steps of the same size, producing harmonic relations marginally 'out of tune' from pure frequency ratios as explored by the ancient Greeks. 12-tone equal temperament evolved as a compromise from earlier systems where all intervals were calculated relative to a chosen root frequency, such as just intonation and well temperament. In those systems, a major third constructed up from C did not produce the same frequency as a minor third constructed up from D♭. Many keyboard and fretted instruments were constructed with the ability to play, for example, both of G♯ and A♭ without retuning. The notes of these pairs (even those where one lacks an accidental, such as E and F♭) were not the 'same' note in any sense.
Using the diatonic scale, constructing the major and minor keys with each of the 12 notes as the tonic can be achieved using only flats or sharps to spell notes within said key, never both. This is often visualized as traveling around the circle of fifths, with each step only involving a change in one note's accidental. As such, additional accidentals are free to convey more nuanced information in the context of a passage of music and the other notes that make it up. Even when working outside diatonic contexts, it is convention, if possible, to use each letter in the alphabet only once in describing a scale.
Importantly, a note spelled as F♭ conveys different harmonic information to the reader versus a note spelled as E. In a tuning system where two notes spelled differently are tuned to the same frequency, those notes are said to be enharmonic. Even if identical in isolation, different spellings of enharmonic notes provide meaningful context when reading and analyzing music. For example, even though E and F♭ are enharmonic, the former is considered to be a major third up from C, while F♭ is considered to be a diminished fourth up from C. In the context of a C major tonality, the former is the third of the scale, while the latter could (as one of numerous possible justifications) be serving the harmonic function of the third of a D♭ minor chord, a borrowed chord within the scale.
Therefore, the combination of notes with their specific intervals—a chord—creates harmony.[21] For example, in a C chord, there are three notes: C, E, and G. The note C is the root. The notes E and G provide harmony, and in a G7 (G dominant 7th) chord, the root G with each subsequent note (in this case B, D and F) provide the harmony.[21]
In the musical scale, there are twelve pitches. Each pitch is referred to as a "degree" of the scale. The names A, B, C, D, E, F, and G are insignificant.[22] The intervals, however, are not. Here is an example:
| 1° | 2° | 3° | 4° | 5° | 6° | 7° | 8° |
|---|---|---|---|---|---|---|---|
| C | D | E | F | G | A | B | C |
| D | E | G | A | B | D |
As can be seen, no note will always be the same scale degree. The tonic, or first-degree note, can be any of the 12 notes (pitch classes) of the chromatic scale. All the other notes fall into place. For example, when C is the tonic, the fourth degree or subdominant is F. When D is the tonic, the fourth degree is G. While the note names remain constant, they may refer to different scale degrees, implying different intervals with respect to the tonic. The great power of this fact is that any musical work can be played or sung in any key. It is the same piece of music, as long as the intervals are the same—thus transposing the melody into the corresponding key. When the intervals surpass the perfect Octave (12 semitones), these intervals are called compound intervals, which include particularly the 9th, 11th, and 13th Intervals—widely used in jazz and blues Music.[23]
Compound Intervals are formed and named as follows:
- 2nd + Octave = 9th
- 3rd + Octave = 10th
- 4th + Octave = 11th
- 5th + Octave = 12th
- 6th + Octave = 13th
- 7th + Octave = 14th
These numbers don't "add" together because intervals are numbered inclusive of the root note (e.g. one tone up is a 2nd), so the root is counted twice by adding them. Apart from this categorization, intervals can also be divided into consonant and dissonant. As explained in the following paragraphs, consonant intervals produce a sensation of relaxation and dissonant intervals a sensation of tension. In tonal music, the term consonant also means "brings resolution" (to some degree at least, whereas dissonance "requires resolution").[citation needed]
The consonant intervals are considered the perfect unison, octave, fifth, fourth and major and minor third and sixth, and their compound forms. An interval is referred to as "perfect" when the harmonic relationship is found in the natural overtone series (namely, the unison 1:1, octave 2:1, fifth 3:2, and fourth 4:3). The other basic intervals (second, third, sixth, and seventh) are called "imperfect" because the harmonic relationships are not found mathematically exact in the overtone series. In classical music the perfect fourth above the bass may be considered dissonant when its function is contrapuntal. Other intervals, the second and the seventh (and their compound forms) are considered Dissonant and require resolution (of the produced tension) and usually preparation (depending on the music style[24]).
The effect of dissonance is perceived relatively within musical context: for example, a major seventh interval alone (i.e., C up to B) may be perceived as dissonant, but the same interval as part of a major seventh chord may sound relatively consonant. A tritone (the interval of the fourth step to the seventh step of the major scale, i.e., F to B) sounds very dissonant alone, but less so within the context of a dominant seventh chord (G7 or D♭7 in that example).[25]
Chords and tension
In the Western tradition, in music after the seventeenth century, harmony is manipulated using chords, which are combinations of pitch classes. In tertian harmony, so named after the interval of a third, the members of chords are found and named by stacking intervals of the third, starting with the "root", then the "third" above the root, and the "fifth" above the root (which is a third above the third), etc. (Chord members are named after their interval above the root.) Dyads, the simplest chords, contain only two members (see power chords).
A chord with three members is called a triad because it has three members, not because it is necessarily built in thirds (see Quartal and quintal harmony for chords built with other intervals). Depending on the size of the intervals being stacked, different qualities of chords are formed. In popular and jazz harmony, chords are named by their root plus various terms and characters indicating their qualities. To keep the nomenclature as simple as possible, some defaults are accepted (not tabulated here). For example, the chord members C, E, and G, form a C Major triad, called by default simply a C chord. In an A♭ chord (pronounced A-flat), the members are A♭, C, and E♭.
In many types of music, notably baroque, romantic, modern and jazz, chords are often augmented with "tensions". A tension is an additional chord member that creates a relatively dissonant interval in relation to the bass. Following the tertian practice of building chords by stacking thirds, the simplest first tension is added to a triad by stacking, on top of the existing root, third, and fifth, another third above the fifth, adding a new, potentially dissonant member a seventh away from the root (called the "seventh" of the chord) producing a four-note chord called a "seventh chord".
Depending on the widths of the individual thirds stacked to build the chord, the interval between the root and the seventh of the chord may be major, minor, or diminished. (The interval of an augmented seventh reproduces the root, and is therefore left out of the chordal nomenclature.) The nomenclature allows that, by default, "C7" indicates a chord with a root, third, fifth, and seventh spelled C, E, G, and B♭. Other types of seventh chords must be named more explicitly, such as "C Major 7" (spelled C, E, G, B), "C augmented 7" (here the word augmented applies to the fifth, not the seventh, spelled C, E, G♯, B♭), etc. (For a more complete exposition of nomenclature see Chord (music).)
Continuing to stack thirds on top of a seventh chord produces extensions, and brings in the "extended tensions" or "upper tensions" (those more than an octave above the root when stacked in thirds), the ninths, elevenths, and thirteenths. This creates the chords named after them. (Except for dyads and triads, tertian chord types are named for the interval of the largest size and magnitude in use in the stack, not for the number of chord members : thus a ninth chord has five members [tonic, 3rd, 5th, 7th, 9th], not nine.) Extensions beyond the thirteenth reproduce existing chord members and are (usually) left out of the nomenclature. Complex harmonies based on extended chords are found in abundance in jazz, late-romantic music, modern orchestral works, film music, etc.
Typically, in the classical Common practice period a dissonant chord (chord with tension) resolves to a consonant chord. Harmonization usually sounds pleasant to the ear when there is a balance between the consonant and dissonant sounds. In simple words, that occurs when there is a balance between "tense" and "relaxed" moments. For this reason, usually tension is 'prepared' and then 'resolved',[26] where preparing tension means to place a series of consonant chords that lead smoothly to the dissonant chord. In this way the composer ensures introducing tension smoothly, without disturbing the listener. Once the piece reaches its sub-climax, the listener needs a moment of relaxation to clear up the tension, which is obtained by playing a consonant chord that resolves the tension of the previous chords. The clearing of this tension usually sounds pleasant to the listener, though this is not always the case in late-nineteenth century music, such as Tristan und Isolde by Richard Wagner.[26]
Perception
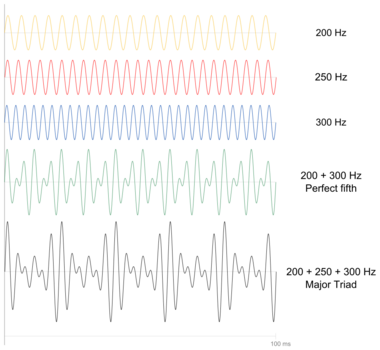
A number of features contribute to the perception of a chord's harmony.
Tonal fusion
Tonal fusion contributes to the perceived consonance of a chord,[27] describing the degree to which multiple pitches are heard as a single, unitary tone.[27] Chords which have more coinciding partials (frequency components) are perceived as more consonant, such as the octave and perfect fifth. The spectra of these intervals resemble that of a uniform tone. According to this definition, a major triad fuses better than a minor triad and a major-minor seventh chord fuses better than a major-major seventh or minor-minor seventh. These differences may not be readily apparent in tempered contexts but can explain why major triads are generally more prevalent than minor triads and major-minor sevenths are generally more prevalent than other sevenths (in spite of the dissonance of the tritone interval) in mainstream tonal music.
In organ registers, certain harmonic interval combinations and chords are activated by a single key. The sounds produced fuse into one tone with a new timbre. This tonal fusion effect is also used in synthesizers and orchestral arrangements; for instance, in Ravel's Bolero #5 the parallel parts of flutes, horn and celesta resemble the sound of an electric organ.[28][29]
Roughness
When adjacent harmonics in complex tones interfere with one another, they create the perception of what is known as "beating" or "roughness". These precepts are closely related to the perceived dissonance of chords.[30] To interfere, partials must lie within a critical bandwidth, which is a measure of the ear's ability to separate different frequencies.[31] Critical bandwidth lies between 2 and 3 semitones at high frequencies and becomes larger at lower frequencies.[32] The roughest interval in the chromatic scale is the minor second and its inversion, the major seventh. For typical spectral envelopes in the central range, the second roughest interval is the major second and minor seventh, followed by the tritone, the minor third (major sixth), the major third (minor sixth) and the perfect fourth (fifth).[33]
Familiarity
Familiarity also contributes to the perceived harmony of an interval. Chords that have often been heard in musical contexts tend to sound more consonant. This principle explains the gradual historical increase in harmonic complexity of Western music. For example, around 1600 unprepared seventh chords gradually became familiar and were therefore gradually perceived as more consonant.[34]
Individual characteristics such as age and musical experience also have an effect on harmony perception.[35][36]
Neural correlates of harmony
The inferior colliculus is a mid-brain structure which is the first site of binaural auditory integration, processing auditory information from the left and right ears.[37] Frequency following responses (FFRs) recorded from the mid-brain exhibit peaks in activity which correspond to the frequency components of a tonal stimulus.[36] The extent to which FFRs accurately represent the harmonic information of a chord is called neural salience, and this value is correlated with behavioral ratings of the perceived pleasantness of chords.[36]
In response to harmonic intervals, cortical activity also distinguishes chords by their consonance, responding more robustly to chords with greater consonance.[27]
Consonance and dissonance in balance
The creation and destruction of harmonic and 'statistical' tensions is essential to the maintenance of compositional drama. Any composition (or improvisation) which remains consistent and 'regular' throughout is, for me, equivalent to watching a movie with only 'good guys' in it, or eating cottage cheese.
— Frank Zappa, The Real Frank Zappa Book, page 181, Frank Zappa and Peter Occhiogrosso, 1990
See also
- Chromatic chord
- Chromatic mediant
- Harmonie
- Homophony (music)
- List of musical terminology
- Mathematics of musical scales
- Musica universalis
- Organum (polyphonic chant)
- Peter Westergaard's tonal theory
- Physics of music
- Prolongation
- Tonality
- Unified field
- Voice leading
References
Footnotes
- ↑ 1.0 1.1 Lomas, J. Derek; Xue, Haian (1 March 2022). "Harmony in Design: A Synthesis of Literature from Classical Philosophy, the Sciences, Economics, and Design". She Ji: The Journal of Design, Economics, and Innovation 8 (1): 5–64. doi:10.1016/j.sheji.2022.01.001.
- ↑ Chan, Paul Yaozhu; Dong, Minghui; Li, Haizhou (29 September 2019). "The Science of Harmony: A Psychophysical Basis for Perceptual Tensions and Resolutions in Music". Research 2019: 1–22. doi:10.34133/2019/2369041. PMID 32043080.
- ↑ Malm, William P. (1996). Music Cultures of the Pacific, the Near East, and Asia, p. 15. ISBN 0-13-182387-6. Third edition. "Homophonic texture...is more common in Western music, where tunes are often built on chords (harmonies) that move in progressions. Indeed this harmonic orientation is one of the major differences between Western and much non-Western music."
- ↑ Dahlhaus, Car (2001). "Harmony". in Root, Deane L.. The New Grove Dictionary of Music and Musicians. Oxford University Press.
- ↑ "Musical building blocks". https://www.ismtrust.org/resources/primary-toolkit/composing-improvising-and-doodling/musical-building-blocks.
- ↑ Sachs, Klaus-Jürgen; Dahlhaus, Carl (2001). Counterpoint. Oxford University Press. doi:10.1093/gmo/9781561592630.article.06690. ISBN 9781561592630.
- ↑ "1. Harmony". 1. Harmony. Oxford Reference Online. http://www.oxfordreference.com/. Retrieved 24 February 2007.
- ↑ ἁρμονία. Liddell, Henry George; Scott, Robert; A Greek–English Lexicon at the Perseus Project.
- ↑ ἁρμόζω in Liddell and Scott.
- ↑ Aristoxenus (1902). Harmonika Stoicheia (The Harmonics of Aristoxenus). Georg Olms Verlag. ISBN 3487405105. OCLC 123175755. https://books.google.com/books?id=3TseQjV_wogC&pg=PA165.
- ↑ Barker, Andrew (November 1978). "Music and perception: a study in Aristoxenus". The Journal of Hellenic Studies 98: 9–16. doi:10.2307/630189.
- ↑ 12.0 12.1 Whittall, Arnold (2002). "Harmony". in Latham, Alison. The Oxford Companion to Music. Oxford University Press. ISBN 978-0-19-957903-7. http://www.oxfordreference.com/views/ENTRY.html?ubview=Main&entry=t114.e3144.
- ↑ Stone, Ruth (1998). Garland Encyclopedia of World Music vol. I Africa. New York and London: garland. ISBN 0-8240-6035-0.
- ↑ Qureshi, Regula (2001). "India, §I, 2(ii): Music and musicians: Art music". in Root, Deane L.. The New Grove Dictionary of Music and Musicians. Oxford University Press. and Catherine Schmidt Jones, 'Listening to Indian Classical Music', Connexions, (accessed 16 November 2007) [1]
- ↑ Powers, Harold S.; Widdess, Richard (2001). "India, §III, 2: Theory and practice of classical music: Rāga". in Root, Deane L.. The New Grove Dictionary of Music and Musicians. Oxford University Press.
- ↑ Powers, Harold S.; Widdess, Richard (2001). "Theory and practice of classical music: Melodic elaboration". in Root, Deane L.. The New Grove Dictionary of Music and Musicians. Oxford University Press. India, §III, 3(ii).
- ↑ Wegman, Rob C. (2001). "Western art music". in Root, Deane L.. The New Grove Dictionary of Music and Musicians. Oxford University Press. Improvisation, §II.
- ↑ Levin, Robert D. (2001). "The Classical period in Western art music: Instrumental music". in Root, Deane L.. The New Grove Dictionary of Music and Musicians. Oxford University Press. Improvisation, §II, 4(i).
- ↑ Nettl, Bruno (2001). "Concepts and practices: Improvisation in musical cultures". in Root, Deane L.. The New Grove Dictionary of Music and Musicians. Oxford University Press. Improvisation, §I, 2.
- ↑ Dahlhaus, Carl (2001). "Harmony". in Root, Deane L.. The New Grove Dictionary of Music and Musicians. Oxford University Press.
- ↑ 21.0 21.1 Jamini, Deborah (2005). Harmony and Composition: Basics to Intermediate, p. 147. ISBN 1-4120-3333-0.
- ↑ Ghani, Nour Abd. "The 12 Golden notes is all it takes...". https://www.skytopia.com/project/scale.html.
- ↑ STEFANUK, MISHA V. (2010-10-07). Jazz Piano Chords. Mel Bay Publications. ISBN 978-1-60974-315-4. https://books.google.com/books?id=JolkN10wM78C&q=Compound+intervals&pg=PA9.
- ↑ Peter Pesic. "Music and the Making of Modern Science". https://issuu.com/376746/docs/music_and_the_making_of_modern_-_pesic__peter_5685.
- ↑ "Intervals | Music Appreciation". https://courses.lumenlearning.com/musicappreciation_with_theory/chapter/interacting-with-intervals-and-scales/.
- ↑ 26.0 26.1 Schejtman, Rod (2008). The Piano Encyclopedia's "Music Fundamentals eBook", pp. 20–43 (accessed 10 March 2009) PianoEncyclopedia.com
- ↑ 27.0 27.1 27.2 Bidelman, Gavin M. (2013). "The Role of the Auditory Brainstem in Processing Musically Relevant Pitch". Frontiers in Psychology 4: 264. doi:10.3389/fpsyg.2013.00264. ISSN 1664-1078. PMID 23717294.
- ↑ Tanguiane (Tangian), Andranick (1993). Artificial Perception and Music Recognition. Lecture Notes in Artificial Intelligence. 746. Berlin-Heidelberg: Springer. ISBN 978-3-540-57394-4.
- ↑ Tanguiane (Tangian), Andranick (1994). "A principle of correlativity of perception and its application to music recognition". Music Perception 11 (4): 465–502. doi:10.2307/40285634.
- ↑ Langner, Gerald; Ochse, Michael (2006). "The neural basis of pitch and harmony in the auditory system". Musicae Scientiae 10 (1_suppl): 185–208. doi:10.1177/102986490601000109. ISSN 1029-8649. http://dx.doi.org/10.1177/102986490601000109.
- ↑ Plomp, R.; Levelt, W. J. M. (1965). "Tonal Consonance and Critical Bandwidth". The Journal of the Acoustical Society of America 38 (4): 548–560. doi:10.1121/1.1909741. ISSN 0001-4966. PMID 5831012. Bibcode: 1965ASAJ...38..548P. http://dx.doi.org/10.1121/1.1909741.
- ↑ Schellenberg, E. Glenn; Trehub, Sandra E. (1994). "Frequency ratios and the perception of tone patterns". Psychonomic Bulletin & Review 1 (2): 191–201. doi:10.3758/bf03200773. ISSN 1069-9384. PMID 24203470.
- ↑ Parncutt, Richard (1988). "Revision of Terhardt's Psychoacoustical Model of the Root(s) of a Musical Chord". Music Perception 6 (1): 65–93. doi:10.2307/40285416. ISSN 0730-7829. http://dx.doi.org/10.2307/40285416.
- ↑ Parncutt, Richard (2011). "The Tonic as Triad: Key Profiles as Pitch Salience Profiles of Tonic Triads". Music Perception 28 (4): 333–366. doi:10.1525/mp.2011.28.4.333. ISSN 0730-7829. http://dx.doi.org/10.1525/mp.2011.28.4.333.
- ↑ Bidelman, Gavin M.; Gandour, Jackson T.; Krishnan, Ananthanarayan (2011). "Musicians demonstrate experience-dependent brainstem enhancement of musical scale features within continuously gliding pitch". Neuroscience Letters 503 (3): 203–207. doi:10.1016/j.neulet.2011.08.036. ISSN 0304-3940. PMID 21906656.
- ↑ 36.0 36.1 36.2 Bones, O.; Plack, C. J. (2015-03-04). "Losing the Music: Aging Affects the Perception and Subcortical Neural Representation of Musical Harmony". Journal of Neuroscience 35 (9): 4071–4080. doi:10.1523/jneurosci.3214-14.2015. ISSN 0270-6474. PMID 25740534.
- ↑ Ito, Tetsufumi; Bishop, Deborah C.; Oliver, Douglas L. (2015-10-26). "Functional organization of the local circuit in the inferior colliculus". Anatomical Science International 91 (1): 22–34. doi:10.1007/s12565-015-0308-8. ISSN 1447-6959. PMID 26497006.
Citations
- Dahlhaus, Carl. Gjerdingen, Robert O. trans. (1990). Studies in the Origin of Harmonic Tonality, p. 141. Princeton University Press. ISBN 0-691-09135-8.
- van der Merwe, Peter (1989). Origins of the Popular Style: The Antecedents of Twentieth-Century Popular Music. Oxford: Clarendon Press. ISBN 0-19-316121-4.
- Nettles, Barrie & Graf, Richard (1997). The Chord Scale Theory and Jazz Harmony. Advance Music, ISBN 3-89221-056-X
Further reading
- Prout, Ebenezer, Harmony, its Theory and Practice (1889, revised 1903)
External links
 |
 KSF
KSF