Light field microscopy

Light field microscopy (LFM) is a scanning-free 3-dimensional (3D) microscopic imaging method based on the theory of light field. This technique allows sub-second (~10 Hz) large volumetric imaging ([~0.1 to 1 mm]³) with ~1 μm spatial resolution in the condition of weak scattering and semi-transparence, which has never been achieved by other methods. Just as in traditional light field rendering, there are two steps for LFM imaging: light field capture and processing. In most setups, a microlens array is used to capture the light field. As for processing, it can be based on two kinds of representations of light propagation: the ray optics picture^[1] and the wave optics picture.^[2] The Stanford University Computer Graphics Laboratory published their first prototype LFM in 2006^[1] and has been working on the cutting edge since then.

Light field generation

Ray parameterization of the light field microscopy. (A) Light field parameterization without any relay lens. The object plane conjugates with the microlens array plane via the objective, and the objective plane conjugates with the sensor plane via microlenses: the intermediate image of two points is on the microlens array plane, one microlens corresponding to one point; each subimage behind the corresponding microlens incorporates an image of the objective. (B) Light field parameterization with a relay system. The conjugation between points on the focal plane and mirolenses still remains; however, the subimage behind each microlens only incorporates a part of the objective. In both systems, a ray is parameterized as a combination of a 2D coordinate of the microlens through which the ray passes and a 2D coordinate of the subimage pixel on which it falls.

A light field is a collection of all the rays flowing through some free space, where each ray can be parameterized with four variables.^[3] In many cases, two 2D coordinates–denoted as [math]\displaystyle{ (s,t) }[/math] & [math]\displaystyle{ (u,v) }[/math]–on two parallel planes with which the rays intersect are applied for parameterization. Accordingly, the intensity of the 4D light field can be described as a scalar function: [math]\displaystyle{ L_f(s,t,u,v) }[/math], where [math]\displaystyle{ f }[/math] is the distance between two planes.

LFM can be built upon the traditional setup of a wide-field fluorescence microscope and a standard CCD camera or sCMOS.^[1] A light field is generated by placing a microlens array at the intermediate image plane of the objective (or the rear focal plane of an optional relay lens) and is further captured by placing the camera sensor at the rear focal plane of the microlenses. As a result, the coordinates of the microlenses [math]\displaystyle{ (s,t) }[/math] conjugate with those on the object plane (if additional relay lenses are added, then on the front focal plane of the objective) [math]\displaystyle{ (s',t') }[/math]; the coordinates of the pixels behind each microlens [math]\displaystyle{ (u,v) }[/math] conjugate with those on the objective plane [math]\displaystyle{ (u',v') }[/math]. For uniformity and convenience, we shall call the plane [math]\displaystyle{ (s',t') }[/math] the original focus plane in this article. Correspondingly, [math]\displaystyle{ f }[/math] is the focal length of the microlenses (i.e., the distance between microlens array plane and the sensor plane).

In addition, the apertures and the focal-length of each lens and the dimensions of the sensor and microlens array should all be properly chosen to ensure that there is neither overlap nor empty areas between adjacent subimages behind the corresponding microlenses.

Realization from the ray optics picture

This section mainly introduces the work of Levoy et al., 2006.^[1]

Perspective views from varied angles

Owing to the conjugated relationships as mentioned above, any certain pixel [math]\displaystyle{ (u_j,v_j) }[/math] behind a certain microlens [math]\displaystyle{ (s_i,t_i) }[/math] corresponds to the ray passing through the point [math]\displaystyle{ (s_i',t_i') }[/math] towards the direction [math]\displaystyle{ (u_j',v_j') }[/math]. Therefore, by extracting the pixel [math]\displaystyle{ (u_j,v_j) }[/math] from all subimages and stitching them together, a perspective view from the certain angle is obtained: [math]\displaystyle{ L_f(:,:,u_j,v_j) }[/math]. In this scenario, spatial resolution is determined by the number of microlenses; angular resolution is determined by the number of pixels behind each microlens.

Tomographic views based on synthetic refocusing

Step 1: Digital refocusing

Digital refocus of light field. Assume the original image has been focused on the plane that conjugates with the microlens array plane, thus the image should be synthesized by summing pixels behind each microlens to proform a digital focusing on this plane. Now, we want to refocus onto another plane whose conjugated plane is αf away from the sensor plane by rendering the rays defined between the microlens array plane and the sensor plane. To get the intensity of each point on the refocus plane, we sum the rays whose reverse extension lines end up at this point. This figure is the demonstration of a 1-dimension synthetic refocus, and the other dimension can be independently refocused in the same mathematical manner. This figure is a modification of Fig. 1 in Ren Ng 2005.^[4]

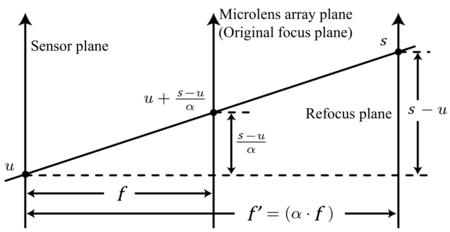
Synthetic focusing uses the captured light field to compute the photograph focusing at any arbitrary section. By simply summing all the pixels in each subimage behind the microlens (equivalent to collecting all radiation coming from different angles that falls on the same position), the image is focused exactly on the plane that conjugates with the microlens array plane:

[math]\displaystyle{ E_f(s,t)={1 \over f^2}\iint L_f(s,t,u,v)\cos^4\phi~dudv }[/math],

where [math]\displaystyle{ \phi }[/math] is the angle between the ray and the normal of the sensor plane, and [math]\displaystyle{ \phi=\arctan(\sqrt{u^2+v^2}/f) }[/math] if the origin of the coordinate system of each subimage is located on the principal optic axis of the corresponding microlens. Now, a new function can defined to absorb the effective projection factor [math]\displaystyle{ \cos^4\phi }[/math] into the light field intensity [math]\displaystyle{ L_{f} }[/math] and obtain the actual radiance collection of each pixel: [math]\displaystyle{ \bar{L}_f=L_f\cos^4\phi }[/math].

In order to focus on some other plane besides the front focal plane of the objective, say, the plane whose conjugated plane is [math]\displaystyle{ f'=\alpha f }[/math] away from the sensor plane, the conjugated plane can be moved from [math]\displaystyle{ f }[/math] to [math]\displaystyle{ \alpha f }[/math] and reparameterize its light field back to the original one at [math]\displaystyle{ f }[/math]:

[math]\displaystyle{ \bar{L}_{\alpha f}(s,t,u,v)=\bar{L}_f(u+(s-u)/\alpha,v+(t-v)/\alpha,u,v) }[/math].

Thereby, the refocused photograph can be computed with the following formula:

[math]\displaystyle{ E_{\alpha f}(s,t)={1 \over \alpha^2 f^2}\iint \bar{L}_f(u(1-1/\alpha)+s/\alpha,v(1-1/\alpha)+t/\alpha,u,v)~dudv }[/math].

Consequently, a focal stack is generated to recapitulate the instant 3D imaging of the object space. Furthermore, tilted or even curved focal planes are also synthetically possible.^[5] In addition, any reconstructed 2D image focused at an arbitrary depth corresponds to a 2D slice of a 4D light field in the Fourier domain, where the algorithm complexity can be reduced from [math]\displaystyle{ O(n^4) }[/math] to [math]\displaystyle{ O(n^2\log n) }[/math].^[4]

Step 2: Point spread function measurement

Due to diffraction and defocus, however, the focal stack [math]\displaystyle{ FS }[/math] differs from the actual intensity distribution of voxels [math]\displaystyle{ V }[/math], which is really desired. Instead, [math]\displaystyle{ FS }[/math] is a convolution of [math]\displaystyle{ V }[/math] and a point spread function (PSF):

[math]\displaystyle{ V*PSF=FS. }[/math]

Thus, the 3D shape of the PSF has to be measured in order to subtract its effect and to obtain voxels' net intensity. This measurement can be easily done by placing a fluorescent bead at the center of the original focus plane and recording its light field, based on which the PSF's 3D shape is ascertained by synthetically focusing on varied depth. Given that the PSF is acquired with the same LFM setup and digital refocusing procedure as the focal stack, this measurement correctly reflects the angular range of rays captured by the objective (including any falloff in intensity); therefore, this synthetic PSF is actually free of noise and aberrations. The shape of the PSF can be considered identical everywhere within our desired field of view (FOV); hence, multiple measurements can be avoided.

Step 3: 3D deconvolution

In the Fourier domain, the actual intensity of voxels has a very simple relation with the focal stack and the PSF:

[math]\displaystyle{ \mathcal{F}(V)=\frac{\mathcal{F}(FS)}{\mathcal{F}(PSF)} }[/math],

where [math]\displaystyle{ \mathcal{F} }[/math] is the operator of the Fourier transform. However, it may not be possible to directly solve the equation above, given the fact that the aperture is of limited size, resulting in the PSF being bandlimited (i.e., its Fourier transform has zeros). Instead, an iterative algorithm called constrained iterative deconvolution in the spatial domain is much more practical here:^[6]

1. [math]\displaystyle{ \bigtriangleup^{(k+1)}~\leftarrow~FS-V^{(k)}*PSF }[/math];
2. [math]\displaystyle{ V^{(k+1)}~\leftarrow~\max(V^{(k)}+\bigtriangleup^{(k+1)},0) }[/math].

This idea is based on constrained gradient descent: the estimation of [math]\displaystyle{ V }[/math] is improved iteratively by calculating the difference between the actual focal stack [math]\displaystyle{ FS }[/math] and the estimated focal stack [math]\displaystyle{ V*PSF }[/math] and correcting [math]\displaystyle{ V }[/math] with the current difference ([math]\displaystyle{ V }[/math] is constrained to be non-negative).

Fourier Slice Photography

The formula of [math]\displaystyle{ E_{\alpha f}(s,t) }[/math] can be rewritten by adopting the concept of the Fourier Projection-Slice Theorem.^[7] Because the photography operator [math]\displaystyle{ \mathcal{P}_\alpha[\bar{L_f}](s,t)=E_{\alpha f}(s,t) }[/math] can be viewed as a shear followed by projection, the result should be proportional to a dilated 2D slice of the 4D Fourier transform of a light field. Precisely, a refocused image can be generated from the 4D Fourier spectrum of a light field by extracting an 2D slice, applying an inverse 2D transform, and scaling. Before the proof, we first introduce some operators:

1. Integral Projection Operator: [math]\displaystyle{ \mathcal{I}^N_M[f](x_1,...,x_M)=\int{f(x_1,...,x_N)dx_{M+1}...dx_{N}} }[/math]
2. Slicing operator: [math]\displaystyle{ \mathcal{S}^N_M[f](x_1,...,x_M)=f(x_1,...,x_M,0,...,0) }[/math]
3. Photography Change of Basis: Let [math]\displaystyle{ \mathcal{B}_\alpha }[/math] denote an operator for a change of basis of an 4-dimensional function so that [math]\displaystyle{ \mathcal{B}[f](\mathrm{x})=f(\mathcal{B}^{-1}\mathrm{x}) }[/math], with [math]\displaystyle{ \mathcal{B}_\alpha=\begin{bmatrix} \alpha & 0 & 1-\alpha& 0 \\ 0 & \alpha & 0 & 1-\alpha\\ 0&0&1&0\\0&0&0&1\end{bmatrix} }[/math].
4. Fourier Transform Operator: Let [math]\displaystyle{ \mathcal{F}^N }[/math] denote the N-dimensional Fourier transform operator.

By these definitions, we can rewrite [math]\displaystyle{ \mathcal{P}_\alpha[\bar{L_f}](s,t)={1 \over \alpha^2 f^2}\iint \bar{L}_f(u(1-1/\alpha)+s/\alpha,v(1-1/\alpha)+t/\alpha,u,v)~dudv\equiv\frac{1}{\alpha^2f^2}\mathcal{I}^4_2\circ\mathcal{B}_\alpha[L_f] }[/math].

According to the generalized Fourier-slice theorem,^[7] we have

[math]\displaystyle{ \mathcal{F}^M\circ\mathcal{I}^N_M\circ\mathcal{B}\equiv\mathcal{S}^N_M\circ\frac{\mathcal{B}^{-T}}{|\mathcal{B}^{-T}|}\circ\mathcal{F}^N }[/math],

and hence the photography operator has the form

[math]\displaystyle{ \mathcal{P}_\alpha[\bar{L_f}](s,t)\equiv\frac{1}{f^2}\mathcal{F}^{-2}\circ\mathcal{S}^4_2\circ\mathcal{B}_\alpha^{-T}\circ\mathcal{F}^4 }[/math].

According to the formula, we know a photograph is the inverse 2D Fourier transform of a dilated 2D slice in the 4D Fourier transform of the light field.

Discrete Fourier Slice Photography

If all we have available are samples of the light field, instead of use Fourier slice theorem for continuous signal mentioned above, we adopt discrete Fourier slice theorem, which is a generalization of the discrete Radon transform, to compute refocused image.^[8]

Assume that a lightfield [math]\displaystyle{ \bar{L}_f }[/math] is periodic with periods [math]\displaystyle{ T_s, T_t, T_u, T_v }[/math] and is defined on the hypercube [math]\displaystyle{ H=[-T_s/2,T_s/2]\times[-T_t/2,T_t/2]\times[-T_u/2,T_u/2]\times[-T_v/2,T_v/2] }[/math]. Also, assume there are [math]\displaystyle{ N_s\times N_t\times N_u\times N_v }[/math] known samples of the light field [math]\displaystyle{ (\hat{s}\Delta s, \hat{t}\Delta t, \hat{u}\Delta u, \hat{v}\Delta v) }[/math], where [math]\displaystyle{ \hat{s},\hat{t},\hat{u},\hat{v}\in \mathbb{Z} }[/math] and [math]\displaystyle{ \Delta s,\Delta t,\Delta u,\Delta v=\frac{T_s}{N_s},\frac{T_t}{N_t},\frac{T_u}{N_u},\frac{T_v}{N_v} }[/math], respectively. Then, we can define [math]\displaystyle{ \bar{L}^d_f }[/math] using trigonometric interpolation with these sample points:

[math]\displaystyle{ \bar{L}^d_f(\hat{s},\hat{t},\hat{u},\hat{v})=\sum_{\omega_\hat{s}}\sum_{\omega_\hat{t}}\sum_{\omega_\hat{u}}\sum_{\omega_\hat{v}}\mathcal{\bar{L}}^d_f(\omega_\hat{s},\omega_\hat{t},\omega_\hat{u},\omega_\hat{v})e^{2\pi i(\hat{s}\omega_\hat{s}+\hat{t}\omega_\hat{t}+\hat{u}\omega_\hat{u}+\hat{v}\omega_\hat{v})} }[/math],

where

[math]\displaystyle{ \mathcal{\bar{L}}^d_f(\omega_\hat{s},\omega_\hat{t},\omega_\hat{u},\omega_\hat{v})=\sum_{\hat{s}} \sum_{\hat{t}} \sum_{\hat{u}} \sum_{\hat{v}} \bar{L}^d_f(\hat{s},\hat{t},\hat{u},\hat{v})e^{2\pi i(\hat{s}\omega_\hat{s}+\hat{t}\omega_\hat{t}+\hat{u}\omega_\hat{u}+\hat{v}\omega_\hat{v})} }[/math].

Note that the constant factors are dropped for simplicity.

To compute its refocused photograph, we replace infinite integral in the formula of [math]\displaystyle{ \mathcal{P}_\alpha }[/math] with summation whose bounds are [math]\displaystyle{ [-T_u/2,T_u/2] }[/math] and [math]\displaystyle{ [-T_v/2,T_v/2] }[/math]. That is,

[math]\displaystyle{ \mathcal{P}^d_\alpha[\bar{L^d_f}](\hat{s},\hat{t})={1 \over \alpha^2 f^2}\sum^{N_u/2}_{-N_u/2}\sum^{N_v/2}_{-N_v/2}\bar{L}^d_f(\hat{u}\Delta u(1-1/\alpha)+\hat{s}\Delta s/\alpha,\hat{v}\Delta v(1-1/\alpha)+\hat{t}\Delta t/\alpha,\hat{u}\Delta u,\hat{v}\Delta v) }[/math].

Then, by discrete Fourier slice theorem indicates, we can represent the photograph using Fourier slice:

[math]\displaystyle{ \mathcal{P}^d_\alpha[\bar{L^d_f}](\hat{s},\hat{t})=\sum^{N_u/2}_{-N_u/2}\sum^{N_v/2}_{-N_v/2} {e^{2\pi i(\hat{s}\omega_\hat{s}+\hat{t}\omega_\hat{t})}\mathcal{\bar{L}}^d_f} {(\alpha\omega_\hat{s},\alpha\omega_\hat{t},(1-\alpha)\omega_\hat{s},(1-\alpha)\omega_{\hat{t}})} }[/math]

Realization from the wave optics picture

Although ray-optics based plenoptic camera has demonstrated favorable performance in the macroscopic world, diffraction places a limit on the LFM reconstruction when staying with ray-optics parlance. Hence, it may be much more convenient to switch to wave optics. (This section mainly introduce the work of Broxton et al., 2013.^[2])

Discretization of the space

The interested FOV is segmented into [math]\displaystyle{ N_v }[/math] voxels, each with a label [math]\displaystyle{ i }[/math]. Thus, the whole FOV can be discretely represented with a vector [math]\displaystyle{ \mathbf{g} }[/math] with a dimension of [math]\displaystyle{ N_v\times1 }[/math]. Similarly, a [math]\displaystyle{ N_p\times1 }[/math] vector [math]\displaystyle{ \mathbf{f} }[/math] represents the sensor plane, where each element [math]\displaystyle{ \mathrm{f}_j }[/math] denotes one sensor pixel. Under the condition of incoherent propagation among different voxels, the light field transmission from the object space to the sensor can be linearly linked by a [math]\displaystyle{ N_p\times N_v }[/math] measurement matrix, in which the information of PSF is incorporated:

[math]\displaystyle{ \mathbf{f}=\mathrm{H}~\mathbf{g}. }[/math]

In the ray-optics scenario, a focal stack is generated via synthetically focusing of rays, and then deconvolution with a synthesized PSF is applied to diminish the blurring caused by the wave nature of light. In the wave optics picture, on the other hand, the measurement matrix [math]\displaystyle{ \mathrm{H} }[/math]–describing light field transmission–is directly calculated based on propagation of waves. Unlike transitional optical microscopes whose PSF shape is invariant (e.g., Airy Pattern) with respect to position of the emitter, an emitter in each voxel generates a unique pattern on the sensor of a LFM. In other words, each column in [math]\displaystyle{ \mathrm{H} }[/math] is distinct. In the following sections, the calculation of the whole measurement matrix would be discussed in detail.

Optical impulse response

The optical impulse response [math]\displaystyle{ h(\mathbf{x},\mathbf{p}) }[/math] is the intensity of an electric field at a 2D position [math]\displaystyle{ \mathbf{x}\in\mathbb{R^2} }[/math] on the sensor plane when an isotropic point source of unit amplitude is placed at some 3D position [math]\displaystyle{ \mathbf{p}\in\mathbb{R^3} }[/math] in the FOV. There are three steps along the electric-field propagation: traveling from a point source to the native image plane (i.e., the microlens array plane), passing through the microlens array, and propagating onto the sensor plane.

Step 1: Propagation cross an objective

For an objective with a circular aperture, the wavefront at the native image plane [math]\displaystyle{ \mathbf{x}=(x_1,x_2) }[/math] initiated from an emitter at [math]\displaystyle{ \mathbf{p}=(p_1,p_2,p_3) }[/math] can be computed using the scalar Debye theory:^[9]

[math]\displaystyle{ U_i(\mathbf{x},\mathbf{p})=\frac{\mathrm{M}}{f_{obj}^2\lambda^2}\exp\biggl(-\frac{iu}{4\sin^2(\alpha/2)}\biggr)\int_{0}^{\alpha}d\theta~P(\theta)\exp\biggl(-\frac{iu\sin^2(\theta/2)}{2\sin^2(\alpha/2)}\biggr)J_0\biggl(\frac{\sin\theta}{\sin\alpha}\nu\biggr)\sin\theta }[/math],

where [math]\displaystyle{ f_{obj} }[/math] is the focal length of the objective; [math]\displaystyle{ \mathrm{M} }[/math] is its magnification. [math]\displaystyle{ \lambda }[/math] is the wavelength. [math]\displaystyle{ \alpha=\arcsin(\mathrm{NA}/n) }[/math] is the half-angle of the numerical aperture ([math]\displaystyle{ n }[/math] is the index of refraction of the sample). [math]\displaystyle{ P(\theta) }[/math] is the apodization function of the microscope ([math]\displaystyle{ P(\theta)=\sqrt{\cos\theta} }[/math] for Abbe-sine corrected objectives). [math]\displaystyle{ J_0(\cdot) }[/math] is the zeroth order Bessel function of the first kind. [math]\displaystyle{ \nu }[/math] and [math]\displaystyle{ u }[/math] are the normalized radial and axial optical coordinates, respectively:

[math]\displaystyle{ \nu\thickapprox k\sqrt{(x_1-p_1)^2+(x_2-p_2)^2}\sin\alpha }[/math]

[math]\displaystyle{ u\thickapprox 4 k p_3\sin^2(\alpha/2) }[/math],

where [math]\displaystyle{ k=2\pi n/\lambda }[/math] is the wave number.

Step 2: Focusing through the microlens array

Each microlens can be regarded as a phase mask:

[math]\displaystyle{ \phi(\mathbf x)=\exp\biggl(\frac{-ik}{2f}\|\Delta\mathbf x\|_2^2\biggr) }[/math],

where [math]\displaystyle{ f }[/math] is the focal length of microlenses and [math]\displaystyle{ \Delta\mathbf x=\mathbf x-\mathbf x_{\mu lens} }[/math] is the vector pointing from the center of the microlens to a point [math]\displaystyle{ \mathbf x }[/math] on the microlens. It is worth noticing that [math]\displaystyle{ \phi(\mathbf x) }[/math] is non-zero only when [math]\displaystyle{ \mathbf x }[/math] is located at the effective transmission area of a microlens.

Thereby, the transmission function of the overall microlens array can be represented as [math]\displaystyle{ \phi(\mathbf x) }[/math] convoluted with a 2D comb function:

[math]\displaystyle{ \Phi(\mathbf x)=\phi (\mathbf x)*\mathrm{comb}(\mathbf x/d) }[/math],

where [math]\displaystyle{ d }[/math] is the pitch (say, the dimension) of microlenses.

Step 3: Near-field propagation to the sensor

The propagation of wave front with distance [math]\displaystyle{ f }[/math] from the native image plane to the sensor plane can be computed with a Fresnel diffraction integral:

[math]\displaystyle{ E(\mathbf{x})|_{z=f} = \frac{e^{ikf}}{i \lambda f} \iint E(\mathbf{x}')|_{z=0} \exp\biggl(\frac{ik}{2f}\|\mathbf{x}-\mathbf{x}'\|_2^2\biggr)d\mathbf{x}' }[/math],

where [math]\displaystyle{ E(\mathbf{x}')|_{z=0}=U_i(\mathbf{x}',\mathbf{p})\Phi(\mathbf{x}') }[/math] is the wave front immediately passing the native imaging plane.

Therefore, the whole optical impulse response can be expressed in terms of a convolution:

[math]\displaystyle{ h(\mathbf{x},\mathbf{p})=\biggl(U_i(\mathbf{x},\mathbf{p})\Phi(\mathbf{x})\biggr) * \biggl(\frac{e^{ikf}}{i \lambda f}e^{\frac{ik}{2f}\mathbf \|\mathbf x\|_2^2}\biggr) }[/math].

Computing the measurement matrix

Having acquired the optical impulse response, any element [math]\displaystyle{ h_{ij} }[/math] in the measurement matrix [math]\displaystyle{ \mathrm{H} }[/math] can be calculated as:

[math]\displaystyle{ h_{ij}=\int_{\alpha_j} \int_{\beta_i} w_i(\mathbf{p})|h(\mathbf{x},\mathbf{p})|^2 d\mathbf{p}d\mathbf{x} }[/math],

where [math]\displaystyle{ \alpha_j }[/math] is the area for pixel [math]\displaystyle{ j }[/math] and [math]\displaystyle{ \beta_i }[/math] is the volume for voxel [math]\displaystyle{ i }[/math]. The weight filter [math]\displaystyle{ w_i(\mathbf{p}) }[/math] is added to match the fact that a PSF contributes more at the center of a voxel than at the edges. The linear superposition integral is based on the assumption that fluorophores in each infinitesimal volume [math]\displaystyle{ d\mathbf{p} }[/math] experience an incoherent, stochastic emission process, considering their rapid, random fluctuations.

Solving the inverse problem

The noisy nature of the measurements

Again, due to the limited bandwidth, the photon shot noise, and the huge matrix dimension, it is impossible to directly solve the inverse problem as: [math]\displaystyle{ \mathbf{g}=\mathrm{H}^{-1}\mathbf{f} }[/math]. Instead, a stochastic relation between a discrete light field and FOV more resembles:

[math]\displaystyle{ \hat{\mathbf {f}}}\sim\mathrm{Pois}(\mathrm {H} ~{\mathbf {g}+\mathbf{b}) }[/math],

where [math]\displaystyle{ \mathbf{b} }[/math] is the background fluorescence measured prior to imaging; [math]\displaystyle{ \mathrm{Pois}(\cdot) }[/math] is the Poisson noise. Therefore, [math]\displaystyle{ \hat{\mathbf {f}} }[/math] now becomes a random vector with Possion-distributed values in units of photoelectrons e⁻.

Maximum likelihood estimation

Based on the idea of maximizing the likelihood of the measured light field [math]\displaystyle{ \hat{\mathbf {f}} }[/math] given a particular FOV [math]\displaystyle{ \mathbf {g} }[/math] and background [math]\displaystyle{ \mathbf {b} }[/math], the Richardson-Lucy iteration scheme provides an effective 3D deconvolution algorithm here:

[math]\displaystyle{ \mathbf{g}^{(k+1)}=\mathrm{diag}(\mathrm{H}^T\mathbf{1})^{-1}\mathrm{diag}(\mathrm{H}^T\mathrm{diag}(\mathrm{H}\mathbf{g}^{(k)}+\mathbf{b})^{-1}\mathbf{f})\mathbf{g}^{(k)} }[/math].

where the operator [math]\displaystyle{ \mathrm{diag}(\cdot) }[/math] remains the diagonal arguments of a matrix and sets its off-diagonal elements to zero.

Applications

Light Field Microscopy for functional neural imaging

Starting with initial work at Stanford University applying Light Field Microscopy to calcium imaging in larval zebrafish (Danio Rerio),^[10] a number of articles have now applied Light Field Microscopy to functional neural imaging including measuring the neuron dynamic activities across the whole brain of C. elegans,^[11] whole-brain imaging in larval zebrafish,^[11][12] imaging calcium and voltage activity sensors across the brain of fruit flies (Drosophila) at up to 200 Hz,^[13] and fast imaging of 1mm x 1mm x 0.75mm volumes in the hippocampus of mice navigating a virtual environment.^[14] This area of application is a rapidly developing area at the intersection of computational optics and neuroscience.^[15]

See also

• Light field
• Microlens
• Tomography
• Aperture synthesis
• Voxel

References

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Light field microscopy. Read more