Magnetic flux

Magnetic flux
Common symbols	Φ, ΦB
SI unit	weber (Wb)
Other units	maxwell
In SI base units	kg⋅m2⋅s−2⋅A−1
Dimension	M L2 T−2 I−1

Short description: Surface integral of the magnetic field

In physics, specifically electromagnetism, the magnetic flux through a surface is the surface integral of the normal component of the magnetic field B over that surface. It is usually denoted $Φ$ or $Φ B$ . The SI unit of magnetic flux is the weber (Wb; in derived units, volt–seconds), and the CGS unit is the maxwell. Magnetic flux is usually measured with a fluxmeter, which contains measuring coils, and it calculates the magnetic flux from the change of voltage on the coils.

Description

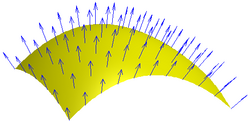
The magnetic flux through a surface—when the magnetic field is variable—relies on splitting the surface into small surface elements, over which the magnetic field can be considered to be locally constant. The total flux is then a formal summation of these surface elements (see surface integration).

Each point on a surface is associated with a direction, called the surface normal; the magnetic flux through a point is then the component of the magnetic field along this direction.

The magnetic interaction is described in terms of a vector field, where each point in space is associated with a vector that determines what force a moving charge would experience at that point (see Lorentz force).^[1] Since a vector field is quite difficult to visualize, introductory physics instruction often uses field lines to visualize this field. The magnetic flux through some surface, in this simplified picture, is proportional to the number of field lines passing through that surface (in some contexts, the flux may be defined to be precisely the number of field lines passing through that surface; although technically misleading, this distinction is not important). The magnetic flux is the net number of field lines passing through that surface; that is, the number passing through in one direction minus the number passing through in the other direction (see below for deciding in which direction the field lines carry a positive sign and in which they carry a negative sign).^[2] More sophisticated physical models drop the field line analogy and define magnetic flux as the surface integral of the normal component of the magnetic field passing through a surface. If the magnetic field is constant, the magnetic flux passing through a surface of vector area S is [math]\displaystyle{ \Phi_B = \mathbf{B} \cdot \mathbf{S} = BS \cos \theta, }[/math] where B is the magnitude of the magnetic field (the magnetic flux density) having the unit of Wb/m² (tesla), S is the area of the surface, and θ is the angle between the magnetic field lines and the normal (perpendicular) to S. For a varying magnetic field, we first consider the magnetic flux through an infinitesimal area element dS, where we may consider the field to be constant: [math]\displaystyle{ d\Phi_B = \mathbf{B} \cdot d\mathbf{S}. }[/math] A generic surface, S, can then be broken into infinitesimal elements and the total magnetic flux through the surface is then the surface integral [math]\displaystyle{ \Phi_B = \iint_S \mathbf{B} \cdot d\mathbf S. }[/math] From the definition of the magnetic vector potential A and the fundamental theorem of the curl the magnetic flux may also be defined as: [math]\displaystyle{ \Phi_B = \oint_{\partial S} \mathbf{A} \cdot d\boldsymbol{\ell}, }[/math] where the line integral is taken over the boundary of the surface $S$ , which is denoted $\partial S$ .

Magnetic flux through a closed surface

Some examples of closed surfaces (left) and open surfaces (right). Left: Surface of a sphere, surface of a torus, surface of a cube. Right: Disk surface, square surface, surface of a hemisphere. (The surface is blue, the boundary is red.)

Main page: Physics:Gauss's law for magnetism

Gauss's law for magnetism, which is one of the four Maxwell's equations, states that the total magnetic flux through a closed surface is equal to zero. (A "closed surface" is a surface that completely encloses a volume(s) with no holes.) This law is a consequence of the empirical observation that magnetic monopoles have never been found.

In other words, Gauss's law for magnetism is the statement:

[math]\displaystyle{ \Phi_B=\,\! }[/math] $\oiint$ [math]\displaystyle{ \scriptstyle S }[/math] [math]\displaystyle{ \mathbf{B} \cdot d\mathbf S = 0 }[/math]

for any closed surface S.

Magnetic flux through an open surface

For an open surface Σ, the electromotive force along the surface boundary, ∂Σ, is a combination of the boundary's motion, with velocity v, through a magnetic field B (illustrated by the generic F field in the diagram) and the induced electric field caused by the changing magnetic field.

While the magnetic flux through a closed surface is always zero, the magnetic flux through an open surface need not be zero and is an important quantity in electromagnetism.

When determining the total magnetic flux through a surface only the boundary of the surface needs to be defined, the actual shape of the surface is irrelevant and the integral over any surface sharing the same boundary will be equal. This is a direct consequence of the closed surface flux being zero.

Changing magnetic flux

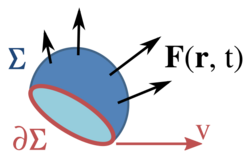
Main page: Physics:Faraday's law of induction

For example, a change in the magnetic flux passing through a loop of conductive wire will cause an electromotive force, and therefore an electric current, in the loop. The relationship is given by Faraday's law: [math]\displaystyle{ \mathcal{E} = \oint_{\partial \Sigma} \left( \mathbf{E} + \mathbf v \times \mathbf B\right) \cdot d\boldsymbol{\ell} = -\frac{d\Phi_B}{dt}, }[/math] where

[math]\displaystyle{ \mathcal{E} }[/math] is the electromotive force (EMF),
the minus-sign represents Lenz's Law,
$Φ B$ is the magnetic flux through the open surface $Σ$ ,
$\partialΣ$ is the boundary of the open surface $Σ$ ; the surface, in general, may be in motion and deforming, and so is generally a function of time. The electromotive force is induced along this boundary.
$d ℓ$ is an infinitesimal vector element of the contour $\partialΣ$ ,
$v$ is the velocity of the boundary $\partialΣ$ ,
$E$ is the electric field,
$B$ is the magnetic field.

The two equations for the EMF are, firstly, the work per unit charge done against the Lorentz force in moving a test charge around the (possibly moving) surface boundary $\partialΣ$ and, secondly, as the change of magnetic flux through the open surface $Σ$ . This equation is the principle behind an electrical generator.

Area defined by an electric coil with three turns.

Comparison with electric flux

Main pages: Physics:Electric flux and Physics:Gauss's law

By way of contrast, Gauss's law for electric fields, another of Maxwell's equations, is

[math]\displaystyle{ \Phi_E =\,\! }[/math] $\oiint$ [math]\displaystyle{ \scriptstyle S }[/math] [math]\displaystyle{ \mathbf{E}\cdot d\mathbf{S} = \frac{Q}{\varepsilon_0}\,\! }[/math]

where

E is the electric field,
S is any closed surface,
Q is the total electric charge inside the surface S,
ε₀ is the electric constant (a universal constant, also called the "permittivity of free space").

The flux of E through a closed surface is not always zero; this indicates the presence of "electric monopoles", that is, free positive or negative charges.

References

↑ Purcell, Edward; Morin, David (2013). Electricity and Magnetism (3rd ed.). New York: Cambridge University Press. p. 278. ISBN 978-1-107-01402-2.
↑ Browne, Michael (2008). Physics for Engineering and Science (2nd ed.). McGraw-Hill/Schaum. p. 235. ISBN 978-0-07-161399-6.

External articles

Vicci, "Magnetic-flux conduits", US patent 6720855, issued 2003
Magnetic Flux through a Loop of Wire by Ernest Lee, Wolfram Demonstrations Project.
Conversion Magnetic flux Φ in nWb per meter track width to flux level in dB – Tape Operating Levels and Tape Alignment Levels
wikt:magnetic flux

0.00

(0 votes)

Original source: https://en.wikipedia.org/wiki/Magnetic flux. Read more

[1] Purcell, Edward; Morin, David (2013). Electricity and Magnetism (3rd ed.). New York: Cambridge University Press. p. 278. ISBN 978-1-107-01402-2.

[2] Browne, Michael (2008). Physics for Engineering and Science (2nd ed.). McGraw-Hill/Schaum. p. 235. ISBN 978-0-07-161399-6.

[1]

[2]