Offshore crane shock absorber
Topic: Physics
 From HandWiki - Reading time: 4 min
From HandWiki - Reading time: 4 min
An offshore crane shock absorber is a gas spring with hydraulic damping used to reduce dynamic loads during offshore lifting. The lifting capacity of the offshore crane can be increased significantly during lifting in high sea states if a shock absorber is fitted. [1]
Crane design load
Offshore lifting capacity is governed by classification society rules. The fundamental rule is that the design load should not be exceeded. The design load is given by:
[math]\displaystyle{ F_m= \psi m_s g }[/math]
Where:
[math]\displaystyle{ F_m }[/math] - Crane design load
[math]\displaystyle{ \psi }[/math] - Dynamic coefficient
[math]\displaystyle{ m_s }[/math] - Safe working load
[math]\displaystyle{ g }[/math] - Acceleration of gravity
The classification societies require that [math]\displaystyle{ \psi }[/math] ≥1.3 for offshore cranes. This means that [math]\displaystyle{ m_s }[/math] cannot exceed [math]\displaystyle{ \frac {F_m}{\psi g} }[/math] even for platform lifts.[2][3][4]
Dynamic load
To calculate the dynamic load the classification societies use energy equations. The kinetic energy of the load is expressed as:
[math]\displaystyle{ E_k=\frac {1}{2} m_s v_r^2 }[/math]
Where:
[math]\displaystyle{ E_k }[/math] - Kinetic energy of the load
[math]\displaystyle{ v_r }[/math] - Relative velocity between crane hook and load
Energy absorbed by the crane is given by:
[math]\displaystyle{ E_c=\frac {1}{2} k y^2 }[/math]
Where:
[math]\displaystyle{ E_c }[/math] - Spring energy stored in crane structure
[math]\displaystyle{ k }[/math] - Stiffness of offshore crane
[math]\displaystyle{ y }[/math] - Vertical displacement of crane hook
The spring force is given by:
[math]\displaystyle{ F_c=ky }[/math]
Combining the two previous equations yields an alternative description of the energy stored in the crane structure:
[math]\displaystyle{ E_c=\frac {1}{2}k (\frac {F_c}{k})^2=\frac {F_c^2}{2k} }[/math]
During an offshore lift the crane does not start to absorb energy from the load before the force in the crane wire exceeds the static weight of the load, which means that we can write the energy absorption of the crane as:
[math]\displaystyle{ E_c=\frac {(m_s \psi g-m_s g)^2}{2k} }[/math]
Setting [math]\displaystyle{ E_c }[/math] equal to [math]\displaystyle{ E_k }[/math]:
[math]\displaystyle{ \frac {(m_s \psi g-m_s g)^2}{2k}=\frac {1}{2} m_s v_r^2 }[/math]
And solving for [math]\displaystyle{ \psi }[/math]:
[math]\displaystyle{ \psi= 1+\frac {v_r}{g}\sqrt{\frac {k}{m}} }[/math]
The dynamic factor will always be larger than 1 because there will always be a velocity difference between the crane hook and the load during offshore lifts. The value of [math]\displaystyle{ \psi }[/math] determines the lifting capacity as a function of [math]\displaystyle{ v_r }[/math] which is dependent on the significant wave height.
If the offshore crane has a shock absorber mounted it will absorb energy according to:
[math]\displaystyle{ E_a=\eta \mu S m_s g (\psi -1) }[/math]
Where:
[math]\displaystyle{ E_a }[/math] - Energy absorbed by shock absorber
[math]\displaystyle{ \mu }[/math] - Stroke utilization (safety factor), standard value 0.9
[math]\displaystyle{ \eta }[/math] - Efficiency of shock absorber, usually possible to get close to 0.9
[math]\displaystyle{ S }[/math] - Stroke length
Adding this to the energy balance yields:
[math]\displaystyle{ \frac {(m_s \psi g-m_s g)^2}{2k}+\eta \mu S m_s g (\psi -1)=\frac {1}{2} m_s v_r^2 }[/math]
Again solving for ψ:
[math]\displaystyle{ \psi=1+ \frac {\sqrt{(\mu \eta S k)^2+m_s k v_r^2}-\mu \eta S k} {m_s g} }[/math]
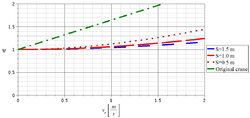
The plot to the right shows the effect of the shock absorber stroke length.
Estimating relative velocity
The relative velocity is defined by several classification societies as:
[math]\displaystyle{ v_r=\frac {1} {2} v_L + \sqrt{v_d^2 + v_c^2} }[/math]
Where:
[math]\displaystyle{ v_L }[/math] - Maximum crane lifting velocity at this SWL
[math]\displaystyle{ v_d }[/math] - Vertical velocity of the deck which the load is placed on
[math]\displaystyle{ v_c }[/math] - Vertical velocity of the crane tip due to wave motion
[math]\displaystyle{ v_L }[/math] has to be gathered from crane user manual or be measured. The deck velocity can be estimated from Table 1.
| Lifting from or to | [math]\displaystyle{ v_d }[/math] |
|---|---|
| Platform or fixed structure | [math]\displaystyle{ 0 }[/math] |
| Supply boat or barge | [math]\displaystyle{ 0.6 H_s }[/math] if [math]\displaystyle{ H_s }[/math] ≤3 [math]\displaystyle{ 1.8 + 0.3(H_s-3) }[/math] if [math]\displaystyle{ H_s }[/math]>3 |
The crane tip velocity, [math]\displaystyle{ v_c }[/math], can be estimated by Table 2.
| Lifting from or to | [math]\displaystyle{ v_d }[/math] |
|---|---|
| Platform or fixed structure | [math]\displaystyle{ 0 }[/math] |
| Tension leg platform or Spar | [math]\displaystyle{ 0.05 H_s }[/math] |
| Semisubmersible | [math]\displaystyle{ 0.082 H_s^2 }[/math] |
| FPSO or drillship | [math]\displaystyle{ 0.164 H_s^2 }[/math] |
These estimations are conservative and for large ships/rigs they may deviate significantly from reality.
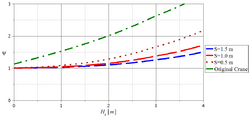
A plot of the dynamic factor versus significant wave height for a crane mounted on a semisubmersible and lifting from supply boat is shown above to the right.
References
- ↑ The Engineers Guide Safelink AS
- ↑ EN13852-1:2004 Cranes - Offshore cranes - Part 1: General - purpose offshore cranes
- ↑ DNV Standard For Certification No. 2.22 Lifting Appliances October 2011
- ↑ API 2C 7th Ed. Specification for Offshore Pedestal-mounted Cranes
 |
 KSF
KSF