Table of Contents Categories
  Encyclosphere.org ENCYCLOREADER
  supported by EncyclosphereKSF

Phase transition

Topic: Physics

 From HandWiki - Reading time: 22 min
Short description: Physical process of transition between basic states of matter
This diagram shows the nomenclature for the different phase transitions.

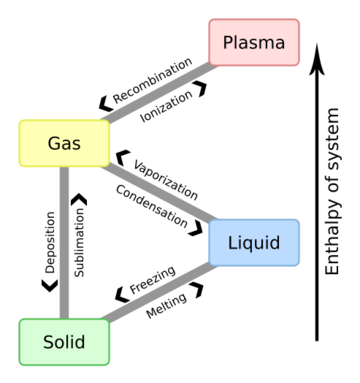
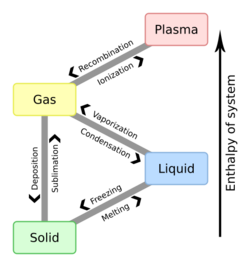
In chemistry, thermodynamics, and other related fields, a phase transition (or phase change) is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic states of matter: solid, liquid, and gas, and in rare cases, plasma. A phase of a thermodynamic system and the states of matter have uniform physical properties. During a phase transition of a given medium, certain properties of the medium change as a result of the change of external conditions, such as temperature or pressure. This can be a discontinuous change; for example, a liquid may become gas upon heating to its boiling point, resulting in an abrupt change in volume. The identification of the external conditions at which a transformation occurs defines the phase transition point.

Types of phase transition

States of matter

A simplified phase diagram for water, showing whether solid ice, liquid water, or gaseous water vapor is the most stable at different combinations of temperature and pressure.

Phase transitions commonly refer to when a substance transforms between one of the four states of matter to another. At the phase transition point for a substance, for instance the boiling point, the two phases involved - liquid and vapor, have identical free energies and therefore are equally likely to exist. Below the boiling point, the liquid is the more stable state of the two, whereas above the boiling point the gaseous form is the more stable.

Common transitions between the solid, liquid, and gaseous phases of a single component, due to the effects of temperature and/or pressure are identified in the following table: Template:Table of Phase Transitions

For a single component, the most stable phase at different temperatures and pressures can be shown on a phase diagram. Such a diagram usually depicts states in equilibrium. A phase transition usually occurs when the pressure or temperature changes and the system crosses from one region to another, like water turning from liquid to solid as soon as the temperature drops below the freezing point. In exception to the usual case, it is sometimes possible to change the state of a system diabatically (as opposed to adiabatically) in such a way that it can be brought past a phase transition point without undergoing a phase transition. The resulting state is metastable, i.e., less stable than the phase to which the transition would have occurred, but not unstable either. This occurs in superheating and supercooling, for example. Metastable states do not appear on usual phase diagrams.

Structural

A phase diagram showing the allotropes of iron, distinguishing between different several different crystal structures including ferrite (α-iron) and austenite (γ-iron).

Phase transitions can also occur when a solid changes to a different structure without changing its chemical makeup. In elements, this is known as allotropy, whereas in compounds it is known as polymorphism. The change from one crystal structure to another, from a crystalline solid to an amorphous solid, or from one amorphous structure to another (polyamorphs) are all examples of solid to solid phase transitions.

The martensitic transformation occurs as one of the many phase transformations in carbon steel and stands as a model for displacive phase transformations. Order-disorder transitions such as in alpha-titanium aluminides. As with states of matter, there are also a metastable to equilibrium phase transformation for structural phase transitions. A metastable polymorph which forms rapidly due to lower surface energy will transform to an equilibrium phase given sufficient thermal input to overcome an energetic barrier.

Magnetic

A phase diagram showing different magnetic structures in the same crystal structure of Manganese monosilicide.

Phase transitions can also describe the change between different kinds of magnetic ordering. The most well-known is the transition between the ferromagnetic and paramagnetic phases of magnetic materials, which occurs at what is called the Curie point. Another example is the transition between differently ordered, commensurate or incommensurate, magnetic structures, such as in cerium antimonide.

Mixtures

A binary phase diagram showing the most stable chemical compounds of titanium and nickel at different mixing ratios and temperatures.

Phase transitions involving solutions and mixtures are more complicated than transitions involving a single compound. While chemically pure compounds exhibit a single temperature melting point between solid and liquid phases, mixtures can either have a single melting point, known as congruent melting, or they have different liquidus and solidus temperatures resulting in a temperature span where solid and liquid coexist in equilibrium. This is often the case in solid solutions, where the two components are isostructural.

There are also a number of phase transitions involving three phases: a eutectic transformation, in which a two-component single-phase liquid is cooled and transforms into two solid phases. The same process, but beginning with a solid instead of a liquid is called a eutectoid transformation. A peritectic transformation, in which a two-component single-phase solid is heated and transforms into a solid phase and a liquid phase. A peritectoid reaction is a peritectoid rection, except involving only solid phases. A monotectic reaction consists of change from a liquid and to a combination of a solid and a second liquid, where the two liquids display a miscibility gap.[1]

Separation into multiple phases can occur via spinodal decomposition, in which a single phase is cooled and separates into two different compositions.

Non-equilibrium mixtures can occur, such as in supersaturation.

Other examples

A small piece of rapidly melting solid argon shows two concurrent phase changes. The transition from solid to liquid, and gas to liquid (shown by the white condensed water vapour).

Other phase changes include:

Phase transitions occur when the thermodynamic free energy of a system is non-analytic for some choice of thermodynamic variables (cf. phases). This condition generally stems from the interactions of a large number of particles in a system, and does not appear in systems that are small. Phase transitions can occur for non-thermodynamic systems, where temperature is not a parameter. Examples include: quantum phase transitions, dynamic phase transitions, and topological (structural) phase transitions. In these types of systems other parameters take the place of temperature. For instance, connection probability replaces temperature for percolating networks.

Condensed matter physics
QuantumPhaseTransition.svg
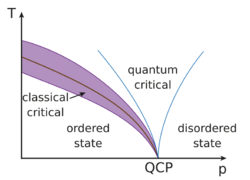Phases · Phase transition · QCP
States of matter
Solid · Liquid · Gas · Plasma · Bose–Einstein condensate · Bose gas · Fermionic condensate · Fermi gas · Fermi liquid · Supersolid · Superfluidity · Luttinger liquid  · Time crystal

Classifications

Ehrenfest classification

Paul Ehrenfest classified phase transitions based on the behavior of the thermodynamic free energy as a function of other thermodynamic variables.[5] Under this scheme, phase transitions were labeled by the lowest derivative of the free energy that is discontinuous at the transition. First-order phase transitions exhibit a discontinuity in the first derivative of the free energy with respect to some thermodynamic variable.[6] The various solid/liquid/gas transitions are classified as first-order transitions because they involve a discontinuous change in density, which is the (inverse of the) first derivative of the free energy with respect to pressure. Second-order phase transitions are continuous in the first derivative (the order parameter, which is the first derivative of the free energy with respect to the external field, is continuous across the transition) but exhibit discontinuity in a second derivative of the free energy.[6] These include the ferromagnetic phase transition in materials such as iron, where the magnetization, which is the first derivative of the free energy with respect to the applied magnetic field strength, increases continuously from zero as the temperature is lowered below the Curie temperature. The magnetic susceptibility, the second derivative of the free energy with the field, changes discontinuously. Under the Ehrenfest classification scheme, there could in principle be third, fourth, and higher-order phase transitions. For example, the Gross–Witten–Wadia phase transition in 2-d lattice quantum chromodynamics is a third-order phase transition.[7][8] The Curie points of many ferromagnetics is also a third-order transition, as shown by their specific heat having a sudden change in slope.[9][10]

The Ehrenfest classification implicitly allows for continuous phase transformations, where the bonding character of a material changes, but there is no discontinuity in any free energy derivative. An example of this occurs at the supercritical liquid–gas boundaries.

The first example of a phase transition which did not fit into the Ehrenfest classification was the exact solution of the Ising model, discovered in 1944 by Lars Onsager. The exact specific heat differed from the earlier mean-field approximations, which had predicted that it has a simple discontinuity at critical temperature. Instead, the exact specific heat had a logarithmic divergence at the critical temperature.[11] In the following decades, the Ehrenfest classification was replaced by a simplified classification scheme that is able to incorporate such transitions.

Modern classifications

In the modern classification scheme, phase transitions are divided into two broad categories, named similarly to the Ehrenfest classes:[5]

First-order phase transitions are those that involve a latent heat. During such a transition, a system either absorbs or releases a fixed (and typically large) amount of energy per volume. During this process, the temperature of the system will stay constant as heat is added: the system is in a "mixed-phase regime" in which some parts of the system have completed the transition and others have not.[12][13]

Familiar examples are the melting of ice or the boiling of water (the water does not instantly turn into vapor, but forms a turbulent mixture of liquid water and vapor bubbles). Yoseph Imry and Michael Wortis showed that quenched disorder can broaden a first-order transition. That is, the transformation is completed over a finite range of temperatures, but phenomena like supercooling and superheating survive and hysteresis is observed on thermal cycling.[14][15][16]

Second-order phase transitions are also called "continuous phase transitions". They are characterized by a divergent susceptibility, an infinite correlation length, and a power law decay of correlations near criticality. Examples of second-order phase transitions are the ferromagnetic transition, superconducting transition (for a Type-I superconductor the phase transition is second-order at zero external field and for a Type-II superconductor the phase transition is second-order for both normal-state–mixed-state and mixed-state–superconducting-state transitions) and the superfluid transition. In contrast to viscosity, thermal expansion and heat capacity of amorphous materials show a relatively sudden change at the glass transition temperature[17] which enables accurate detection using differential scanning calorimetry measurements. Lev Landau gave a phenomenological theory of second-order phase transitions.

Apart from isolated, simple phase transitions, there exist transition lines as well as multicritical points, when varying external parameters like the magnetic field or composition.

Several transitions are known as infinite-order phase transitions. They are continuous but break no symmetries. The most famous example is the Kosterlitz–Thouless transition in the two-dimensional XY model. Many quantum phase transitions, e.g., in two-dimensional electron gases, belong to this class.

The liquid–glass transition is observed in many polymers and other liquids that can be supercooled far below the melting point of the crystalline phase. This is atypical in several respects. It is not a transition between thermodynamic ground states: it is widely believed that the true ground state is always crystalline. Glass is a quenched disorder state, and its entropy, density, and so on, depend on the thermal history. Therefore, the glass transition is primarily a dynamic phenomenon: on cooling a liquid, internal degrees of freedom successively fall out of equilibrium. Some theoretical methods predict an underlying phase transition in the hypothetical limit of infinitely long relaxation times.[18][19] No direct experimental evidence supports the existence of these transitions.

The gelation transition of colloidal particles has been shown to be a second-order phase transition under nonequilibrium conditions.[20]

Characteristic properties

Phase coexistence

A disorder-broadened first-order transition occurs over a finite range of temperatures where the fraction of the low-temperature equilibrium phase grows from zero to one (100%) as the temperature is lowered. This continuous variation of the coexisting fractions with temperature raised interesting possibilities. On cooling, some liquids vitrify into a glass rather than transform to the equilibrium crystal phase. This happens if the cooling rate is faster than a critical cooling rate, and is attributed to the molecular motions becoming so slow that the molecules cannot rearrange into the crystal positions.[21] This slowing down happens below a glass-formation temperature Tg, which may depend on the applied pressure.[17][22] If the first-order freezing transition occurs over a range of temperatures, and Tg falls within this range, then there is an interesting possibility that the transition is arrested when it is partial and incomplete. Extending these ideas to first-order magnetic transitions being arrested at low temperatures, resulted in the observation of incomplete magnetic transitions, with two magnetic phases coexisting, down to the lowest temperature. First reported in the case of a ferromagnetic to anti-ferromagnetic transition,[23] such persistent phase coexistence has now been reported across a variety of first-order magnetic transitions. These include colossal-magnetoresistance manganite materials,[24][25] magnetocaloric materials,[26] magnetic shape memory materials,[27] and other materials.[28] The interesting feature of these observations of Tg falling within the temperature range over which the transition occurs is that the first-order magnetic transition is influenced by magnetic field, just like the structural transition is influenced by pressure. The relative ease with which magnetic fields can be controlled, in contrast to pressure, raises the possibility that one can study the interplay between Tg and Tc in an exhaustive way. Phase coexistence across first-order magnetic transitions will then enable the resolution of outstanding issues in understanding glasses.

Critical points

In any system containing liquid and gaseous phases, there exists a special combination of pressure and temperature, known as the critical point, at which the transition between liquid and gas becomes a second-order transition. Near the critical point, the fluid is sufficiently hot and compressed that the distinction between the liquid and gaseous phases is almost non-existent. This is associated with the phenomenon of critical opalescence, a milky appearance of the liquid due to density fluctuations at all possible wavelengths (including those of visible light).

Symmetry

Phase transitions often involve a symmetry breaking process. For instance, the cooling of a fluid into a crystalline solid breaks continuous translation symmetry: each point in the fluid has the same properties, but each point in a crystal does not have the same properties (unless the points are chosen from the lattice points of the crystal lattice). Typically, the high-temperature phase contains more symmetries than the low-temperature phase due to spontaneous symmetry breaking, with the exception of certain accidental symmetries (e.g. the formation of heavy virtual particles, which only occurs at low temperatures).[29]

Order parameters

An order parameter is a measure of the degree of order across the boundaries in a phase transition system; it normally ranges between zero in one phase (usually above the critical point) and nonzero in the other.[30] At the critical point, the order parameter susceptibility will usually diverge.

An example of an order parameter is the net magnetization in a ferromagnetic system undergoing a phase transition. For liquid/gas transitions, the order parameter is the difference of the densities.

From a theoretical perspective, order parameters arise from symmetry breaking. When this happens, one needs to introduce one or more extra variables to describe the state of the system. For example, in the ferromagnetic phase, one must provide the net magnetization, whose direction was spontaneously chosen when the system cooled below the Curie point. However, note that order parameters can also be defined for non-symmetry-breaking transitions.[citation needed]

Some phase transitions, such as superconducting and ferromagnetic, can have order parameters for more than one degree of freedom. In such phases, the order parameter may take the form of a complex number, a vector, or even a tensor, the magnitude of which goes to zero at the phase transition.[citation needed]

There also exist dual descriptions of phase transitions in terms of disorder parameters. These indicate the presence of line-like excitations such as vortex- or defect lines.

Relevance in cosmology

Symmetry-breaking phase transitions play an important role in cosmology. As the universe expanded and cooled, the vacuum underwent a series of symmetry-breaking phase transitions. For example, the electroweak transition broke the SU(2)×U(1) symmetry of the electroweak field into the U(1) symmetry of the present-day electromagnetic field. This transition is important to explain the asymmetry between the amount of matter and antimatter in the present-day universe, according to electroweak baryogenesis theory.

Progressive phase transitions in an expanding universe are implicated in the development of order in the universe, as is illustrated by the work of Eric Chaisson[31] and David Layzer.[32]

See also relational order theories and order and disorder.

Critical exponents and universality classes

Main page: Physics:Critical exponent

Continuous phase transitions are easier to study than first-order transitions due to the absence of latent heat, and they have been discovered to have many interesting properties. The phenomena associated with continuous phase transitions are called critical phenomena, due to their association with critical points.

Continuous phase transitions can be characterized by parameters known as critical exponents. The most important one is perhaps the exponent describing the divergence of the thermal correlation length by approaching the transition. For instance, let us examine the behavior of the heat capacity near such a transition. We vary the temperature T of the system while keeping all the other thermodynamic variables fixed and find that the transition occurs at some critical temperature Tc. When T is near Tc, the heat capacity C typically has a power law behavior:

[math]\displaystyle{ C \propto |T_\text{c} - T|^{-\alpha}. }[/math]

The heat capacity of amorphous materials has such a behaviour near the glass transition temperature where the universal critical exponent α = 0.59[33] A similar behavior, but with the exponent ν instead of α, applies for the correlation length.

The exponent ν is positive. This is different with α. Its actual value depends on the type of phase transition we are considering.

The critical exponents are not necessarily the same above and below the critical temperature. When a continuous symmetry is explicitly broken down to a discrete symmetry by irrelevant (in the renormalization group sense) anisotropies, then some exponents (such as [math]\displaystyle{ \gamma }[/math], the exponent of the susceptibility) are not identical.[34]

For −1 < α < 0, the heat capacity has a "kink" at the transition temperature. This is the behavior of liquid helium at the lambda transition from a normal state to the superfluid state, for which experiments have found α = −0.013 ± 0.003. At least one experiment was performed in the zero-gravity conditions of an orbiting satellite to minimize pressure differences in the sample.[35] This experimental value of α agrees with theoretical predictions based on variational perturbation theory.[36]

For 0 < α < 1, the heat capacity diverges at the transition temperature (though, since α < 1, the enthalpy stays finite). An example of such behavior is the 3D ferromagnetic phase transition. In the three-dimensional Ising model for uniaxial magnets, detailed theoretical studies have yielded the exponent α ≈ +0.110.

Some model systems do not obey a power-law behavior. For example, mean field theory predicts a finite discontinuity of the heat capacity at the transition temperature, and the two-dimensional Ising model has a logarithmic divergence. However, these systems are limiting cases and an exception to the rule. Real phase transitions exhibit power-law behavior.

Several other critical exponents, β, γ, δ, ν, and η, are defined, examining the power law behavior of a measurable physical quantity near the phase transition. Exponents are related by scaling relations, such as

[math]\displaystyle{ \beta = \gamma / (\delta - 1),\quad \nu = \gamma / (2 - \eta). }[/math]

It can be shown that there are only two independent exponents, e.g. ν and η.

It is a remarkable fact that phase transitions arising in different systems often possess the same set of critical exponents. This phenomenon is known as universality. For example, the critical exponents at the liquid–gas critical point have been found to be independent of the chemical composition of the fluid.

More impressively, but understandably from above, they are an exact match for the critical exponents of the ferromagnetic phase transition in uniaxial magnets. Such systems are said to be in the same universality class. Universality is a prediction of the renormalization group theory of phase transitions, which states that the thermodynamic properties of a system near a phase transition depend only on a small number of features, such as dimensionality and symmetry, and are insensitive to the underlying microscopic properties of the system. Again, the divergence of the correlation length is the essential point.

Critical phenomena

There are also other critical phenomena; e.g., besides static functions there is also critical dynamics. As a consequence, at a phase transition one may observe critical slowing down or speeding up. Connected to the previous phenomenon is also the phenomenon of enhanced fluctuations before the phase transition, as a consequence of lower degree of stability of the initial phase of the system. The large static universality classes of a continuous phase transition split into smaller dynamic universality classes. In addition to the critical exponents, there are also universal relations for certain static or dynamic functions of the magnetic fields and temperature differences from the critical value.[citation needed]

Phase transitions in biological systems

Phase transitions play many important roles in biological systems. Examples include the lipid bilayer formation, the coil-globule transition in the process of protein folding and DNA melting, liquid crystal-like transitions in the process of DNA condensation, and cooperative ligand binding to DNA and proteins with the character of phase transition.[37]

In biological membranes, gel to liquid crystalline phase transitions play a critical role in physiological functioning of biomembranes. In gel phase, due to low fluidity of membrane lipid fatty-acyl chains, membrane proteins have restricted movement and thus are restrained in exercise of their physiological role. Plants depend critically on photosynthesis by chloroplast thylakoid membranes which are exposed cold environmental temperatures. Thylakoid membranes retain innate fluidity even at relatively low temperatures because of high degree of fatty-acyl disorder allowed by their high content of linolenic acid, 18-carbon chain with 3-double bonds.[38] Gel-to-liquid crystalline phase transition temperature of biological membranes can be determined by many techniques including calorimetry, fluorescence, spin label electron paramagnetic resonance and NMR by recording measurements of the concerned parameter by at series of sample temperatures. A simple method for its determination from 13-C NMR line intensities has also been proposed.[39]

It has been proposed that some biological systems might lie near critical points. Examples include neural networks in the salamander retina,[40] bird flocks[41] gene expression networks in Drosophila,[42] and protein folding.[43] However, it is not clear whether or not alternative reasons could explain some of the phenomena supporting arguments for criticality.[44] It has also been suggested that biological organisms share two key properties of phase transitions: the change of macroscopic behavior and the coherence of a system at a critical point.[45] Phase transitions are prominent feature of motor behavior in biological systems.[46] Spontaneous gait transitions,[47] as well as fatigue-induced motor task disengagements,[48] show typical critical behavior as an intimation of the sudden qualitative change of the previously stable motor behavioral pattern.

The characteristic feature of second order phase transitions is the appearance of fractals in some scale-free properties. It has long been known that protein globules are shaped by interactions with water. There are 20 amino acids that form side groups on protein peptide chains range from hydrophilic to hydrophobic, causing the former to lie near the globular surface, while the latter lie closer to the globular center. Twenty fractals were discovered in solvent associated surface areas of > 5000 protein segments.[49] The existence of these fractals proves that proteins function near critical points of second-order phase transitions.

In groups of organisms in stress (when approaching critical transitions), correlations tend to increase, while at the same time, fluctuations also increase. This effect is supported by many experiments and observations of groups of people, mice, trees, and grassy plants.[50]

Experimental

A variety of methods are applied for studying the various effects. Selected examples are:

  • Thermogravimetry (very common)
  • X-ray diffraction
  • Neutron diffraction
  • Raman Spectroscopy
  • SQUID (measurement of magnetic transitions)
  • Hall effect (measurement of magnetic transitions)
  • Mössbauer spectroscopy (simultaneous measurement of magnetic and non-magnetic transitions. Limited up to about 800–1000 °C)
  • Perturbed angular correlation (simultaneous measurement of magnetic and non-magnetic transitions. No temperature limits. Over 2000 °C already performed, theoretical possible up to the highest crystal material, such as tantalum hafnium carbide 4215 °C.)

See also


References

  1. ↑ Askeland, Donald R.; Haddleton, Frank; Green, Phil; Robertson, Howard (1996). The Science and Engineering of Materials. Chapman & Hall. p. 286. ISBN 978-0-412-53910-7. 
  2. ↑ Rybin, M.V. (2015). "Phase diagram for the transition from photonic crystals to dielectric metamaterials". Nature Communications 6: 10102. doi:10.1038/ncomms10102. PMID 26626302. Bibcode: 2015NatCo...610102R. 
  3. ↑ Eds. Zhou, W., and Fan. S., Semiconductors and Semimetals. Vol 100. Photonic Crystal Metasurface Optoelectronics, Elsevier, 2019
  4. ↑ "Fundamentals of Stable Isotope Geochemistry". USGS. 2004. http://wwwrcamnl.wr.usgs.gov/isoig/res/funda.html. 
  5. ↑ 5.0 5.1 Jaeger, Gregg (1 May 1998). "The Ehrenfest Classification of Phase Transitions: Introduction and Evolution". Archive for History of Exact Sciences 53 (1): 51–81. doi:10.1007/s004070050021. 
  6. ↑ 6.0 6.1 Blundell, Stephen J.; Katherine M. Blundell (2008). Concepts in Thermal Physics. Oxford University Press. ISBN 978-0-19-856770-7. 
  7. ↑ Gross, David J. (1980), Possible third-order phase transition in the large N lattice gauge theory, doi:10.1103/PhysRevD.21.446 
  8. ↑ Majumdar, Satya N; Schehr, Grégory (2014-01-31). "Top eigenvalue of a random matrix: large deviations and third order phase transition". Journal of Statistical Mechanics: Theory and Experiment 2014 (1): P01012. doi:10.1088/1742-5468/2014/01/P01012. ISSN 1742-5468. Bibcode: 2014JSMTE..01..012M. https://iopscience.iop.org/article/10.1088/1742-5468/2014/01/P01012. 
  9. ↑ Pippard, Alfred B. (1981). Elements of classical thermodynamics: for advanced students of physics (Repr ed.). Cambridge: Univ. Pr. pp. 140–141. ISBN 978-0-521-09101-5. 
  10. ↑ Austin, J. B. (November 1932). "Heat Capacity of Iron - A Review". Industrial & Engineering Chemistry 24 (11): 1225–1235. doi:10.1021/ie50275a006. ISSN 0019-7866. 
  11. ↑ Stanley, H. Eugene (1971). Introduction to Phase Transitions and Critical Phenomena. Oxford: Clarendon Press. 
  12. ↑ Faghri, A., and Zhang, Y., Transport Phenomena in Multiphase Systems, Elsevier, Burlington, MA, 2006,
  13. ↑ Faghri, A., and Zhang, Y., Fundamentals of Multiphase Heat Transfer and Flow, Springer, New York, NY, 2020
  14. ↑ Imry, Y.; Wortis, M. (1979). "Influence of quenched impurities on first-order phase transitions". Phys. Rev. B 19 (7): 3580–3585. doi:10.1103/physrevb.19.3580. Bibcode: 1979PhRvB..19.3580I. 
  15. ↑ Kumar, Kranti; Pramanik, A. K.; Banerjee, A.; Chaddah, P.; Roy, S. B.; Park, S.; Zhang, C. L.; Cheong, S.-W. (2006). "Relating supercooling and glass-like arrest of kinetics for phase separated systems: DopedCeFe2and(La,Pr,Ca)MnO3". Physical Review B 73 (18): 184435. doi:10.1103/PhysRevB.73.184435. ISSN 1098-0121. Bibcode: 2006PhRvB..73r4435K. 
  16. ↑ Pasquini, G.; Daroca, D. Pérez; Chiliotte, C.; Lozano, G. S.; Bekeris, V. (2008). "Ordered, Disordered, and Coexistent Stable Vortex Lattices inNbSe2Single Crystals". Physical Review Letters 100 (24): 247003. doi:10.1103/PhysRevLett.100.247003. ISSN 0031-9007. PMID 18643617. Bibcode: 2008PhRvL.100x7003P. 
  17. ↑ 17.0 17.1 Ojovan, M.I. (2013). "Ordering and structural changes at the glass-liquid transition". J. Non-Cryst. Solids 382: 79–86. doi:10.1016/j.jnoncrysol.2013.10.016. Bibcode: 2013JNCS..382...79O. 
  18. ↑ Gotze, Wolfgang. "Complex Dynamics of Glass-Forming Liquids: A Mode-Coupling Theory."
  19. ↑ Lubchenko, V. Wolynes; Wolynes, Peter G. (2007). "Theory of Structural Glasses and Supercooled Liquids". Annual Review of Physical Chemistry 58: 235–266. doi:10.1146/annurev.physchem.58.032806.104653. PMID 17067282. Bibcode: 2007ARPC...58..235L. 
  20. ↑ Rouwhorst, J; Ness, C.; Soyanov, S.; Zaccone, A.; Schall, P (2020). "Nonequilibrium continuous phase transition in colloidal gelation with short-range attraction". Nature Communications 11 (1): 3558. doi:10.1038/s41467-020-17353-8. PMID 32678089. Bibcode: 2020NatCo..11.3558R. 
  21. ↑ Greer, A. L. (1995). "Metallic Glasses". Science 267 (5206): 1947–1953. doi:10.1126/science.267.5206.1947. PMID 17770105. Bibcode: 1995Sci...267.1947G. 
  22. ↑ Tarjus, G. (2007). "Materials science: Metal turned to glass". Nature 448 (7155): 758–759. doi:10.1038/448758a. PMID 17700684. Bibcode: 2007Natur.448..758T. 
  23. ↑ Manekar, M. A.; Chaudhary, S.; Chattopadhyay, M. K.; Singh, K. J.; Roy, S. B.; Chaddah, P. (2001). "First-order transition from antiferromagnetism to ferromagnetism inCe(Fe0.96Al0.04)2". Physical Review B 64 (10): 104416. doi:10.1103/PhysRevB.64.104416. ISSN 0163-1829. Bibcode: 2001PhRvB..64j4416M. 
  24. ↑ Banerjee, A.; Pramanik, A. K.; Kumar, Kranti; Chaddah, P. (2006). "Coexisting tunable fractions of glassy and equilibrium long-range-order phases in manganites". Journal of Physics: Condensed Matter 18 (49): L605. doi:10.1088/0953-8984/18/49/L02. Bibcode: 2006JPCM...18L.605B. 
  25. ↑ Wu W.; Israel C.; Hur N.; Park S.; Cheong S. W.; de Lozanne A. (2006). "Magnetic imaging of a supercooling glass transition in a weakly disordered ferromagnet". Nature Materials 5 (11): 881–886. doi:10.1038/nmat1743. PMID 17028576. Bibcode: 2006NatMa...5..881W. 
  26. ↑ Roy, S. B.; Chattopadhyay, M. K.; Chaddah, P.; Moore, J. D.; Perkins, G. K.; Cohen, L. F.; Gschneidner, K. A.; Pecharsky, V. K. (2006). "Evidence of a magnetic glass state in the magnetocaloric material Gd5Ge4". Physical Review B 74 (1): 012403. doi:10.1103/PhysRevB.74.012403. ISSN 1098-0121. Bibcode: 2006PhRvB..74a2403R. 
  27. ↑ Lakhani, Archana; Banerjee, A.; Chaddah, P.; Chen, X.; Ramanujan, R. V. (2012). "Magnetic glass in shape memory alloy: Ni45Co5Mn38Sn12". Journal of Physics: Condensed Matter 24 (38): 386004. doi:10.1088/0953-8984/24/38/386004. ISSN 0953-8984. PMID 22927562. Bibcode: 2012JPCM...24L6004L. 
  28. ↑ Kushwaha, Pallavi; Lakhani, Archana; Rawat, R.; Chaddah, P. (2009). "Low-temperature study of field-induced antiferromagnetic-ferromagnetic transition in Pd-doped Fe-Rh". Physical Review B 80 (17): 174413. doi:10.1103/PhysRevB.80.174413. ISSN 1098-0121. Bibcode: 2009PhRvB..80q4413K. 
  29. ↑ Ivancevic, Vladimir G.; Ivancevic, Tijiana, T. (2008). Complex Nonlinearity. Berlin: Springer. pp. 176–177. ISBN 978-3-540-79357-1. https://books.google.com/books?id=wpsPgHgtxEYC&pg=PA177. Retrieved 12 October 2014. 
  30. ↑ Clark, J.B.; Hastie, J.W.; Kihlborg, L.H.E.; Metselaar, R.; Thackeray, M.M. (1994). "Definitions of terms relating to phase transitions of the solid state". Pure and Applied Chemistry 66 (3): 577–594. doi:10.1351/pac199466030577. 
  31. ↑ Chaisson, Eric J. (2001). Cosmic Evolution. Harvard University Press. ISBN 978-0-674-00342-2. https://archive.org/details/cosmicevolutionr00chai. 
  32. ↑ David Layzer, Cosmogenesis, The Development of Order in the Universe, Oxford Univ. Press, 1991
  33. ↑ Ojovan, Michael I.; Lee, William E. (2006). "Topologically disordered systems at the glass transition". Journal of Physics: Condensed Matter 18 (50): 11507–11520. doi:10.1088/0953-8984/18/50/007. Bibcode: 2006JPCM...1811507O. http://eprints.whiterose.ac.uk/1958/1/ojovanmi1_Topologically2.pdf. 
  34. ↑ Leonard, F.; Delamotte, B. (2015). "Critical exponents can be different on the two sides of a transition". Phys. Rev. Lett. 115 (20): 200601. doi:10.1103/PhysRevLett.115.200601. PMID 26613426. Bibcode: 2015PhRvL.115t0601L. 
  35. ↑ Lipa, J.; Nissen, J.; Stricker, D.; Swanson, D.; Chui, T. (2003). "Specific heat of liquid helium in zero gravity very near the lambda point". Physical Review B 68 (17): 174518. doi:10.1103/PhysRevB.68.174518. Bibcode: 2003PhRvB..68q4518L. 
  36. ↑ Kleinert, Hagen (1999). "Critical exponents from seven-loop strong-coupling φ4 theory in three dimensions". Physical Review D 60 (8): 085001. doi:10.1103/PhysRevD.60.085001. Bibcode: 1999PhRvD..60h5001K. 
  37. ↑ D.Y. Lando and V.B. Teif (2000). "Long-range interactions between ligands bound to a DNA molecule give rise to adsorption with the character of phase transition of the first kind". J. Biomol. Struct. Dyn. 17 (5): 903–911. doi:10.1080/07391102.2000.10506578. PMID 10798534. 
  38. ↑ "13C NMR studies of lipid fatty acyl chains of chloroplast membranes". Indian Journal of Biochemistry and Biophysics 24 (6): 177–178. 1987. doi:10.1016/0165-022X(91)90019-S. PMID 3428918. https://www.researchgate.net/publication/230822408. 
  39. ↑ YashRoy, R C (1990). "Determination of membrane lipid phase transition temperature from 13-C NMR intensities". Journal of Biochemical and Biophysical Methods 20 (4): 353–356. doi:10.1016/0165-022X(90)90097-V. PMID 2365951. https://www.researchgate.net/publication/20790042. 
  40. ↑ Tkacik, Gasper; Mora, Thierry; Marre, Olivier; Amodei, Dario; Berry II, Michael J.; Bialek, William (2014). "Thermodynamics for a network of neurons: Signatures of criticality". arXiv:1407.5946 [q-bio.NC].
  41. ↑ Bialek, W; Cavagna, A; Giardina, I (2014). "Social interactions dominate speed control in poising natural flocks near criticality". PNAS 111 (20): 7212–7217. doi:10.1073/pnas.1324045111. PMID 24785504. Bibcode: 2014PNAS..111.7212B. 
  42. ↑ Krotov, D; Dubuis, J O; Gregor, T; Bialek, W (2014). "Morphogenesis at criticality". PNAS 111 (10): 3683–3688. doi:10.1073/pnas.1324186111. PMID 24516161. Bibcode: 2014PNAS..111.3683K. 
  43. ↑ Mora, Thierry; Bialek, William (2011). "Are biological systems poised at criticality?". Journal of Statistical Physics 144 (2): 268–302. doi:10.1007/s10955-011-0229-4. Bibcode: 2011JSP...144..268M. 
  44. ↑ Schwab, David J; Nemenman, Ilya; Mehta, Pankaj (2014). "Zipf's law and criticality in multivariate data without fine-tuning". Physical Review Letters 113 (6): 068102. doi:10.1103/PhysRevLett.113.068102. PMID 25148352. Bibcode: 2014PhRvL.113f8102S. 
  45. ↑ Longo, G.; Montévil, M. (2011-08-01). "From physics to biology by extending criticality and symmetry breakings". Progress in Biophysics and Molecular Biology. Systems Biology and Cancer 106 (2): 340–347. doi:10.1016/j.pbiomolbio.2011.03.005. PMID 21419157. https://www.academia.edu/23155991. 
  46. ↑ Kelso, J. A. Scott (1995). Dynamic Patterns: The Self-Organization of Brain and Behavior (Complex Adaptive Systems). MIT Press. ISBN 978-0-262-61131-2. 
  47. ↑ Diedrich, F. J.; Warren, W. H. Jr. (1995). "Why change gaits? Dynamics of the walk-run transition". Journal of Experimental Psychology. Human Perception and Performance 21 (1): 183–202. doi:10.1037/0096-1523.21.1.183. PMID 7707029. 
  48. ↑ Hristovski, R.; Balagué, N. (2010). "Fatigue-induced spontaneous termination point--nonequilibrium phase transitions and critical behavior in quasi-isometric exertion". Human Movement Science 29 (4): 483–493. doi:10.1016/j.humov.2010.05.004. PMID 20619908. 
  49. ↑ Moret, Marcelo; Zebende, Gilney (January 2007). "Amino acid hydrophobicity and accessible surface area". Physical Review E 75 (1): 011920. doi:10.1103/PhysRevE.75.011920. PMID 17358197. Bibcode: 2007PhRvE..75a1920M. 
  50. ↑ Gorban, A.N.; Smirnova, E.V.; Tyukina, T.A. (August 2010). "Correlations, risk and crisis: From physiology to finance". Physica A: Statistical Mechanics and Its Applications 389 (16): 3193–3217. doi:10.1016/j.physa.2010.03.035. Bibcode: 2010PhyA..389.3193G. https://www.researchgate.net/publication/222687003. 

Further reading

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Phase_transition&oldid=3280960"
Licensed under CC BY-SA 3.0 | Source: https://handwiki.org/wiki/Physics:Phase_transition
5 views | Status: cached on August 24 2024 17:38:29
↧ Download this article as ZWI file
Encyclosphere.org EncycloReader is supported by the EncyclosphereKSF