Pyramidal carbocation
Topic: Physics
 From HandWiki - Reading time: 10 min
From HandWiki - Reading time: 10 min
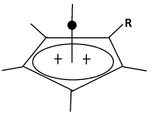
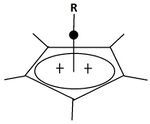
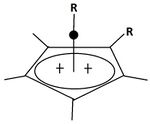
A pyramidal carbocation is a type of carbocation with a specific configuration. This ion exists as a third class, besides the classical and non-classical ions. In these ions, a single carbon atom hovers over a four- or five-sided polygon, in effect forming a pyramid. The four-sided pyramidal ion will carry a charge of 1+, and the five-sided pyramid will carry 2+. In the images (at upper right), the black spot on the vertical line represents the hovering carbon atom.
The apparent coordination number of five, or even six, associated with the carbon atom at the top of the pyramid is a rarity as compared to the usual maximum of four.
History
Studying these cations was sparked, at the time, by amazing results in computational chemistry. While calculating the optimal geometry of the mono-cation which arises from the extraction of chloride from 3-chlorotricyclo[2.1.0.02,5]pentane, the three bridges were expected to orient in space with angles of roughly 120°. The calculations however showed the four-sided pyramid to be the most stable configuration. At the top of this pyramid, there resides a carbon atom, still connected to a hydrogen. The original expected structure turned out to be not even close to an energy minimum: it represented a maximum.[1]
- Figure 1: Several possibilities for (CH)5 cation.
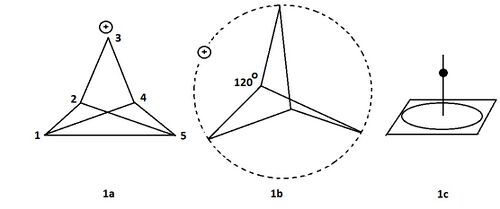
- 1a starting situation in the calculations: the chloride ion just left.
- 1b the expected structure. Charge has been delocalized over three carbon atoms
- 1c representation of the pyramidal ion.
Depending on the method used, the ion 1c in figure 1 is an absolute or just a relative minimum.
Theoretical background
A complete theoretical discussion will use all orbitals of all contributing atoms. A first approximation might use a LCAO of the molecular orbitals in the polygon forming the base of the pyramid and the orbitals on the apical atom, as the carbon atom at the top of the pyramid. This approximation will provide insight into the intrinsic stability of the structures.
Apical carbon atom
The apical carbon atom is connected to only one other substituent, so an sp-hybridisation is to be expected. The substituent will be oriented upward. Towards the basic polygon, three orbitals are available:
- The second sp-orbital. This orbital is relatively low in energy due to the contribution of the s-orbital. With respect to the nodal planes in the remaining p-orbitals the symmetry of this orbital can be written as SxSy,[2] symmetric with respect to both planes. The orbital has a rather low energy, in terms of the Hückel method its value is not easy to estimate, although it will be lower than α, since the orbital will have considerable s-character.
- Two p-orbitals. These orbitals have a higher energy content then the sp-orbital. In terms of the Huckel method, the energy will be α. In symmetry terms, these orbitals are orthogonal, described as AxSy and SxAy[2]
Base of the pyramid
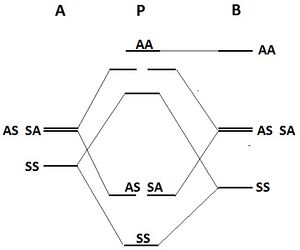
| Figure 2: Orbitals of the apical carbon atom (above) and the MOs of the base (below)[2] |
| 300px |
| Figure 3: Interaction between the apical and basal orbitals. The "A" on top is apical carbon, "P" indicates the pyramidal structure, "B" is for the basal part of the pyramid. |
The approximation for the base of the pyramid is a closed ring of carbon atoms, all of them sp2 hybridised. The exact results depend on the ring size; overall conclusions can be formulated as:
- The lowest molecular orbital has, watched from the apex of the pyramid, no nodal planes. Symmetry will be SxSy.[2] In the Hückel method, its energy is (α - 2β)
- The next level of energy is occupied by two degenerated orbitals. In symmetry terms, they are written as SxAy and AxSy.[2] The energy depends on the size of the ring:
| ring size | energy level |
|---|---|
| 3 | (α + β) |
| 4 | α |
| 5 | (α - 0.618β) |
| 6 | (α - β) |
- Depending on the size of the base, there will be other MOs, but they are irrelevant to the present discussion.
Interaction between apex and base
To obtain bonding interactions between atoms or parts of molecules, two conditions should be met:
- The orbitals to combine should have the same symmetry.
- A smaller difference in energy between the combining orbitals will produce a greater stabilizing effect.
The orbitals at the apical carbon and the basic polygon are able to combine with respect to their symmetries. The result will be a more stable configuration for the pyramids. In figure 2, the symmetry aspects are depicted.
- The apical sp orbital combines with the lowest MO of the basic ring to a low bonding and a high anti-bonding orbital.
- The two apical p orbitals combine with the second lowest energy levels in the basic ring. Two bonding and two anti-bonding orbitals result. Figure 3 is a graphical representation of the results.
Filling the atomic and molecular orbitals in pyramidal structures of different base size leads to the next table. Only bonding orbitals are accounted for.
| n=3 (trigonal) |
n=4 (square) |
n=5 (pentagonal) |
n=6 (hexagonal) | |||||
|---|---|---|---|---|---|---|---|---|
| orbitals | charge | orbitals | charge | orbitals | charge | orbitals | charge | |
| 1s orbitals on carbon | 4 | −8 | 5 | −10 | 6 | −12 | 7 | −14 |
| σ bond between hydrogen and the apical carbon | 1 | −2 | 1 | −2 | 1 | −2 | 1 | −2 |
| σ bond between hydrogen and the basic carbon | 3 | –6 | 4 | –8 | 5 | 10 | 6 | –12 |
| σ bond in between basic carbons | 3 | –6 | 4 | –8 | 5 | –10 | 6 | –12 |
| bonding MO between apical and lowest basic orbital | 1 | –2 | 1 | –2 | 1 | –2 | 1 | –2 |
| bonding MO between apical and second-lowest basic orbitals | 2 | –4 | 2 | –4 | 2 | –4 | 2 | –4 |
| total number of electrons | –28 | –34 | –40 | –46 | ||||
| total nuclear charge: (n+1)*(C+H)=(n+1)*(6+1) | +28 | +35 | +42 | +49 | ||||
| Net charge of structure | 0 | 1+ | 2+ | 3+ | ||||
In the case of the three-sided pyramid, clearly no ion results; a known neutral species arises: tetrahedrane. To this molecule this way of description is an alternative quantum mechanical description.
The other pyramidal structures will be charged in relation with their base size.
Examples
Monocation
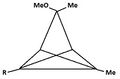
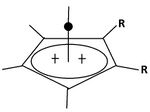
- Figure 4: A number of derivatives of triclo[3,1,0,02,4]pentane (TCP) leading to the same pyramidal cation. The carbon atom carrying the leaving group becomes basic, while carbon at the anti position becomes apical.
The group "R" is either 1H or 2H (D):
In 1972 Masamune describes the results of dissolving a number of precursors to 4d (figure 4) at - 70°C. in superacid (a mixture of SO2ClF and FSO3H). Based on both the 13C as well as the 1H-NMR-spectrum the evidence is clear: in each case the same intermediary is formed. Also, when the super acidic medium is destroyed, with either methanol or benzoic acid, the same product is formed. (see: Reaction... below).[3]
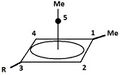
| group/atom( ! ) | 13C | 1H | |
|---|---|---|---|
| 1 | 93.56 | - | 200px |
| 2 / 4 | 73.00 | 4.62 | |
| 3 (if R= 1H) | 60.97 | 4.68 | |
| 5 | -23.04 | - | |
| Methyl at 1 | 7.45 | 2.15 | |
| Methyl at 5 | -1.03 | 1.84 | |
| ( ! )In this table carbon atoms are called, in 1H-NMR the signal of the hydrogen carried by the called carbons are depicted | |||
- Assignment in the hydrogen spectrum is partly on intensity (hydrogens at the basic ring) partly on the common experience hydrogen's at the outer side of a circular conjugated system have signals at higher ppm relative to TMS, while those positioned over the ring will have lower, even negative, signals relative to TMS.
- Assignment in 13C-NMR follow the same considerations as for 1H. Though in carbon NMR intensity is a bad guide to the number of atoms, in the basic ring the unsubstituted carbons are similar enough to use intensity as indication for their number. A powerful tool too is the multiplicity of the carbon signal due to coupling with the to carbon bonded hydrogens.
- Masamune himself does not state anything about the nature of the intermediate ion.[5] Nevertheless, based on rules formulated by Olah,[6] he is able to rule out localized cations (like 1-butyl) or delocalized ones (like allyl). For those ions signals around 200 ppm are expected.
Reaction with methanol and benzoic acid
- Figure 5: De reaction products of the dimethyl pyramidal cation with methanol and benzoic acid.
The "R"-group is either1H or 2H (D):
As described above, independent from its synthetic route, pyramidal ion 5a reacts with methanol or benzoate giving rise to products governed by reagent and the reaction medium as is clear by the substitution patterns. In 1972 Masamune [3][4] is unable to explain the different behavior of the intermediate. In terms of the HSAB-theory an explanation might be given.
In 1975 Masamune calculated[7] in the non-substituted ion most of the charge at the hydrogen atoms. Replacing hydrogen for carbon, the central atom of the methyl group, a more electronegative substituent (2.5 versus 2.1 on the Pauling scale) will concentrate charge on the skeletal carbon. This charge concentration has several effects:
- The reaction with benzoate is governed by π - π interactions. The degeneration in the basic MO-system will be lost because of the presence of a substituting methyl group. As the apical side is inaccessible, benzoate will approach from the bottom side of the pyramid. The interaction between the two π-systems, both disturbed at one point, will force a specific orientation. The orientation in which the interaction between positive charge generated by the methyl group on the pyramid and the charge adjacent to the carboxyl group will direct the system to a reaction of the carboxyl group with carbon 2 or 4 of the pyramid base. When reaction with benzoate takes place at carbon 2 bridges will form between the apical carbon and atoms 1 and 3. A bond too will form between anti-carbon 4 and the apex. Reaction at carbon 4 will have a same effect, although the resulting molecule has a mirror relation with respect to the molecule that results from reaction at position 2.
- The reaction with methanol is charge driven. In de basic system an identifiable center of positive charge is present at the carbon carrying the methyl group. Methanol with its hard base in oxygen, will react at the center of positivity. The methoxy group appears at carbon 1, forcing bridges to form between carbon 2 and 4 to the apex, as well as between the now anti-carbon 3.
Bishomomonocarbocation
In chemistry, the prefix "homo-" denotes a homolog, a likewise compound containing one, or as in this case two, extra CH2-groups. The common aspect of the bishomo ions is the possession of a 1,4-cyclohexadiene ring instead of a cyclobutadiene one.
The stability of this ion at first may seem strange, as enlargement of the ring in general will diminish the bonding overlap between the orbitals at the center of the pyramidal structure. Here the sp2 hybridization, and consequently the planarity of the atoms of and those directly bonded to the sp2 centers, forces the tops of the p-orbitals of the basal carbons towards each other, thus creating a solid base for the apical carbon to sit on. Stiffening the configuration by a bridge between the homo-atoms, converting the base of the pyramid, to a norbornadiene, creates an even more stable structure.
Dication
According to the results presented in Table 1, a five-sided pyramidal carbocation will be divalent. This is confirmed by theoretical[8] and practical work by Hogeveen.[9][10] In contrast to the monocation, which is described with several patterns of substitution, the dication is mainly studied by its hexamethyl derivative. The synthesis starts at hexamethyl Dewar benzene (compound I in table 4) reacting with Cl2 into 5,6-dichloro-1,2,3,4,5,6-hexamethylbicyclo[2.1.1]hex-2-ene (compound II in table 4). Dissolution of this compound in fluorosulfonic acid gives rise to the dication (structure III in table 4).
| 200px | 200px | 200px |
| I: Me6-Dewar benzene | II: Product of reaction of Me6 Dewar benzene with chlorine | III: the pyramidal dication |
The presence of a pyramidal ion in the solution of fluorosulfonic acid is evidenced by the 1H- and 13C-NMR-spectrum (Table 5).
| Intensity | 1H | 13CSingulet | 13CQuartet |
|---|---|---|---|
| 1 | 1.96(s) | 22,5 | - 2.0 |
| 5 | 2,65(s) | 126,3 | 10,6 |
The assignment of the signals is based on their intensities and multiplicities. The assignment of the pyramidal structure is based on the observed simplicity of the spectra: five equal C-CH3 groups combined with one outstanding C-CH3 group. The only way to construct a molecular entity from this data is a five-sided pyramid. Rapid equilibriums between degenerated classical or non-classical carbocations are discarded as the position of the signals does not match the expected values for those kind of structures.[8]
The crystal structure of [C6(CH3)6]2+ (SbF6−)2 • HSO3F was obtained in 2017. Although the apical carbon atom is hexacoordinated, the rule of the tetravalency of carbon is still fulfilled. While the C-CH3 bond length of 1.479(3) Å is typical for a C-C single bond, the other five very long C-C distances of 1.694(2)-1.715(3) Å indicate a bond order of <1.[11]
Reactions of the dication
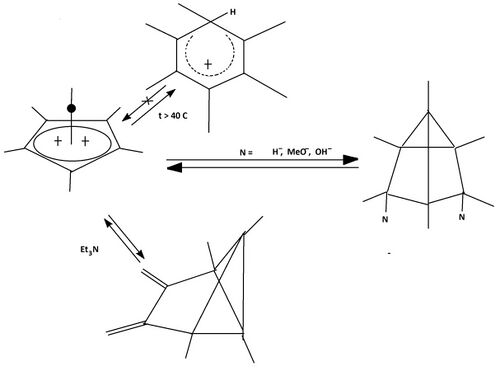
| Figure 6: Reactions of the pyramidal carbodikation |
|---|
|
The reactions of the dication fall apart into three groups:[9][10]
- Thermal reactions The hexamethyl substituted dication is a stable structure up to 40 °C (104 °F). Above this temperature reaction occurs: a hydride-ion is taken up, followed by an irreversible rearrangement to an arenium ion which is stable in the fluorosulfonic acid medium (see: Figure 6, upper reaction).
- Charged nucleophiles (hydride, methoxide, hydroxide) react reversible, leading to, independent of the nucleofile at hand, identical 2,4-substituted tricyclo[3.1.0.03,6]hexane derivatis, e.g.: with methoxide: 2,4-dimethoxy-tricyclo[3.1.0.03,6]hexane is formed (see: Figure 6, middle reaction path).
- Uncharged nucleofiles (amines like triethylamine) act as a base, reversible extracting two hydrogens from the ion, in effect producing a dimethylene derivative of benzvalene (see: Figure 6, lower reaction).
Other substitution patterns at the dications
The product of the reaction of the dication with triethylamine offers a pathway to other substitution patterns then hexamethyl.[12] One or both double bonds are oxidized to a keton. The keton then is reacted with an organometallic compound producing an alkylated hydroxide. The compounds formed in this way possess one or two other alkyl groups, depending on the number of oxidized double bonds. When the alcohols are dissolved in fluorosulfonic acid, they again give rise to new pyramidal dications. Both non-methyl groups occupy basal positions. Each other position at the pyramidal skeleton still carries a methyl group. Table 6 summarizes these findings.
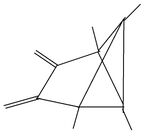
|
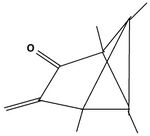
|
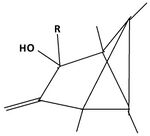
|
|
|
| I: Reactionproduct with Et3N | II: The monoketon | III: alkylated monoalcohol | IV: The pyramidal ion when dissolved the first time in FSO3H | V: The pyramidal cation when dissolved a second time in FSO3H |
|

|
|
| |
| II: The diketon | III: alkylated diol | IV: The pyramidal ion when dissolved the first time in FSO3H | V: The pyramidal cation when dissolved a second time in FSO3H |
Up to this point the substitution pattern of the divalent pyramidal ion is of minor importance to its behavior. A clear difference arises when the thermal stability if the ions of type V (Table 6) is studied: at −40 °C (−40 °F) the apical ethyl substituted ion is stable for 48 hours, whereas no trace of the apical iso-propyl ion is detectable anymore.
Tervalent and higher ions
At the time of the literature survey (end of 1978), there were no reports on tervalent or higher pyramidal cations.
Notes and References
- ↑ Stohrer, W.D.; Hoffmann, R. (1972). "Bond-stretch isomerism and polytopal rearrangements in (CH)5+, (CH)5-, and (CH)4CO". J. Am. Chem. Soc. 94 (5): 1661–1668. doi:10.1021/ja00760a039.
- ↑ 2.0 2.1 2.2 2.3 2.4 S indicating the orbital is symmetric with respect to the plane indicated by the subscript. An A describes an anti-symmetry with respect to the by the subscript indicated plane.
- ↑ 3.0 3.1 Masamune, S.; Sakai, M.; Ona, H. (1972). "Nature of the (CH)5+ species. I. Solvolysis of 1,5-dimethyltricyclo[2.1.0.02,5]pent-3-yl benzoate". J. Am. Chem. Soc. 94 (25): 8955–8956. doi:10.1021/ja00780a078.
- ↑ 4.0 4.1 S. Masamune, S.; Sakai, M.; Ona, H.; Jones, A.J. (1972). "Nature of the (CH)5+ species. II. Direct observation of the carbonium ion of 3-hydroxyhomotetrahedrane derivatives". J. Am. Chem. Soc. 94 (25): 8956. doi:10.1021/ja00780a079.
- ↑ Although Masamune presents his practical results later the same year as Stöhrer and Hoffmann their theoretical ones, it is unlikely Masamune was able to edit his paper at the moment the implications of the theoretical work became clear.
- ↑ Olah, G.A.; Donovan, D.J.; Prakash, G. (1978). "The α, 1-dimethylcyclopropylcarbinyl cation". Tetrahedron Letters 19 (48): 4779–4782. doi:10.1016/s0040-4039(01)85729-4.
- ↑ Masamune, S. (1975). "Some aspects of strained systems. [4]Annulene and its CH+ adduct". Pure and Applied Chemistry 44 (4): 861–884. doi:10.1351/pac197544040861.
- ↑ 8.0 8.1 Hogeveen, H.; Kwant, P. W.; Postma, J.; van Duynen, P. Th. (1974). "Electronic spectra of pyramidal dications, (CCH3)62+ and (CCH)62+". Tetrahedron Letters 15 (49–50): 4351–4354. doi:10.1016/S0040-4039(01)92161-6.
- ↑ 9.0 9.1 Hogeveen, H.; Kwant, P. W. (1974). "Chemistry and spectroscopy in strongly acidic solutions. XL. (CCH3)62+, an unusual dication". Journal of the American Chemical Society 96 (7): 2208–2214. doi:10.1021/ja00814a034.
- ↑ 10.0 10.1 Hogeveen, H.; Kwant, P. W. (1973). "Direct observation of a remarkably stable dication of unusual structure: (CCH3)62⊕". Tetrahedron Letters 14 (19): 1665–1670. doi:10.1016/S0040-4039(01)96023-X.
- ↑ Malischewski, Moritz; Seppelt, K. (2016-11-25). "Crystal Structure Determination of the Pentagonal-Pyramidal Hexamethylbenzene Dication C6(CH3)6 2+" (in en). Angewandte Chemie International Edition 56 (1): 368–370. doi:10.1002/anie.201608795. ISSN 1433-7851. PMID 27885766.
- ↑ G. Giordano, G.; Heldeweg, R.; Hogeveen, H. (1977). "Pyramidal dications. Introduction of basal and apical substituents". J. Am. Chem. Soc. 99 (15): 5181–5183. doi:10.1021/ja00457a050.
 |
 KSF
KSF