Quantum chromodynamics

Standard Model of particle physics
Elementary particles of the Standard Model
Background Particle physics Standard Model Quantum field theory Gauge theory Spontaneous symmetry breaking Higgs mechanism
Constituents Electroweak interaction Quantum chromodynamics CKM matrix Standard Model mathematics
Limitations Strong CP problem Hierarchy problem Neutrino oscillations Physics beyond the Standard Model
v t e

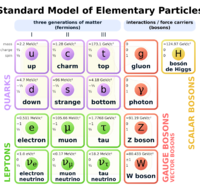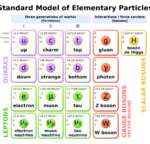
In theoretical physics, quantum chromodynamics (QCD) is the theory of the strong interaction between quarks mediated by gluons. Quarks are fundamental particles that make up composite hadrons such as the proton, neutron and pion. QCD is a type of quantum field theory called a non-abelian gauge theory, with symmetry group SU(3). The QCD analog of electric charge is a property called color. Gluons are the force carriers of the theory, just as photons are for the electromagnetic force in quantum electrodynamics. The theory is an important part of the Standard Model of particle physics. A large body of experimental evidence for QCD has been gathered over the years.

QCD exhibits three salient properties:

• Color confinement. Due to the force between two color charges remaining constant as they are separated, the energy grows until a quark–antiquark pair is spontaneously produced, turning the initial hadron into a pair of hadrons instead of isolating a color charge. Although analytically unproven, color confinement is well established from lattice QCD calculations and decades of experiments.^[1]
• Asymptotic freedom, a steady reduction in the strength of interactions between quarks and gluons as the energy scale of those interactions increases (and the corresponding length scale decreases). The asymptotic freedom of QCD was discovered in 1973 by David Gross and Frank Wilczek,^[2] and independently by David Politzer in the same year.^[3] For this work, all three shared the 2004 Nobel Prize in Physics.^[4]
• Chiral symmetry breaking, the spontaneous symmetry breaking of an important global symmetry of quarks, detailed below, with the result of generating masses for hadrons far above the masses of the quarks, and making pseudoscalar mesons exceptionally light. Yoichiro Nambu was awarded the 2008 Nobel Prize in Physics for elucidating the phenomenon, a dozen years before the advent of QCD. Lattice simulations have confirmed all his generic predictions.

Terminology

Physicist Murray Gell-Mann coined the word quark in its present sense. It originally comes from the phrase "Three quarks for Muster Mark" in Finnegans Wake by James Joyce. On June 27, 1978, Gell-Mann wrote a private letter to the editor of the Oxford English Dictionary, in which he related that he had been influenced by Joyce's words: "The allusion to three quarks seemed perfect." (Originally, only three quarks had been discovered.)^[5]

The three kinds of charge in QCD (as opposed to one in quantum electrodynamics or QED) are usually referred to as "color charge" by loose analogy to the three kinds of color (red, green and blue) perceived by humans. Other than this nomenclature, the quantum parameter "color" is completely unrelated to the everyday, familiar phenomenon of color.

The force between quarks is known as the colour force^[6] (or color force^[7]) or strong interaction, and is responsible for the nuclear force.

Since the theory of electric charge is dubbed "electrodynamics", the Greek word χρῶμα (chrōma, "color") is applied to the theory of color charge, "chromodynamics".

History

Main pages: Physics:History of quantum mechanics and Physics:History of quantum field theory

With the invention of bubble chambers and spark chambers in the 1950s, experimental particle physics discovered a large and ever-growing number of particles called hadrons. It seemed that such a large number of particles could not all be fundamental. First, the particles were classified by charge and isospin by Eugene Wigner and Werner Heisenberg; then, in 1953–56,^[8][9][10] according to strangeness by Murray Gell-Mann and Kazuhiko Nishijima (see Gell-Mann–Nishijima formula). To gain greater insight, the hadrons were sorted into groups having similar properties and masses using the eightfold way, invented in 1961 by Gell-Mann^[11] and Yuval Ne'eman. Gell-Mann and George Zweig, correcting an earlier approach of Shoichi Sakata, went on to propose in 1963 that the structure of the groups could be explained by the existence of three flavors of smaller particles inside the hadrons: the quarks. Gell-Mann also briefly discussed a field theory model in which quarks interact with gluons.^[12][13]

Perhaps the first remark that quarks should possess an additional quantum number was made^[14] as a short footnote in the preprint of Boris Struminsky^[15] in connection with the Ω⁻ hyperon being composed of three strange quarks with parallel spins (this situation was peculiar, because since quarks are fermions, such a combination is forbidden by the Pauli exclusion principle):

Three identical quarks cannot form an antisymmetric S-state. In order to realize an antisymmetric orbital S-state, it is necessary for the quark to have an additional quantum number.

Boris Struminsky was a PhD student of Nikolay Bogolyubov. The problem considered in this preprint was suggested by Nikolay Bogolyubov, who advised Boris Struminsky in this research.^[15] In the beginning of 1965, Nikolay Bogolyubov, Boris Struminsky and Albert Tavkhelidze wrote a preprint with a more detailed discussion of the additional quark quantum degree of freedom.^[16] This work was also presented by Albert Tavkhelidze without obtaining consent of his collaborators for doing so at an international conference in Trieste (Italy), in May 1965.^[17][18]

A similar mysterious situation was with the Δ⁺⁺ baryon; in the quark model, it is composed of three up quarks with parallel spins. In 1964–65, Greenberg^[19] and Han–Nambu^[20] independently resolved the problem by proposing that quarks possess an additional SU(3) gauge degree of freedom, later called color charge. Han and Nambu noted that quarks might interact via an octet of vector gauge bosons: the gluons.

Since free quark searches consistently failed to turn up any evidence for the new particles, and because an elementary particle back then was defined as a particle that could be separated and isolated, Gell-Mann often said that quarks were merely convenient mathematical constructs, not real particles. The meaning of this statement was usually clear in context: He meant quarks are confined, but he also was implying that the strong interactions could probably not be fully described by quantum field theory.

Richard Feynman argued that high energy experiments showed quarks are real particles: he called them partons (since they were parts of hadrons). By particles, Feynman meant objects that travel along paths, elementary particles in a field theory.

The difference between Feynman's and Gell-Mann's approaches reflected a deep split in the theoretical physics community. Feynman thought the quarks have a distribution of position or momentum, like any other particle, and he (correctly) believed that the diffusion of parton momentum explained diffractive scattering. Although Gell-Mann believed that certain quark charges could be localized, he was open to the possibility that the quarks themselves could not be localized because space and time break down. This was the more radical approach of S-matrix theory.

James Bjorken proposed that pointlike partons would imply certain relations in deep inelastic scattering of electrons and protons, which were verified in experiments at SLAC in 1969. This led physicists to abandon the S-matrix approach for the strong interactions.

In 1973 the concept of color as the source of a "strong field" was developed into the theory of QCD by physicists Harald Fritzsch and Heinrich Leutwyler, together with physicist Murray Gell-Mann.^[21] In particular, they employed the general field theory developed in 1954 by Chen Ning Yang and Robert Mills^[22] (see Yang–Mills theory), in which the carrier particles of a force can themselves radiate further carrier particles. (This is different from QED, where the photons that carry the electromagnetic force do not radiate further photons.)

The discovery of asymptotic freedom in the strong interactions by David Gross, David Politzer and Frank Wilczek allowed physicists to make precise predictions of the results of many high energy experiments using the quantum field theory technique of perturbation theory. Evidence of gluons was discovered in three-jet events at PETRA in 1979. These experiments became more and more precise, culminating in the verification of perturbative QCD at the level of a few percent at LEP, at CERN.

The other side of asymptotic freedom is confinement. Since the force between color charges does not decrease with distance, it is believed that quarks and gluons can never be liberated from hadrons. This aspect of the theory is verified within lattice QCD computations, but is not mathematically proven. One of the Millennium Prize Problems announced by the Clay Mathematics Institute requires a claimant to produce such a proof. Other aspects of non-perturbative QCD are the exploration of phases of quark matter, including the quark–gluon plasma.

The relation between the short-distance particle limit and the confining long-distance limit is one of the topics recently explored using string theory, the modern form of S-matrix theory.^[23][24]

Theory

Some definitions

Unsolved problem in physics: QCD in the non-perturbative regime: Confinement: the equations of QCD remain unsolved at energy scales relevant for describing atomic nuclei. How does QCD give rise to the physics of nuclei and nuclear constituents? Quark matter: the equations of QCD predict that a plasma (or soup) of quarks and gluons should be formed at high temperature and density. What are the properties of this phase of matter? (more unsolved problems in physics)

Every field theory of particle physics is based on certain symmetries of nature whose existence is deduced from observations. These can be

• local symmetries, which are the symmetries that act independently at each point in spacetime. Each such symmetry is the basis of a gauge theory and requires the introduction of its own gauge bosons.
• global symmetries, which are symmetries whose operations must be simultaneously applied to all points of spacetime.

QCD is a non-abelian gauge theory (or Yang–Mills theory) of the SU(3) gauge group obtained by taking the color charge to define a local symmetry.

Since the strong interaction does not discriminate between different flavors of quark, QCD has approximate flavor symmetry, which is broken by the differing masses of the quarks.

There are additional global symmetries whose definitions require the notion of chirality, discrimination between left and right-handed. If the spin of a particle has a positive projection on its direction of motion then it is called right-handed; otherwise, it is left-handed. Chirality and handedness are not the same, but become approximately equivalent at high energies.

• Chiral symmetries involve independent transformations of these two types of particle.
• Vector symmetries (also called diagonal symmetries) mean the same transformation is applied on the two chiralities.
• Axial symmetries are those in which one transformation is applied on left-handed particles and the inverse on the right-handed particles.

Additional remarks: duality

As mentioned, asymptotic freedom means that at large energy – this corresponds also to short distances – there is practically no interaction between the particles. This is in contrast – more precisely one would say dual– to what one is used to, since usually one connects the absence of interactions with large distances. However, as already mentioned in the original paper of Franz Wegner,^[25] a solid state theorist who introduced 1971 simple gauge invariant lattice models, the high-temperature behaviour of the original model, e.g. the strong decay of correlations at large distances, corresponds to the low-temperature behaviour of the (usually ordered!) dual model, namely the asymptotic decay of non-trivial correlations, e.g. short-range deviations from almost perfect arrangements, for short distances. Here, in contrast to Wegner, we have only the dual model, which is that one described in this article.^[26]

Symmetry groups

The color group SU(3) corresponds to the local symmetry whose gauging gives rise to QCD. The electric charge labels a representation of the local symmetry group U(1), which is gauged to give QED: this is an abelian group. If one considers a version of QCD with N_f flavors of massless quarks, then there is a global (chiral) flavor symmetry group SU_L(N_f) × SU_R(N_f) × U_B(1) × U_A(1). The chiral symmetry is spontaneously broken by the QCD vacuum to the vector (L+R) SU_V(N_f) with the formation of a chiral condensate. The vector symmetry, U_B(1) corresponds to the baryon number of quarks and is an exact symmetry. The axial symmetry U_A(1) is exact in the classical theory, but broken in the quantum theory, an occurrence called an anomaly. Gluon field configurations called instantons are closely related to this anomaly.

There are two different types of SU(3) symmetry: there is the symmetry that acts on the different colors of quarks, and this is an exact gauge symmetry mediated by the gluons, and there is also a flavor symmetry that rotates different flavors of quarks to each other, or flavor SU(3). Flavor SU(3) is an approximate symmetry of the vacuum of QCD, and is not a fundamental symmetry at all. It is an accidental consequence of the small mass of the three lightest quarks.

In the QCD vacuum there are vacuum condensates of all the quarks whose mass is less than the QCD scale. This includes the up and down quarks, and to a lesser extent the strange quark, but not any of the others. The vacuum is symmetric under SU(2) isospin rotations of up and down, and to a lesser extent under rotations of up, down, and strange, or full flavor group SU(3), and the observed particles make isospin and SU(3) multiplets.

The approximate flavor symmetries do have associated gauge bosons, observed particles like the rho and the omega, but these particles are nothing like the gluons and they are not massless. They are emergent gauge bosons in an approximate string description of QCD.

Lagrangian

The dynamics of the quarks and gluons are defined by the quantum chromodynamics Lagrangian. The gauge invariant QCD Lagrangian is

where [math]\displaystyle{ \psi_i(x) \, }[/math] is the quark field, a dynamical function of spacetime, in the fundamental representation of the SU(3) gauge group, indexed by [math]\displaystyle{ i }[/math] and [math]\displaystyle{ j }[/math] running from [math]\displaystyle{ 1 }[/math] to [math]\displaystyle{ 3 }[/math]; [math]\displaystyle{ D_\mu }[/math] is the gauge covariant derivative; the γ^μ are Gamma matrices connecting the spinor representation to the vector representation of the Lorentz group.

Herein, the gauge covariant derivative [math]\displaystyle{ \left( D_\mu \right)_{ij} = \partial_\mu \delta_{ij} - i g \left( T_a \right)_{ij} \mathcal{A}^a_\mu \, }[/math]couples the quark field with a coupling strength [math]\displaystyle{ g \, }[/math]to the gluon fields via the infinitesimal SU(3) generators [math]\displaystyle{ T_a \, }[/math]in the fundamental representation. An explicit representation of these generators is given by [math]\displaystyle{ T_a = \lambda_a / 2 \, }[/math], wherein the [math]\displaystyle{ \lambda_a \, (a = 1 \ldots 8)\, }[/math]are the Gell-Mann matrices.

The symbol [math]\displaystyle{ G^a_{\mu \nu} \, }[/math] represents the gauge invariant gluon field strength tensor, analogous to the electromagnetic field strength tensor, F^μν, in quantum electrodynamics. It is given by:^[27]

[math]\displaystyle{ G^a_{\mu \nu} = \partial_\mu \mathcal{A}^a_\nu - \partial_\nu \mathcal{A}^a_\mu + g f^{abc} \mathcal{A}^b_\mu \mathcal{A}^c_\nu \,, }[/math]

where [math]\displaystyle{ \mathcal{A}^a_\mu(x) \, }[/math] are the gluon fields, dynamical functions of spacetime, in the adjoint representation of the SU(3) gauge group, indexed by a, b and c running from [math]\displaystyle{ 1 }[/math] to [math]\displaystyle{ 8 }[/math]; and f_abc are the structure constants of SU(3) (the generators of the adjoint representation). Note that the rules to move-up or pull-down the a, b, or c indices are trivial, (+, ..., +), so that f^abc = f_abc = f^a_bc whereas for the μ or ν indices one has the non-trivial relativistic rules corresponding to the metric signature (+ − − −).

The variables m and g correspond to the quark mass and coupling of the theory, respectively, which are subject to renormalization.

An important theoretical concept is the Wilson loop (named after Kenneth G. Wilson). In lattice QCD, the final term of the above Lagrangian is discretized via Wilson loops, and more generally the behavior of Wilson loops can distinguish confined and deconfined phases.

Fields

The pattern of strong charges for the three colors of quark, three antiquarks, and eight gluons (with two of zero charge overlapping).

Quarks are massive spin-​¹⁄₂ fermions that carry a color charge whose gauging is the content of QCD. Quarks are represented by Dirac fields in the fundamental representation 3 of the gauge group SU(3). They also carry electric charge (either −​¹⁄₃ or +​²⁄₃) and participate in weak interactions as part of weak isospin doublets. They carry global quantum numbers including the baryon number, which is ​¹⁄₃ for each quark, hypercharge and one of the flavor quantum numbers.

Gluons are spin-1 bosons that also carry color charges, since they lie in the adjoint representation 8 of SU(3). They have no electric charge, do not participate in the weak interactions, and have no flavor. They lie in the singlet representation 1 of all these symmetry groups.

Each type of quark has a corresponding antiquark, of which the charge is exactly opposite. They transform in the conjugate representation to quarks, denoted [math]\displaystyle{ \bar\mathbf{3} }[/math].

Dynamics

According to the rules of quantum field theory, and the associated Feynman diagrams, the above theory gives rise to three basic interactions: a quark may emit (or absorb) a gluon, a gluon may emit (or absorb) a gluon, and two gluons may directly interact. This contrasts with QED, in which only the first kind of interaction occurs, since photons have no charge. Diagrams involving Faddeev–Popov ghosts must be considered too (except in the unitarity gauge).

Area law and confinement

Detailed computations with the above-mentioned Lagrangian^[28] show that the effective potential between a quark and its anti-quark in a meson contains a term that increases in proportion to the distance between the quark and anti-quark ([math]\displaystyle{ \propto r }[/math]), which represents some kind of "stiffness" of the interaction between the particle and its anti-particle at large distances, similar to the entropic elasticity of a rubber band (see below). This leads to confinement ^[29] of the quarks to the interior of hadrons, i.e. mesons and nucleons, with typical radii R_c, corresponding to former "Bag models" of the hadrons^[30] The order of magnitude of the "bag radius" is 1 fm (= 10⁻¹⁵ m). Moreover, the above-mentioned stiffness is quantitatively related to the so-called "area law" behavior of the expectation value of the Wilson loop product P_W of the ordered coupling constants around a closed loop W; i.e. [math]\displaystyle{ \,\langle P_W\rangle }[/math] is proportional to the area enclosed by the loop. For this behavior the non-abelian behavior of the gauge group is essential.

Methods

Further analysis of the content of the theory is complicated. Various techniques have been developed to work with QCD. Some of them are discussed briefly below.

Perturbative QCD

Main page: Physics:Perturbative QCD

This approach is based on asymptotic freedom, which allows perturbation theory to be used accurately in experiments performed at very high energies. Although limited in scope, this approach has resulted in the most precise tests of QCD to date.

Lattice QCD

Main page: Physics:Lattice QCD

⟨E²⟩ plot for static quark–antiquark system held at a fixed separation, where blue is zero and red is the highest value (result of a lattice QCD simulation by M. Cardoso et al.^[31])

Among non-perturbative approaches to QCD, the most well established is lattice QCD. This approach uses a discrete set of spacetime points (called the lattice) to reduce the analytically intractable path integrals of the continuum theory to a very difficult numerical computation that is then carried out on supercomputers like the QCDOC, which was constructed for precisely this purpose. While it is a slow and resource-intensive approach, it has wide applicability, giving insight into parts of the theory inaccessible by other means, in particular into the explicit forces acting between quarks and antiquarks in a meson. However, the numerical sign problem makes it difficult to use lattice methods to study QCD at high density and low temperature (e.g. nuclear matter or the interior of neutron stars).

1/N expansion

A well-known approximation scheme, the ​¹⁄_N expansion, starts from the idea that the number of colors is infinite, and makes a series of corrections to account for the fact that it is not. Until now, it has been the source of qualitative insight rather than a method for quantitative predictions. Modern variants include the AdS/CFT approach.

Effective theories

For specific problems, effective theories may be written down that give qualitatively correct results in certain limits. In the best of cases, these may then be obtained as systematic expansions in some parameters of the QCD Lagrangian. One such effective field theory is chiral perturbation theory or ChiPT, which is the QCD effective theory at low energies. More precisely, it is a low energy expansion based on the spontaneous chiral symmetry breaking of QCD, which is an exact symmetry when quark masses are equal to zero, but for the u, d and s quark, which have small mass, it is still a good approximate symmetry. Depending on the number of quarks that are treated as light, one uses either SU(2) ChiPT or SU(3) ChiPT. Other effective theories are heavy quark effective theory (which expands around heavy quark mass near infinity), and soft-collinear effective theory (which expands around large ratios of energy scales). In addition to effective theories, models like the Nambu–Jona-Lasinio model and the chiral model are often used when discussing general features.

QCD sum rules

Main page: Physics:QCD sum rules

Based on an Operator product expansion one can derive sets of relations that connect different observables with each other.

Experimental tests

The notion of quark flavors was prompted by the necessity of explaining the properties of hadrons during the development of the quark model. The notion of color was necessitated by the puzzle of the Δ⁺⁺. This has been dealt with in the section on the history of QCD.

The first evidence for quarks as real constituent elements of hadrons was obtained in deep inelastic scattering experiments at SLAC. The first evidence for gluons came in three-jet events at PETRA.^[32]

Several good quantitative tests of perturbative QCD exist:

• The running of the QCD coupling as deduced from many observations
• Scaling violation in polarized and unpolarized deep inelastic scattering
• Vector boson production at colliders (this includes the Drell–Yan process)
• Direct photons produced in hadronic collisions
• Jet cross sections in colliders
• Event shape observables at the LEP
• Heavy-quark production in colliders

Quantitative tests of non-perturbative QCD are fewer, because the predictions are harder to make. The best is probably the running of the QCD coupling as probed through lattice computations of heavy-quarkonium spectra. There is a recent claim about the mass of the heavy meson B_c . Other non-perturbative tests are currently at the level of 5% at best. Continuing work on masses and form factors of hadrons and their weak matrix elements are promising candidates for future quantitative tests. The whole subject of quark matter and the quark–gluon plasma is a non-perturbative test bed for QCD that still remains to be properly exploited.^{[citation needed]}

One qualitative prediction of QCD is that there exist composite particles made solely of gluons called glueballs that have not yet been definitively observed experimentally. A definitive observation of a glueball with the properties predicted by QCD would strongly confirm the theory. In principle, if glueballs could be definitively ruled out, this would be a serious experimental blow to QCD. But, as of 2013, scientists are unable to confirm or deny the existence of glueballs definitively, despite the fact that particle accelerators have sufficient energy to generate them.

Cross-relations to condensed matter physics

There are unexpected cross-relations to condensed matter physics. For example, the notion of gauge invariance forms the basis of the well-known Mattis spin glasses,^[33] which are systems with the usual spin degrees of freedom [math]\displaystyle{ s_i=\pm 1\, }[/math] for i =1,...,N, with the special fixed "random" couplings [math]\displaystyle{ J_{i,k}=\epsilon_i \,J_0\,\epsilon_k\,. }[/math] Here the ε_i and ε_k quantities can independently and "randomly" take the values ±1, which corresponds to a most-simple gauge transformation [math]\displaystyle{ (\,s_i\to s_i\cdot\epsilon_i\quad\,J_{i,k}\to \epsilon_i J_{i,k}\epsilon_k\,\quad s_k\to s_k\cdot\epsilon_k \,)\,. }[/math] This means that thermodynamic expectation values of measurable quantities, e.g. of the energy [math]\displaystyle{ {\mathcal H}:=-\sum s_i\,J_{i,k}\,s_k\,, }[/math] are invariant.

However, here the coupling degrees of freedom [math]\displaystyle{ J_{i,k} }[/math], which in the QCD correspond to the gluons, are "frozen" to fixed values (quenching). In contrast, in the QCD they "fluctuate" (annealing), and through the large number of gauge degrees of freedom the entropy plays an important role (see below).

For positive J₀ the thermodynamics of the Mattis spin glass corresponds in fact simply to a "ferromagnet in disguise", just because these systems have no "frustration" at all. This term is a basic measure in spin glass theory.^[34] Quantitatively it is identical with the loop product [math]\displaystyle{ P_W:\,=\,J_{i,k}J_{k,l}...J_{n,m}J_{m,i} }[/math] along a closed loop W. However, for a Mattis spin glass – in contrast to "genuine" spin glasses – the quantity P_W never becomes negative.

The basic notion "frustration" of the spin-glass is actually similar to the Wilson loop quantity of the QCD. The only difference is again that in the QCD one is dealing with SU(3) matrices, and that one is dealing with a "fluctuating" quantity. Energetically, perfect absence of frustration should be non-favorable and atypical for a spin glass, which means that one should add the loop product to the Hamiltonian, by some kind of term representing a "punishment". In the QCD the Wilson loop is essential for the Lagrangian rightaway.

The relation between the QCD and "disordered magnetic systems" (the spin glasses belong to them) were additionally stressed in a paper by Fradkin, Huberman and Shenker,^[35] which also stresses the notion of duality.

A further analogy consists in the already mentioned similarity to polymer physics, where, analogously to Wilson loops, so-called "entangled nets" appear, which are important for the formation of the entropy-elasticity (force proportional to the length) of a rubber band. The non-abelian character of the SU(3) corresponds thereby to the non-trivial "chemical links", which glue different loop segments together, and "asymptotic freedom" means in the polymer analogy simply the fact that in the short-wave limit, i.e. for [math]\displaystyle{ 0\leftarrow\lambda_w\ll R_c }[/math] (where R_c is a characteristic correlation length for the glued loops, corresponding to the above-mentioned "bag radius", while λ_w is the wavelength of an excitation) any non-trivial correlation vanishes totally, as if the system had crystallized.^[36]

There is also a correspondence between confinement in QCD – the fact that the color field is only different from zero in the interior of hadrons – and the behaviour of the usual magnetic field in the theory of type-II superconductors: there the magnetism is confined to the interior of the Abrikosov flux-line lattice,^[37] i.e., the London penetration depth λ of that theory is analogous to the confinement radius R_c of quantum chromodynamics. Mathematically, this correspondendence is supported by the second term, [math]\displaystyle{ \propto g G^a_\mu \bar{\psi}_i \gamma^\mu T^a_{ij} \psi_j\,, }[/math] on the r.h.s. of the Lagrangian.

See also

• For overviews:
  • Standard Model
  • Strong interaction
  • Quark
  • Gluon
  • Hadron
  • Color confinement
  • QCD matter
  • Quark–gluon plasma
• For details:
  • Gauge theory
  • Quantum gauge theory, BRST quantization and Faddeev–Popov ghost
  • Quantum field theory – a more general category
• For techniques:
  • Lattice QCD
  • 1/N expansion
  • Perturbative QCD
  • Soft-collinear effective theory
  • Heavy quark effective theory
  • Chiral model
  • Nambu–Jona-Lasinio model
• For experiments:
  • Deep inelastic scattering
  • Jet (particle physics)
  • Quark–gluon plasma
• Quantum electrodynamics
• Symmetry in quantum mechanics
• Yang–Mills theory
• Yang–Mills existence and mass gap

References

Further reading

• Greiner, Walter; Schramm, Stefan; Stein, Eckart (2007). Quantum Chromodynamics. Berlin Heidelberg: Springer. ISBN 978-3-540-48535-3. https://www.springer.com/gp/book/9783540485346#otherversion=9783540485353. 
• Halzen, Francis; Martin, Alan (1984). Quarks & Leptons: An Introductory Course in Modern Particle Physics. John Wiley & Sons. ISBN 978-0-471-88741-6. https://archive.org/details/quarksleptonsint0000halz. 
• Creutz, Michael (1985). Quarks, Gluons and Lattices. Cambridge University Press. ISBN 978-0-521-31535-7. 

External links

• Frank Wilczek (2000). "QCD made simple". Physics Today 53 (8): 22–28. doi:10.1063/1.1310117. Bibcode: 2000PhT....53h..22W. http://frankwilczek.com/Wilczek_Easy_Pieces/298_QCD_Made_Simple.pdf. 
• Particle data group
• The millennium prize for proving confinement
• Ab Initio Determination of Light Hadron Masses
• Andreas S Kronfeld The Weight of the World Is Quantum Chromodynamics
• Andreas S Kronfeld Quantum chromodynamics with advanced computing
• Standard model gets right answer
• Quantum Chromodynamics
• Cern Courier, The history of QCD with Prof. Dr. Harald Fritzsch

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Quantum chromodynamics. Read more