Table of Contents Categories
Quantum number
Topic: Physics
From HandWiki - Reading time: 13 min
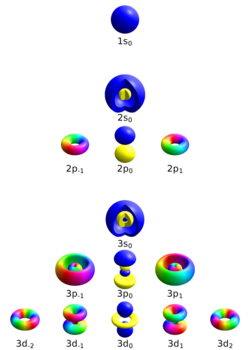
| Part of a series on |
| Quantum mechanics |
|---|
| [math]\displaystyle{ i \hbar \frac{\partial}{\partial t} | \psi (t) \rangle = \hat{H} | \psi (t) \rangle }[/math] |
In quantum physics and chemistry, quantum numbers describe values of conserved quantities in the dynamics of a quantum system. Quantum numbers correspond to eigenvalues of operators that commute with the Hamiltonian—quantities that can be known with precision at the same time as the system's energy[note 1]—and their corresponding eigenspaces. Together, a specification of all of the quantum numbers of a quantum system fully characterize a basis state of the system, and can in principle be measured together.
An important aspect of quantum mechanics is the quantization of many observable quantities of interest.[note 2] In particular, this leads to quantum numbers that take values in discrete sets of integers or half-integers; although they could approach infinity in some cases. This distinguishes quantum mechanics from classical mechanics where the values that characterize the system such as mass, charge, or momentum, all range continuously. Quantum numbers often describe specifically the energy levels of electrons in atoms, but other possibilities include angular momentum, spin, etc. An important family is flavour quantum numbers – internal quantum numbers which determine the type of a particle and its interactions with other particles through the fundamental forces. Any quantum system can have one or more quantum numbers; it is thus difficult to list all possible quantum numbers.
Quantum numbers needed for a given system
The tally of quantum numbers varies from system to system and has no universal answer. Hence these parameters must be found for each system to be analyzed. A quantized system requires at least one quantum number. The dynamics (i.e. time evolution) of any quantum system are described by a quantum operator in the form of a Hamiltonian, H. There is one quantum number of the system corresponding to the system's energy; i.e., one of the eigenvalues of the Hamiltonian. There is also one quantum number for each linearly independent operator O that commutes with the Hamiltonian. A complete set of commuting observables (CSCO) that commute with the Hamiltonian characterizes the system with all its quantum numbers. There is a one-to-one relationship between the quantum numbers and the operators of the CSCO, with each quantum number taking one of the eigenvalues of its corresponding operator. As a result of the different basis that may be arbitrarily chosen to form a complete set of commuting operators, different sets of quantum numbers may be used for the description of the same system in different situations.
Electron in an atom
Four quantum numbers can describe an electron in an atom completely:
- Principal quantum number (n)
- Azimuthal quantum number (ℓ)
- Magnetic quantum number (mℓ)
- Spin quantum number (ms)
The spin–orbital interaction, however, relates these numbers. Thus, a complete description of the system can be given with fewer quantum numbers, if orthogonal choices are made for these basis vectors.
Specificity
Different electrons in a system will have different quantum numbers. For example, the highest occupied orbital electron, the actual differentiating electron (i.e. the electron that differentiates an element from the previous one), or the differentiating electron according to the aufbau approximation. In lanthanum, as a further illustration, the electrons involved are in the 6s; 5d; and 4f orbitals, respectively. In this case the principal quantum numbers are 6, 5, and 4.
Common terminology
The model used here describes electrons using four quantum numbers, n, ℓ, mℓ, ms, given below. It is also the common nomenclature in the classical description of nuclear particle states (e.g. protons and neutrons). A quantum description of molecular orbitals require other quantum numbers, because the Hamiltonian and its symmetries are different.
Principal quantum number
The principal quantum number describes the electron shell, or energy level, of an electron. The value of n ranges from 1 to the shell containing the outermost electron of that atom, that is[1]
- n = 1, 2, ...
For example, in caesium (Cs), the outermost valence electron is in the shell with energy level 6, so an electron in caesium can have an n value from 1 to 6.
For particles in a time-independent potential (see Schrödinger equation), it also labels the nth eigenvalue of Hamiltonian (H), that is, the energy E, with the contribution due to angular momentum (the term involving J2) left out. So this number depends only on the distance between the electron and the nucleus (that is, the radial coordinate r). The average distance increases with n. Hence quantum states with different principal quantum numbers are said to belong to different shells.
Azimuthal quantum number
The azimuthal quantum number, also known as the angular momentum quantum number or orbital quantum number, describes the subshell, and gives the magnitude of the orbital angular momentum through the relation.
- L2 = ħ2 ℓ (ℓ + 1)
In chemistry and spectroscopy, ℓ = 0 is called s orbital, ℓ = 1, p orbital, ℓ = 2, d orbital, and ℓ = 3, f orbital.
The value of ℓ ranges from 0 to n − 1, so the first p orbital (ℓ = 1) appears in the second electron shell (n = 2), the first d orbital (ℓ = 2) appears in the third shell (n = 3), and so on:[2]
- ℓ = 0, 1, 2,..., n − 1
A quantum number beginning in n = 3,ℓ = 0, describes an electron in the s orbital of the third electron shell of an atom. In chemistry, this quantum number is very important, since it specifies the shape of an atomic orbital and strongly influences chemical bonds and bond angles. The azimuthal quantum number can also denote the number of angular nodes present in an orbital. For example, for p orbitals, ℓ = 1 and thus the amount of angular nodes in a p orbital is 1.
Shape of orbital is also given by azimuthal quantum number.
Magnetic quantum number
The magnetic quantum number describes the specific orbital (or "cloud") within that subshell, and yields the projection of the orbital angular momentum along a specified axis:
- Lz = mℓ ħ
The s subshell (ℓ = 0) contains only one orbital, and therefore the mℓ of an electron in an s orbital will always be 0. The p subshell (ℓ = 1) contains three orbitals (in some systems, depicted as three "dumbbell-shaped" clouds), so the mℓ of an electron in a p orbital will be −1, 0, or 1. The d subshell (ℓ = 2) contains five orbitals, with mℓ values of −2, −1, 0, 1, and 2.
Spin quantum number
The spin quantum number describes the intrinsic spin angular momentum of the electron within each orbital and gives the projection of the spin angular momentum S along the specified axis:
- Sz = ms ħ.
In general, the values of ms range from −s to s, where s is the spin quantum number, associated with the particle's intrinsic spin angular momentum:[3]
- ms = −s, −s + 1, −s + 2, ..., s − 2, s − 1, s.
An electron has spin number s = 1/2, consequently ms will be ±1/2, referring to "spin up" and "spin down" states. Each electron in any individual orbital must have different quantum numbers because of the Pauli exclusion principle, therefore an orbital never contains more than two electrons.
Rules
There are no universal fixed values for mℓ and ms. Rather, the mℓ and ms values are arbitrary. The only restrictions on the choices for these constants is that the naming schematic used within a particular set of calculations or descriptions must be consistent (e.g. the orbital occupied by the first electron in a p orbital could be described as mℓ = −1 or mℓ = 0 or mℓ = 1, but the mℓ value of the next unpaired electron in that orbital must be different; yet, the mℓ assigned to electrons in other orbitals again can be mℓ = −1 or mℓ = 0 or mℓ = 1).
These rules are summarized as follows:
Name Symbol Meaning Range of values Value examples Principal quantum number n shell 1 ≤ n n = 1, 2, 3, … Azimuthal quantum number (angular momentum) ℓ subshell (s orbital is listed as 0, p orbital as 1 etc.) 0 ≤ ℓ ≤ n − 1 for n = 3:
ℓ = 0, 1, 2 (s, p, d)Magnetic quantum number (projection of angular momentum) mℓ Orbital (orientation of the orbital) −ℓ ≤ mℓ ≤ ℓ for ℓ = 2:
mℓ = −2, −1, 0, 1, 2Spin quantum number ms spin of the electron (−1/2 = "spin down", 1/2 = "spin up") −s ≤ ms ≤ s for an electron s = 1/2,
so ms = −1/2, +1/2
Example: The quantum numbers used to refer to the outermost valence electrons of a carbon (C) atom, which are located in the 2p atomic orbital, are; n = 2 (2nd electron shell), ℓ = 1 (p orbital subshell), mℓ = 1, 0, −1, ms = 1/2 (parallel spins).
Results from spectroscopy indicated that up to two electrons can occupy a single orbital. However two electrons can never have the same exact quantum state nor the same set of quantum numbers according to Hund's rules, which addresses the Pauli exclusion principle. A fourth quantum number, which represented spin with two possible values, was added as an ad hoc assumption to resolve the conflict; this supposition would later be explained in detail by relativistic quantum mechanics and from the results of the renowned Stern–Gerlach experiment.
Background
Many different models have been proposed throughout the history of quantum mechanics, but the most prominent system of nomenclature spawned from the Hund-Mulliken molecular orbital theory of Friedrich Hund, Robert S. Mulliken, and contributions from Schrödinger, Slater and John Lennard-Jones. This system of nomenclature incorporated Bohr energy levels, Hund-Mulliken orbital theory, and observations on electron spin based on spectroscopy and Hund's rules.[4]
Total angular momenta numbers
Total angular momentum of a particle
When one takes the spin–orbit interaction into consideration, the L and S operators no longer commute with the Hamiltonian, and their eigenvalues therefore change over time. Thus another set of quantum numbers should be used. This set includes[5][6]
- The total angular momentum quantum number:
- j = |ℓ ± s|
which gives the total angular momentum through the relation
- J2 = ħ2 j (j + 1)
- The projection of the total angular momentum along a specified axis:
- mj = −j, −j + 1, −j + 2, ..., j − 2, j − 1, j
analogous to the above and satisfies
- mj = mℓ + ms and |mℓ + ms| ≤ j
- Parity
This is the eigenvalue under reflection: positive (+1) for states which came from even ℓ and negative (−1) for states which came from odd ℓ. The former is also known as even parity and the latter as odd parity, and is given by
- P = (−1)ℓ
For example, consider the following 8 states, defined by their quantum numbers:
n ℓ mℓ ms ℓ + s ℓ − s mℓ + ms (1) 2 1 1 +1/2 3/2 1/23/2 (2) 2 1 1 −1/2 3/2 1/2 1/2 (3) 2 1 0 +1/2 3/2 1/2 1/2 (4) 2 1 0 −1/2 3/2 1/2 −1/2 (5) 2 1 −1 +1/2 3/2 1/2 −1/2 (6) 2 1 −1 −1/2 3/2 1/2−3/2 (7) 2 0 0 +1/2 1/2 −1/2 1/2 (8) 2 0 0 −1/2 1/2 −1/2 −1/2
The quantum states in the system can be described as linear combination of these 8 states. However, in the presence of spin–orbit interaction, if one wants to describe the same system by 8 states that are eigenvectors of the Hamiltonian (i.e. each represents a state that does not mix with others over time), we should consider the following 8 states:
j mj parity 3/2 3/2 odd coming from state (1) above 3/2 1/2 odd coming from states (2) and (3) above 3/2 −1/2 odd coming from states (4) and (5) above 3/2 −3/2 odd coming from state (6) above 1/2 1/2 odd coming from states (2) and (3) above 1/2 −1/2 odd coming from states (4) and (5) above 1/2 1/2 even coming from state (7) above 1/2 −1/2 even coming from state (8) above
Nuclear angular momentum quantum numbers
In nuclei, the entire assembly of protons and neutrons (nucleons) has a resultant angular momentum due to the angular momenta of each nucleon, usually denoted I. If the total angular momentum of a neutron is jn = ℓ + s and for a proton is jp = ℓ + s (where s for protons and neutrons happens to be 1/2 again (see note)), then the nuclear angular momentum quantum numbers I are given by:
- I = |jn − jp|, |jn − jp| + 1, |jn − jp| + 2, ..., (jn + jp) − 2, (jn + jp) − 1, (jn + jp)
Note: The orbital angular momenta of the nuclear (and atomic) states are all integer multiples of ħ while the intrinsic angular momentum of the neutron and proton are half-integer multiples. It should be immediately apparent that the combination of the intrinsic spins of the nucleons with their orbital motion will always give half-integer values for the total spin, I, of any odd-A nucleus and integer values for any even-A nucleus.
Parity with the number I is used to label nuclear angular momentum states, examples for some isotopes of hydrogen (H), carbon (C), and sodium (Na) are;[7]
11H I = (1/2)+ 96C I = (3/2)− 2011Na I = 2+ 21H I = 1+ 106C I = 0+ 2111Na I = (3/2)+ 31H I = (1/2)+ 116C I = (3/2)− 2211Na I = 3+ 126C I = 0+ 2311Na I = (3/2)+ 136C I = (1/2)− 2411Na I = 4+ 146C I = 0+ 2511Na I = (5/2)+ 156C I = (1/2)+ 2611Na I = 3+
The reason for the unusual fluctuations in I, even by differences of just one nucleon, are due to the odd and even numbers of protons and neutrons – pairs of nucleons have a total angular momentum of zero (just like electrons in orbitals), leaving an odd or even number of unpaired nucleons. The property of nuclear spin is an important factor for the operation of NMR spectroscopy in organic chemistry,[6] and MRI in nuclear medicine,[7] due to the nuclear magnetic moment interacting with an external magnetic field.
Elementary particles
Elementary particles contain many quantum numbers which are usually said to be intrinsic to them. However, it should be understood that the elementary particles are quantum states of the standard model of particle physics, and hence the quantum numbers of these particles bear the same relation to the Hamiltonian of this model as the quantum numbers of the Bohr atom does to its Hamiltonian. In other words, each quantum number denotes a symmetry of the problem. It is more useful in quantum field theory to distinguish between spacetime and internal symmetries.
Typical quantum numbers related to spacetime symmetries are spin (related to rotational symmetry), the parity, C-parity and T-parity (related to the Poincaré symmetry of spacetime). Typical internal symmetries[clarification needed] are lepton number and baryon number or the electric charge. (For a full list of quantum numbers of this kind see the article on flavour.)
Multiplicative quantum numbers
Most conserved quantum numbers are additive, so in an elementary particle reaction, the sum of the quantum numbers should be the same before and after the reaction. However, some, usually called a parity, are multiplicative; i.e., their product is conserved. All multiplicative quantum numbers belong to a symmetry (like parity) in which applying the symmetry transformation twice is equivalent to doing nothing (involution).
See also
Notes
- ↑ specifically, observables [math]\displaystyle{ \widehat{A} }[/math] that commute with the Hamiltonian are simultaneously diagonalizable with it and so the eigenvalues [math]\displaystyle{ a }[/math] and the energy (eigenvalues of the Hamiltonian) are not limited by an uncertainty relation arising from non-commutativity.
- ↑ Many observables have discrete spectra (sets of eigenvalues) in quantum mechanics, so the quantities can only be measured in discrete (often integer) values.
References
- ↑ Beiser, A. (1987). Concepts of Modern Physics (4th ed.). McGraw-Hill (International). ISBN 0-07-100144-1.[page needed]
- ↑ Atkins, P. W. (1977). Molecular Quantum Mechanics Parts I and II: An Introduction to Quantum Chemistry. 1. Oxford University Press. ISBN 0-19-855129-0.
- ↑ Peleg, Y.; Pnini, R.; Zaarur, E.; Hecht, E. (2010). Quantum Mechanics. Schuam's Outlines (2nd ed.). McGraw Hill (USA). ISBN 978-0-07-162358-2.[page needed]
- ↑ Chemistry, Matter, and the Universe, R.E. Dickerson, I. Geis, W.A. Benjamin Inc. (USA), 1976, ISBN:0-19-855148-7
- ↑ Atkins, P. W. (1977). Molecular Quantum Mechanics Parts I and II: An Introduction to Quantum Chemistry. 1. Oxford University Press. ISBN 0-19-855129-0.[page needed]
- ↑ 6.0 6.1 Atkins, P. W. (1977). Molecular Quantum Mechanics Part III: An Introduction to Quantum Chemistry. 2. Oxford University Press.[ISBN missing][page needed]
- ↑ 7.0 7.1 Krane, K. S. (1988). Introductory Nuclear Physics. John Wiley & Sons. ISBN 978-0-471-80553-3.[page needed]
Further reading
- Dirac, Paul A. M. (1982). Principles of quantum mechanics. Oxford University Press. ISBN 0-19-852011-5.
- Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. ISBN 0-13-805326-X. https://archive.org/details/introductiontoel00grif_0.
- Halzen, Francis; Martin, Alan D. (1984). QUARKS AND LEPTONS: An Introductory Course in Modern Particle Physics. John Wiley & Sons. ISBN 0-471-88741-2. https://archive.org/details/quarksleptonsint0000halz.
- Eisberg, Robert Martin; Resnick, Robert (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles (2nd ed.). John Wiley & Sons. ISBN 978-0-471-87373-0. https://archive.org/details/quantumphysicsof00eisb.
External links
 |  |
EncycloReader
is supported by the 
KSF