Table of Contents Categories
  Encyclosphere.org ENCYCLOREADER
  supported by EncyclosphereKSF

SQUID

Topic: Physics

 From HandWiki - Reading time: 10 min
Short description: Type of magnetometer
Sensing element of a SQUID, 2008

A SQUID (superconducting quantum interference device) is a very sensitive magnetometer used to measure extremely weak magnetic fields, based on superconducting loops containing Josephson junctions.

SQUIDs are sensitive enough to measure fields as low as 5×10−14 T with a few days of averaged measurements.[1] Their noise levels are as low as 3 fT·Hz−​1⁄2.[2] For comparison, a typical refrigerator magnet produces 0.01 tesla (10−2 T), and some processes in animals produce very small magnetic fields between 10−9 T and 10−6 T. SERF atomic magnetometers, invented in the early 2000s are potentially more sensitive and do not require cryogenic refrigeration but are orders of magnitude larger in size (~1 cm3) and must be operated in a near-zero magnetic field.

History and design

There are two main types of SQUID: direct current (DC) and radio frequency (RF). RF SQUIDs can work with only one Josephson junction (superconducting tunnel junction), which might make them cheaper to produce, but are less sensitive.

DC SQUID

Diagram of a DC SQUID. The current [math]\displaystyle{ I }[/math] enters and splits into the two paths, each with currents [math]\displaystyle{ I_a }[/math] and [math]\displaystyle{ I_b }[/math]. The thin barriers on each path are Josephson junctions, which together separate the two superconducting regions. [math]\displaystyle{ \Phi }[/math] represents the magnetic flux threading the DC SQUID loop.
Electrical schematic of a SQUID where [math]\displaystyle{ I_b }[/math] is the bias current, [math]\displaystyle{ I_0 }[/math] is the critical current of the SQUID, [math]\displaystyle{ \Phi }[/math] is the flux threading the SQUID and [math]\displaystyle{ V }[/math] is the voltage response to that flux. The X-symbols represent Josephson junctions.
Left: Plot of current vs. voltage for a SQUID. Upper and lower curves correspond to [math]\displaystyle{ n \cdot \Phi_0 }[/math] and [math]\displaystyle{ n+\frac{1}{2} \cdot \Phi_0 }[/math] respectively. Right: Periodic voltage response due to flux through a SQUID. The periodicity is equal to one flux quantum, [math]\displaystyle{ \Phi_0 }[/math].

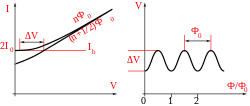
The DC SQUID was invented in 1964 by Robert Jaklevic, John J. Lambe, James Mercereau, and Arnold Silver of Ford Research Labs[3] after Brian Josephson postulated the Josephson effect in 1962, and the first Josephson junction was made by John Rowell and Philip Anderson at Bell Labs in 1963.[4] It has two Josephson junctions in parallel in a superconducting loop. It is based on the DC Josephson effect. In the absence of any external magnetic field, the input current [math]\displaystyle{ I }[/math] splits into the two branches equally. If a small external magnetic field is applied to the superconducting loop, a screening current, [math]\displaystyle{ I_s }[/math], begins to circulate the loop that generates the magnetic field canceling the applied external flux, and creates an additional Josephson phase which is proportional to this external magnetic flux.[5] The induced current is in the same direction as [math]\displaystyle{ I }[/math] in one of the branches of the superconducting loop, and is opposite to [math]\displaystyle{ I }[/math] in the other branch; the total current becomes [math]\displaystyle{ I/2 + I_s }[/math] in one branch and [math]\displaystyle{ I/2 - I_s }[/math] in the other. As soon as the current in either branch exceeds the critical current, [math]\displaystyle{ I_c }[/math], of the Josephson junction, a voltage appears across the junction.

Now suppose the external flux is further increased until it exceeds [math]\displaystyle{ \Phi_0/2 }[/math], half the magnetic flux quantum. Since the flux enclosed by the superconducting loop must be an integer number of flux quanta, instead of screening the flux the SQUID now energetically prefers to increase it to [math]\displaystyle{ \Phi_0 }[/math]. The current now flows in the opposite direction, opposing the difference between the admitted flux [math]\displaystyle{ \Phi_0 }[/math] and the external field of just over [math]\displaystyle{ \Phi_0/2 }[/math]. The current decreases as the external field is increased, is zero when the flux is exactly [math]\displaystyle{ \Phi_0 }[/math], and again reverses direction as the external field is further increased. Thus, the current changes direction periodically, every time the flux increases by additional half-integer multiple of [math]\displaystyle{ \Phi_0 }[/math], with a change at maximum amperage every half-plus-integer multiple of [math]\displaystyle{ \Phi_0 }[/math] and at zero amps every integer multiple.

If the input current is more than [math]\displaystyle{ I_c }[/math], then the SQUID always operates in the resistive mode. The voltage, in this case, is thus a function of the applied magnetic field and the period equal to [math]\displaystyle{ \Phi_0 }[/math]. Since the current-voltage characteristic of the DC SQUID is hysteretic, a shunt resistance, [math]\displaystyle{ R }[/math] is connected across the junction to eliminate the hysteresis (in the case of copper oxide based high-temperature superconductors the junction's own intrinsic resistance is usually sufficient). The screening current is the applied flux divided by the self-inductance of the ring. Thus [math]\displaystyle{ \Delta \Phi }[/math] can be estimated as the function of [math]\displaystyle{ \Delta V }[/math] (flux to voltage converter)[6][7] as follows:

[math]\displaystyle{ \Delta V = R \cdot \Delta I }[/math]
[math]\displaystyle{ 2 \cdot \Delta I = 2 \cdot \frac{\Delta \Phi}{L} }[/math], where [math]\displaystyle{ L }[/math] is the self inductance of the superconducting ring
[math]\displaystyle{ \Delta V = \frac{R}{L} \cdot \Delta \Phi }[/math]

The discussion in this section assumed perfect flux quantization in the loop. However, this is only true for big loops with a large self-inductance. According to the relations, given above, this implies also small current and voltage variations. In practice the self-inductance [math]\displaystyle{ L }[/math] of the loop is not so large. The general case can be evaluated by introducing a parameter

[math]\displaystyle{ \lambda = \frac{i_cL}{\Phi_0} }[/math]

where [math]\displaystyle{ i_c }[/math] is the critical current of the SQUID. Usually [math]\displaystyle{ \lambda }[/math] is of order one.[8]

RF SQUID

A prototype SQUID

The RF SQUID was invented in 1965 by Robert Jaklevic, John J. Lambe, Arnold Silver, and James Edward Zimmerman at Ford.[7] It is based on the AC Josephson effect and uses only one Josephson junction. It is less sensitive compared to DC SQUID but is cheaper and easier to manufacture in smaller quantities. Most fundamental measurements in biomagnetism, even of extremely small signals, have been made using RF SQUIDS.[9][10] The RF SQUID is inductively coupled to a resonant tank circuit.[11] Depending on the external magnetic field, as the SQUID operates in the resistive mode, the effective inductance of the tank circuit changes, thus changing the resonant frequency of the tank circuit. These frequency measurements can be easily taken, and thus the losses which appear as the voltage across the load resistor in the circuit are a periodic function of the applied magnetic flux with a period of [math]\displaystyle{ \Phi_0 }[/math]. For a precise mathematical description refer to the original paper by Erné et al.[6][12]

Materials used

The traditional superconducting materials for SQUIDs are pure niobium or a lead alloy with 10% gold or indium, as pure lead is unstable when its temperature is repeatedly changed. To maintain superconductivity, the entire device needs to operate within a few degrees of absolute zero, cooled with liquid helium.[13]

High-temperature SQUID sensors were developed in the late 1980s.[14] They are made of high-temperature superconductors, particularly YBCO, and are cooled by liquid nitrogen which is cheaper and more easily handled than liquid helium. They are less sensitive than conventional low temperature SQUIDs but good enough for many applications.[15]

In 2006, A proof of concept was shown for CNT-SQUID sensors built with an aluminium loop and a single walled carbon nanotube Josephson junction.[16] The sensors are a few 100 nm in size and operate at 1K or below. Such sensors allow to count spins.[17]

In 2022 a SQUID was constructed on magic angle twisted bilayer graphene (MATBG)[18][19]

Uses

The inner workings of an early SQUID, circa 1990

The extreme sensitivity of SQUIDs makes them ideal for studies in biology. Magnetoencephalography (MEG), for example, uses measurements from an array of SQUIDs to make inferences about neural activity inside brains. Because SQUIDs can operate at acquisition rates much higher than the highest temporal frequency of interest in the signals emitted by the brain (kHz), MEG achieves good temporal resolution. Another area where SQUIDs are used is magnetogastrography, which is concerned with recording the weak magnetic fields of the stomach. A novel application of SQUIDs is the magnetic marker monitoring method, which is used to trace the path of orally applied drugs. In the clinical environment SQUIDs are used in cardiology for magnetic field imaging (MFI), which detects the magnetic field of the heart for diagnosis and risk stratification.

Probably the most common commercial use of SQUIDs is in magnetic property measurement systems (MPMS). These are turn-key systems, made by several manufacturers, that measure the magnetic properties of a material sample. This is typically done over a temperature range from that of 300 mK to roughly 400 K.[20] With the decreasing size of SQUID sensors since the last decade, such sensor can equip the tip of an AFM probe. Such device allows simultaneous measurement of roughness of the surface of a sample and the local magnetic flux.[21]

For example, SQUIDs are being used as detectors to perform magnetic resonance imaging (MRI). While high-field MRI uses precession fields of one to several teslas, SQUID-detected MRI uses measurement fields that lie in the microtesla range. In a conventional MRI system, the signal scales as the square of the measurement frequency (and hence precession field): one power of frequency comes from the thermal polarization of the spins at ambient temperature, while the second power of field comes from the fact that the induced voltage in the pickup coil is proportional to the frequency of the precessing magnetization. In the case of untuned SQUID detection of prepolarized spins, however, the NMR signal strength is independent of precession field, allowing MRI signal detection in extremely weak fields, on the order of Earth's magnetic field. SQUID-detected MRI has advantages over high-field MRI systems, such as the low cost required to build such a system, and its compactness. The principle has been demonstrated by imaging human extremities, and its future application may include tumor screening.[22]

Another application is the scanning SQUID microscope, which uses a SQUID immersed in liquid helium as the probe. The use of SQUIDs in oil prospecting, mineral exploration,[23] earthquake prediction and geothermal energy surveying is becoming more widespread as superconductor technology develops; they are also used as precision movement sensors in a variety of scientific applications, such as the detection of gravitational waves.[24] A SQUID is the sensor in each of the four gyroscopes employed on Gravity Probe B in order to test the limits of the theory of general relativity.[1]

A modified RF SQUID was used to observe the dynamical Casimir effect for the first time.[25][26]

SQUIDs constructed from super-cooled niobium wire loops are used as the basis for D-Wave Systems 2000Q quantum computer.[27]

Transition-edge sensors

One of the largest uses of SQUIDs is to read out superconducting Transition-edge sensors. Hundreds of thousands of multiplexed SQUIDs coupled to transition-edge sensors are presently being deployed to study the Cosmic microwave background, for X-ray astronomy, to search for dark matter made up of Weakly interacting massive particles, and for spectroscopy at Synchrotron light sources.

Cold dark matter

Advanced SQUIDS called near quantum-limited SQUID amplifiers form the basis of the Axion Dark Matter Experiment (ADMX) at the University of Washington. Axions are a prime candidate for cold dark matter.[28]

Proposed uses

A potential military application exists for use in anti-submarine warfare as a magnetic anomaly detector (MAD) fitted to maritime patrol aircraft.[29]

SQUIDs are used in superparamagnetic relaxometry (SPMR), a technology that utilizes the high magnetic field sensitivity of SQUID sensors and the superparamagnetic properties of magnetite nanoparticles.[30][31] These nanoparticles are paramagnetic; they have no magnetic moment until exposed to an external field where they become ferromagnetic. After removal of the magnetizing field, the nanoparticles decay from a ferromagnetic state to a paramagnetic state, with a time constant that depends upon the particle size and whether they are bound to an external surface. Measurement of the decaying magnetic field by SQUID sensors is used to detect and localize the nanoparticles. Applications for SPMR may include cancer detection.[32]

See also

Notes

  1. ↑ 1.0 1.1 Ran, Shannon K’doah (2004). Gravity Probe B: Exploring Einstein's Universe with Gyroscopes. NASA. p. 26. http://einstein.stanford.edu/content/education/GP-B_T-Guide4-2008.pdf. 
  2. ↑ D. Drung; C. Assmann; J. Beyer; A. Kirste; M. Peters; F. Ruede; Th. Schurig (2007). "Highly sensitive and easy-to-use SQUID sensors". IEEE Transactions on Applied Superconductivity 17 (2): 699–704. doi:10.1109/TASC.2007.897403. Bibcode: 2007ITAS...17..699D. http://ib.ptb.de/de/org/7/75/751/SQUID_Stromsensoren/Drung_ASC06_Preprint.pdf. 
  3. ↑ R. C. Jaklevic; J. Lambe; A. H. Silver; J. E. Mercereau (1964). "Quantum Interference Effects in Josephson Tunneling". Physical Review Letters 12 (7): 159–160. doi:10.1103/PhysRevLett.12.159. Bibcode: 1964PhRvL..12..159J. 
  4. ↑ Anderson, P.; Rowell, J. (1963). "Probable Observation of the Josephson Superconducting Tunneling Effect". Physical Review Letters 10 (6): 230–232. doi:10.1103/PhysRevLett.10.230. Bibcode: 1963PhRvL..10..230A. 
  5. ↑ "The Feynman Lectures on Physics Vol. III Ch. 21: The Schrödinger Equation in a Classical Context: A Seminar on Superconductivity, Section 21–9: The Josephson junction". https://feynmanlectures.caltech.edu/III_21.html. 
  6. ↑ 6.0 6.1 E. du Trémolet de Lacheisserie, D. Gignoux, and M. Schlenker (editors) (2005). Magnetism: Materials and Applications. 2. Springer. 
  7. ↑ 7.0 7.1 J. Clarke and A. I. Braginski (Eds.) (2004). The SQUID handbook. 1. Wiley-Vch. 
  8. ↑ A.TH.A.M. de Waele; R. de Bruyn Ouboter (1969). "Quantum-interference phenomena in point contacts between two superconductors". Physica 41 (2): 225–254. doi:10.1016/0031-8914(69)90116-5. Bibcode: 1969Phy....41..225D. 
  9. ↑ Romani, G. L.; Williamson, S. J.; Kaufman, L. (1982). "Biomagnetic instrumentation". Review of Scientific Instruments 53 (12): 1815–1845. doi:10.1063/1.1136907. PMID 6760371. Bibcode: 1982RScI...53.1815R. 
  10. ↑ Sternickel, K.; Braginski, A. I. (2006). "Biomagnetism using SQUIDs: Status and perspectives". Superconductor Science and Technology 19 (3): S160. doi:10.1088/0953-2048/19/3/024. Bibcode: 2006SuScT..19S.160S. 
  11. ↑ Nisenoff, M.; Wolf, S. (1975-09-01). "Observation of a $cos\ensuremath{\varphi}$ term in the current-phase relation for "Dayem"-type weak link contained in an rf-biased superconducting quantum interference device". Physical Review B 12 (5): 1712–1714. doi:10.1103/PhysRevB.12.1712. 
  12. ↑ S.N. Erné; H.-D. Hahlbohm; H. Lübbig (1976). "Theory of the RF biased Superconducting Quantum Interference Device for the non-hysteretic regime". J. Appl. Phys. 47 (12): 5440–5442. doi:10.1063/1.322574. Bibcode: 1976JAP....47.5440E. 
  13. ↑ Clarke, John (August 1994). "SQUIDs". Scientific American 271 (2): 46–53. doi:10.1038/scientificamerican0894-46. Bibcode: 1994SciAm.271b..46C. https://www.jstor.org/stable/24942801. Retrieved 18 August 2022. 
  14. ↑ M.S. Colclough, C.E. Gough et al, Radiofrequency SQUID operation usinga ceramic high temperature superconductor, Nature 328, 47 (1987)
  15. ↑ LP Lee et al., Monolithic 77K DC SQUID magnetometer, Applied Physics Letters 59, 3051 (1991)
  16. ↑ Cleuziou, J.-P.; Wernsdorfer, W. (2006). "Carbon nanotube superconducting quantum interference device". Nature Nanotechnology 1 (October): 53–59. doi:10.1038/nnano.2006.54. PMID 18654142. Bibcode: 2006NatNa...1...53C. 
  17. ↑ Aprili, Marco (2006). "The nanoSQUID makes its debut". Nature Nanotechnology 1 (October): 15–16. doi:10.1038/nnano.2006.78. PMID 18654132. Bibcode: 2006NatNa...1...15A. 
  18. ↑ Portolés, Elías; Iwakiri, Shuichi; Zheng, Giulia; Rickhaus, Peter; Taniguchi, Takashi; Watanabe, Kenji; Ihn, Thomas; Ensslin, Klaus et al. (24 October 2022). "A tunable monolithic SQUID in twisted bilayer graphene" (in en). Nature Nanotechnology 17 (11): 1159–1164. doi:10.1038/s41565-022-01222-0. ISSN 1748-3395. PMID 36280761. Bibcode: 2022NatNa..17.1159P. https://www.nature.com/articles/s41565-022-01222-0. 
  19. ↑ "A new quantum component made from graphene" (in en). 3 November 2022. https://ethz.ch/en/news-and-events/eth-news/news/2022/11/a-new-quantum-component-made-from-graphene.html. 
  20. ↑ Kleiner, R.; Koelle, D.; Ludwig, F.; Clarke, J. (2004). "Superconducting quantum interference devices: State of the art and applications". Proceedings of the IEEE 92 (10): 1534–1548. doi:10.1109/JPROC.2004.833655. 
  21. ↑ "Microscopie à microsquid - Institut NÉEL". http://neel.cnrs.fr/spip.php?article914&lang=en. 
  22. ↑ Clarke, J.; Lee, A.T.; Mück, M.; Richards, P.L.. "Chapter 8.3". Nuclear Magnetic and Quadrupole Resonance and Magnetic Resonance Imaging. pp. 56–81.  in Clarke & Braginski 2006
  23. ↑ P. Schmidt; D. Clark; K. Leslie; M. Bick; D. Tilbrook; C. Foley (2004). "GETMAG—A SQUID magnetic tensor gradiometer for mineral and oil exploration". Exploration Geophysics 35 (4): 297–305. doi:10.1071/eg04297. 
  24. ↑ Paik, Ho J.. "Chapter 15.2". "Superconducting Transducer for Gravitational-Wave Detectors" in [volume 2 of] "The SQUID Handbook: Applications of SQUIDs and SQUID Systems". pp. 548–554.  in Clarke & Braginski 2006
  25. ↑ "First Observation of the Dynamical Casimir Effect". Technology Review. http://www.technologyreview.com/blog/arxiv/26813/. 
  26. ↑ Wilson, C. M. (2011). "Observation of the Dynamical Casimir Effect in a Superconducting Circuit". Nature 479 (7373): 376–379. doi:10.1038/nature10561. PMID 22094697. Bibcode: 2011Natur.479..376W. 
  27. ↑ "Not Magic Quantum". July 2016. http://www.lanl.gov/discover/publications/1663/2016-july/_assets/docs/1663_JULY-2016-Not-Magic-Quantum.pdf. Retrieved 2021-10-26. 
  28. ↑ A Squid-Based Microwave Cavity Search For Axions By ADMX; SJ Sztalos, G Carlos, C Hagman, D Kinion, K van Bibber, M Hotz, L Rosenberg, G Rybka, J Hoskins, J Hwang, P Sikivie, DB Tanner, R Bradley, J Clarke; Phys.Rev.Lett. 104:041301; 2010
  29. ↑ Ouellette, Jennifer. "SQUID Sensors Penetrate New Markets". The Industrial Physicist. p. 22. http://www.aip.org/tip/INPHFA/vol-4/iss-2/p20.pdf. 
  30. ↑ Flynn, E R; Bryant, H C (2005). "A biomagnetic system for in vivo cancer imaging". Physics in Medicine and Biology 50 (6): 1273–1293. doi:10.1088/0031-9155/50/6/016. PMID 15798322. Bibcode: 2005PMB....50.1273F. 
  31. ↑ De Haro, Leyma P.; Karaulanov, Todor; Vreeland, Erika C.; Anderson, Bill; Hathaway, Helen J.; Huber, Dale L.; Matlashov, Andrei N.; Nettles, Christopher P. et al. (2015-10-01). "Magnetic relaxometry as applied to sensitive cancer detection and localization". Biomedical Engineering / Biomedizinische Technik 60 (5): 445–455. doi:10.1515/bmt-2015-0053. ISSN 1862-278X. PMID 26035107. https://www.osti.gov/biblio/1227725. 
  32. ↑ Hathaway, Helen J.; Butler, Kimberly S.; Adolphi, Natalie L.; Lovato, Debbie M.; Belfon, Robert; Fegan, Danielle; Monson, Todd C.; Trujillo, Jason E. et al. (2011-01-01). "Detection of breast cancer cells using targeted magnetic nanoparticles and ultra-sensitive magnetic field sensors". Breast Cancer Research 13 (5): R108. doi:10.1186/bcr3050. ISSN 1465-542X. PMID 22035507. 

References

  • Clarke, John; Braginski, Alex I., eds (2006). The SQUID Handbook: Applications of SQUIDs and SQUID Systems. 2. Wiley-VCH. ISBN 978-3-527-40408-7. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:SQUID&oldid=3278569"
Licensed under CC BY-SA 3.0 | Source: https://handwiki.org/wiki/Physics:SQUID
11 views | Status: cached on July 31 2024 08:09:06
↧ Download this article as ZWI file
Encyclosphere.org EncycloReader is supported by the EncyclosphereKSF