Spice (oceanography)

Spice, spiciness, or spicity, symbol τ, is a term in oceanography referring to variations in the temperature and salinity of seawater over space or time, whose combined effects leave the water's density unchanged. For a given spice, any change in temperature is offset by a change in salinity to maintain unchanged density. An increase in temperature decreases density, but an increase in salinity increases density. Such density-compensated thermohaline variability is ubiquitous in the upper ocean. Warmer, saltier water is more spicy while cooler, less salty water is more minty.^[1] For a density ratio of 1, all the thermohaline variability is spice, and there are no density fluctuations.

Mathematical description

The density of seawater controls much of the movement of water, or the thermohaline flow, in the ocean. The density of seawater is primarily determined by the temperature and salinity of that water. Changes in these two main parameters, potential temperature Θ and salinity S, are multiplied with their thermal expansion [math]\displaystyle{ \alpha }[/math] or haline contraction coefficient [math]\displaystyle{ \beta }[/math] equal to each other; [math]\displaystyle{ \alpha d\Theta }[/math] and [math]\displaystyle{ \beta dS }[/math] are both proportional to a change in density and are both terms of the linearized equation of state of the ocean (TEOS-10). This similarity is supposed to be relevant for understanding the consequences of sea water mixing.^[2]

[math]\displaystyle{ \alpha d\Theta=\beta dS }[/math]

The density [math]\displaystyle{ \rho }[/math] doesn't change over an isopycnal. However, by mixing a change in temperature and salinity can occur. Therefore spiciness [math]\displaystyle{ \tau }[/math] is introduced as variable that is proportional to thermal expansion and haline contraction. Integration of this variable along an isopycnal leads to the following equation.

[math]\displaystyle{ \int_\rho d\tau=\int_\rho \alpha d\Theta=\int_\rho \beta dS }[/math]

Spiciness could be described as the isothermal gradient of the density that equals the isohaline gradient of the density.

[math]\displaystyle{ \tau=2\int\frac{d\rho}{dS}|_\Theta \quad dS=-2 \int \frac{d\rho}{d\Theta}|_S \,d\Theta }[/math]

The isopycnal gradient of spiciness should equal to the isopycnal gradient of temperature and salinity by multiplication with the derivative in the other variable of the density.

[math]\displaystyle{ d\tau |_\rho=2\rho_S dS |_\rho=-2\rho_\Theta d\Theta |_\rho }[/math]

Another mathematical implication for the existence of a spiciness influence manifests itself in a [math]\displaystyle{ S,\Theta }[/math]-diagram, where the negative slope of the isopleths equals the ratio between the temperature- and salinity derivative of the spiciness.^[3]

[math]\displaystyle{ \frac{dS}{d\Theta}|_\tau=-\frac{\tau_\Theta}{\tau_S} }[/math]

Applications

Spiciness-potential density diagram with the stable and unstable regions shown.

The spiciness and the potential density are plotted at the surface. Spiciness (variation) is especially relevant when looking at isopycnals (for example at the polar regions). Data is proveded by ^[4]

A purpose for introducing spiciness is to decrease the amount of state variables needed; the density at constant depth is a function of potential temperature and salinity and of using both, spiciness can be used. If the goal is to only quantify the variation of water parcels along isopycnals, the variation in absolute salinity or temperature can be used instead because it gives the same information with the same amount of variables.^[3]

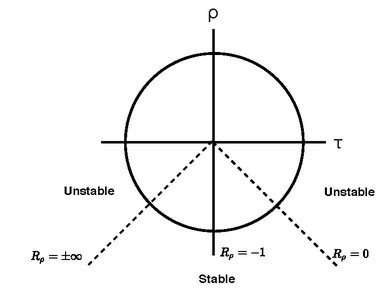
Another purpose is to examine how the stability ratio [math]\displaystyle{ R_\rho }[/math] varies vertically on a water column. The stability ratio is a number determining the involvement of temperature changes relative to the involvement salinity changes in a vertical profile, which yields relevant information about the stability of the water column:

[math]\displaystyle{ R_\rho=(-\rho_\Theta \Theta_z)/(\rho_S S_z) }[/math]

The vertical variation of this number is often shown in a spiciness-potential density diagram and/or plot, where the angle shows the stability.^[5]

Computation

The spiciness can be calculated in several programming languages with the Gibbs SeaWater (GSW) toolbox.^[6] It is used to derive thermodynamic seawater properties and is adopted by the Intergovernmental Oceanographic Commission (IOC), International Association for the Physical Sciences of the Oceans (IAPSO) and the Scientific Committee on Oceanic Research (SCOR). They use the definition of spiciness (gsw_spiciness0(), gsw_spiciness1(), gsw_spiciness2() at respectively 0, 1000 and 2000 dbar) provided by.^[7] These isobars are chosen because they correspond to commonly used potential density surfaces. Areas with constant density but different spiciness have a net water flow of heat and salinity due to diffusion.

Disagreements

The exact definition of spiciness is debated. Specifically, the orthogonality of the density with spiciness and the used scaling factor of potential temperature and salinity. McDougall^[3] claims that orthogonality should not be imposed because:

• There is no physical reason to impose orthogonality.
• Imposing orthogonality would 'necessarily depends on an arbitrary scaling factor of the salinity and temperature axes'. In other words, spiciness would have different meanings for different (chosen) scaling factors.
• The meaning of spiciness changes with density. As a result, spiciness may only be useful over small vertical extensions in the surface layer.^[5]

McDougall^[7] is adopted by the Intergovernmental Oceanographic Commission (IOC), International Association for the Physical Sciences of the Oceans (IAPSO) and the Scientific Committee on Oceanic Research (SCOR) due to their implementation of spiciness in the TEOS-10.^[6]

Huang^[8] claims that the orthogonal system is superior to the non orthogonal system because the coordinates can be regarded as independent and distances between points can be calculated more easily.

McDougall^[3] recommended that the spiciness should not be used. Instead, they recommend that the variation of salinity should be used to differentiate between isopycnal water parcels and the stability ratio [math]\displaystyle{ R_\rho }[/math] on vertical water columns for stability.

References

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Spice (oceanography). Read more