Table of Contents Categories
  Encyclosphere.org ENCYCLOREADER
  supported by EncyclosphereKSF

Surface roughness

Topic: Physics

 From HandWiki - Reading time: 15 min
Short description: Measure of surface finish or texture
The basic symbol of surface roughness
Digital holographic microscope measuring hip prosthesis roughness

Surface roughness can be regarded as the quality of a surface of not being smooth and it is hence linked to human (haptic) perception of the surface texture. From a mathematical perspective it is related to the spatial variability structure of surfaces, and inherently it is a multiscale property. It has different interpretations and definitions depending on the disciplines considered.

In surface metrology

Surface roughness, often shortened to roughness, is a component of surface finish (surface texture). It is quantified by the deviations in the direction of the normal vector of a real surface from its ideal form. If these deviations are large, the surface is rough; if they are small, the surface is smooth. In surface metrology, roughness is typically considered to be the high-frequency, short-wavelength component of a measured surface. However, in practice it is often necessary to know both the amplitude and frequency to ensure that a surface is fit for a purpose.

Roughness plays an important role in determining how a real object will interact with its environment. In tribology, rough surfaces usually wear more quickly and have higher friction coefficients than smooth surfaces. Roughness is often a good predictor of the performance of a mechanical component, since irregularities on the surface may form nucleation sites for cracks or corrosion. On the other hand, roughness may promote adhesion. Generally speaking, rather than scale specific descriptors, cross-scale descriptors such as surface fractality provide more meaningful predictions of mechanical interactions at surfaces including contact stiffness[1] and static friction.[2]

Although a high roughness value is often undesirable, it can be difficult and expensive to control in manufacturing. For example, it is difficult and expensive to control surface roughness of fused deposition modelling (FDM) manufactured parts.[3] Decreasing the roughness of a surface usually increases its manufacturing cost. This often results in a trade-off between the manufacturing cost of a component and its performance in application.

Roughness can be measured by manual comparison against a "surface roughness comparator" (a sample of known surface roughness), but more generally a surface profile measurement is made with a profilometer. These can be of the contact variety (typically a diamond stylus) or optical (e.g.: a white light interferometer or laser scanning confocal microscope).

However, controlled roughness can often be desirable. For example, a gloss surface can be too shiny to the eye and too slippery to the finger (a touchpad is a good example) so a controlled roughness is required. This is a case where both amplitude and frequency are very important.

Parameters

A roughness value can either be calculated on a profile (line) or on a surface (area). The profile roughness parameter ([math]\displaystyle{ Ra }[/math], [math]\displaystyle{ Rq }[/math], ...) are more common. The area roughness parameters ([math]\displaystyle{ Sa }[/math], [math]\displaystyle{ Sq }[/math], ...) give more significant values.

Profile roughness parameters[4]

The profile roughness parameters are included in BS EN ISO 4287:2000 British standard, identical with the ISO 4287:1997 standard.[5] The standard is based on the ″M″ (mean line) system. There are many different roughness parameters in use, but [math]\displaystyle{ Ra }[/math] is by far the most common, though this is often for historical reasons and not for particular merit, as the early roughness meters could only measure [math]\displaystyle{ Ra }[/math]. Other common parameters include [math]\displaystyle{ Rz }[/math], [math]\displaystyle{ Rq }[/math], and [math]\displaystyle{ Rsk }[/math]. Some parameters are used only in certain industries or within certain countries. For example, the [math]\displaystyle{ Rk }[/math] family of parameters is used mainly for cylinder bore linings, and the Motif parameters are used primarily in the French automotive industry.[6] The MOTIF method provides a graphical evaluation of a surface profile without filtering waviness from roughness. A motif consists of the portion of a profile between two peaks and the final combinations of these motifs eliminate ″insignificant″ peaks and retains ″significant″ ones. Please note that [math]\displaystyle{ Ra }[/math] is a dimensional unit that can be micrometer or microinch.

Since these parameters reduce all of the information in a profile to a single number, great care must be taken in applying and interpreting them. Small changes in how the raw profile data is filtered, how the mean line is calculated, and the physics of the measurement can greatly affect the calculated parameter. With modern digital equipment, the scan can be evaluated to make sure there are no obvious glitches that skew the values.

Because it may not be obvious to many users what each of the measurements really mean, a simulation tool allows a user to adjust key parameters, visualizing how surfaces which are obviously different to the human eye are differentiated by the measurements. For example, [math]\displaystyle{ Ra }[/math] fails to distinguish between two surfaces where one is composed of peaks on an otherwise smooth surface and the other is composed of troughs of the same amplitude. Such tools can be found in app format.[7]

By convention every 2D roughness parameter is a capital [math]\displaystyle{ R }[/math] followed by additional characters in the subscript. The subscript identifies the formula that was used, and the [math]\displaystyle{ R }[/math] means that the formula was applied to a 2D roughness profile. Different capital letters imply that the formula was applied to a different profile. For example, [math]\displaystyle{ Ra }[/math] is the arithmetic average of the roughness profile, [math]\displaystyle{ Pa }[/math] is the arithmetic average of the unfiltered raw profile, and [math]\displaystyle{ Sa }[/math] is the arithmetic average of the 3D roughness.

Each of the formulas listed in the tables assumes that the roughness profile has been filtered from the raw profile data and the mean line has been calculated. The roughness profile contains [math]\displaystyle{ n }[/math] ordered, equally spaced points along the trace, and [math]\displaystyle{ y_i }[/math] is the vertical distance from the mean line to the [math]\displaystyle{ i^\text{th} }[/math] data point. Height is assumed to be positive in the up direction, away from the bulk material.

Amplitude parameters

Amplitude parameters characterize the surface based on the vertical deviations of the roughness profile from the mean line. Many of them are closely related to the parameters found in statistics for characterizing population samples. For example, [math]\displaystyle{ Ra }[/math] is the arithmetic average value of filtered roughness profile determined from deviations about the center line within the evaluation length and [math]\displaystyle{ Rt }[/math] is the range of the collected roughness data points.

The arithmetic average roughness, [math]\displaystyle{ Ra }[/math], is the most widely used one-dimensional roughness parameter.

Parameter Description Formula
Ra,[8] Raa, Ryni Average, or arithmetic average of profile height deviations from the mean line.[9] [math]\displaystyle{ Ra = \frac{1}{l_r} \int_{0}^{l_r} \left| z(x) \right| dx }[/math][4][5]
Rq, Rms[8] Quadratic mean, or root mean square average of profile height deviations from the mean line.[9] [math]\displaystyle{ Rq = \sqrt{ \frac{1}{l_r} \int_{0}^{l_r} z(x)^2dx } }[/math][4][5]
Rvi; Rv Maximum valley depth below the mean line, within a single sampling length; Average Rv value over assessment length [4] [math]\displaystyle{ Rv_i = |\min z(x)| }[/math]; [math]\displaystyle{ Rv= \frac{\sum_{i=1}^n Rv_i}{n} }[/math][4]
Rpi; Rp Maximum peak height above the mean line, within a single sampling length; Average Rp value over assessment length[4] [math]\displaystyle{ Rp_i = \max z(x) }[/math]; [math]\displaystyle{ Rp= \frac{\sum_{i=1}^n Rp_i}{n} }[/math][4]
Rzi; Rz Maximum peak to valley height of the profile, within a single sampling length; Average Rz value over assessment length[4] [math]\displaystyle{ Rz_i = Rp_i + Rv_i }[/math];[4] [math]\displaystyle{ Rz= \frac{\sum_{i=1}^n Rz_i}{n} }[/math]
Rsk Skewness, or measure of asymmetry of the profile about the mean line.[9] [math]\displaystyle{ Rsk = \frac{1}{Rq^3} \left[\frac{1}{l_r}\int_{0}^{l_r} Z^3(x)dx\right] }[/math][5]
Rku Kurtosis, or measure of peakedness (or tailedness) of the profile about the mean line.[9] [math]\displaystyle{ Rku = \frac 1{{R_q}^4}\left[\frac1{l_r}\int_0^{l_r}Z^4(x)dx\right] }[/math][5]
RzDIN, Rtm Average distance between the highest peak and lowest valley in each sampling length, ASME Y14.36M - 1996 Surface Texture Symbols [math]\displaystyle{ RzDIN = \frac{1}{s} \sum_{i=1}^s Rt_i }[/math], where [math]\displaystyle{ s }[/math] is the number of sampling lengths, and [math]\displaystyle{ Rt_i }[/math] is [math]\displaystyle{ R\text{t} }[/math] for the [math]\displaystyle{ i^\text{th} }[/math] sampling length.
RzJIS Japanese Industrial Standard for [math]\displaystyle{ Rz }[/math], based on the five highest peaks and lowest valleys over the entire sampling length. [math]\displaystyle{ R\text{zJIS} = \frac{1}{5} \sum_{i=1}^{5} Rp_i - Rv_i }[/math], where [math]\displaystyle{ Rp_i }[/math] and [math]\displaystyle{ Rv_i }[/math] are the [math]\displaystyle{ i^\text{th} }[/math] highest peak, and lowest valley respectively.

Here is a common conversion table with also roughness grade numbers:

Roughness, N Roughness values, Ra RMS (µin.) Center line avg., CLA Roughness, Rt
ISO grade numbers micrometers (µm) microinches (µin.) (µin.) (µm)
N12 50 2000 2200 2000 200
N11 25 1000 1100 1000 100
N10 12.5 500 550 500 50
N9 6.3 250 275 250 25
N8 3.2 125 137.5 125 13
N7 1.6 63 69.3 63 8
N6 0.8 32 35.2 32 4
N5 0.4 16 17.6 16 2
N4 0.2 8 8.8 8 1.2
N3 0.1 4 4.4 4 0.8
N2 0.05 2 2.2 2 0.5
N1 0.025 1 1.1 1 0.3
Slope, spacing and counting parameters

Slope parameters describe characteristics of the slope of the roughness profile. Spacing and counting parameters describe how often the profile crosses certain thresholds. These parameters are often used to describe repetitive roughness profiles, such as those produced by turning on a lathe.

Parameter Description Formula
[math]\displaystyle{ Rdq ,R\Delta q }[/math] the RMS of the profile within the sampling length [math]\displaystyle{ Rdq = \sqrt{ \frac{1}{N} \sum_{i=1}^{N} \Delta_i^2} }[/math]
[math]\displaystyle{ Rda ,R\Delta a }[/math] the average absolute slope of the profile within the sampling length [math]\displaystyle{ Rda = \frac{1}{N} \sum_{i=1}^{N} |\Delta_i| }[/math]
[math]\displaystyle{ \Delta_i\! }[/math] where delta i is calculated according to ASME B46.1 and is a 5th order Savitzky–Golay smoothing filter [math]\displaystyle{ \Delta_i = \frac{1}{60 dx} (y_{i+3} - 9y_{i+2} + 45y_{i+1} - 45y_{i-1} + 9y_{i-2} - y_{i-3}) }[/math]

Other "frequency" parameters are Sm, [math]\displaystyle{ \lambda }[/math]a and [math]\displaystyle{ \lambda }[/math]q. Sm is the mean spacing between peaks. Just as with real mountains it is important to define a "peak". For Sm the surface must have dipped below the mean surface before rising again to a new peak. The average wavelength [math]\displaystyle{ \lambda }[/math]a and the root mean square wavelength [math]\displaystyle{ \lambda }[/math]q are derived from [math]\displaystyle{ \Delta }[/math]a. When trying to understand a surface that depends on both amplitude and frequency it is not obvious which pair of metrics optimally describes the balance, so a statistical analysis of pairs of measurements can be performed (e.g.: Rz and [math]\displaystyle{ \lambda }[/math]a or Ra and Sm) to find the strongest correlation.

Common conversions:

Bearing ratio curve parameters

These parameters are based on the bearing ratio curve (also known as the Abbott-Firestone curve.) This includes the Rk family of parameters.

Sketches depicting surfaces with negative and positive skew. The roughness trace is on the left, the amplitude distribution curve is in the middle, and the bearing area curve (Abbott-Firestone curve) is on the right.
Fractal theory

The mathematician Benoît Mandelbrot has pointed out the connection between surface roughness and fractal dimension.[10] The description provided by a fractal at the microroughness level may allow the control of the material properties and the type of the occurring chip formation. But fractals cannot provide a full-scale representation of a typical machined surface affected by tool feed marks; it ignores the geometry of the cutting edge. (J. Paulo Davim, 2010, op.cit.). Fractal descriptors of surfaces have an important role to play in correlating physical surface properties with surface structure. Across multiple fields, connecting physical, electrical and mechanical behavior with conventional surface descriptors of roughness or slope has been challenging. By employing measures of surface fractality together with measures of roughness or surface shape, certain interfacial phenomena including contact mechanics, friction and electrical contact resistance, can be better interpreted with respect to surface structure.[11]

Areal roughness parameters

Areal roughness parameters are defined in the ISO 25178 series. The resulting values are Sa, Sq, Sz,... Many optical measurement instruments are able to measure the surface roughness over an area. Area measurements are also possible with contact measurement systems. Multiple, closely spaced 2D scans are taken of the target area. These are then digitally stitched together using relevant software, resulting in a 3D image and accompanying areal roughness parameters.

Practical effects

Surface structure plays a key role in governing contact mechanics,[1] that is to say the mechanical behavior exhibited at an interface between two solid objects as they approach each other and transition from conditions of non-contact to full contact. In particular, normal contact stiffness is governed predominantly by asperity structures (roughness, surface slope and fractality) and material properties.

In terms of engineering surfaces, roughness is considered to be detrimental to part performance. As a consequence, most manufacturing prints establish an upper limit on roughness, but not a lower limit. An exception is in cylinder bores where oil is retained in the surface profile and a minimum roughness is required.[12]

Surface structure is often closely related to the friction and wear properties of a surface.[2] A surface with a higher fractal dimension, large [math]\displaystyle{ Ra }[/math] value, or a positive [math]\displaystyle{ Rsk }[/math], will usually have somewhat higher friction and wear quickly. The peaks in the roughness profile are not always the points of contact. The form and waviness (i.e. both amplitude and frequency) must also be considered.

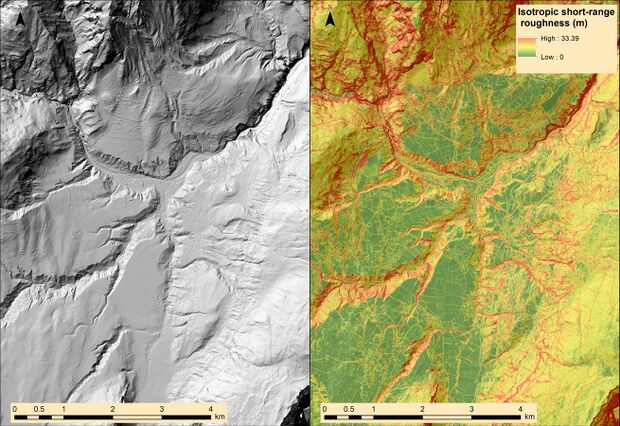
In Earth Sciences

In Earth Sciences (e.g., Shepard et al., 2001;[13] Smith, 2014[14]) and Ecology (e.g., Riley et al., 1999;[15] Sappington et al., 2007[16]) surface roughness has a quite broad meaning (e.g. Smith, 2014), with multiple definitions, and generally it is considered a multi-scale property related to surface spatial variability; it is often referred as surface texture (e.g., Trevisani et al., 2012[17]), given the evident analogies to image texture (e.g., Haralick et al. 1973;[18] Lucieer and Stein, 2005[19]) when the analysis is performed on digital elevation models. From this perspective there are various interlinks with methodologies related to geostatistics (e.g., Herzfeld and Higginson, 1996[20]), fractal analysis (e.g. Bez and Bertrand, 2011[21]) and pattern recognition (e.g., Ojala et al. 2002[22]), including many interrelations with remote sensing approaches. In the context of geomorphometry (or just morphometry, Pike, 2000[23]) the applications cover many research topics in applied and environmental geology, geomorphology, geostructural studies and soil science (e.g., Cavalli and Marchi 2008;[24] Dusséaux and Vannier, 2022;[25] Evans et al., 2022;[26] Frankel and Dolan 2007;[27] Glenn et al. 2006;[28] Grohmann et al., 2011;[29] Guth, 1999;[30] Lindsay, 2019;[31] Misiuk et al., 2021;[32] Pollyea and Fairley, 2011,[33] Trevisani and Rocca, 2015;[34] Trevisani et al. 2023;[35] Woodcock, 1977[36]).

Short-range surface roughness for an alpine area
Example of calculation of isotropic short-range surface roughness (Trevisani et al., 2023) for an alpine area. The calculation is based on a high resolution digital terrain model (2 m resolution). Many other different aspects and scales of roughness can be described.

Soil-surface roughness

Soil-surface roughness (SSR) refers to the vertical variations present in the micro- and macro-relief of a soil surface, as well as their stochastic distribution. There are four distinct classes of SSR, each one of them representing a characteristic vertical length scale; the first class includes microrelief variations from individual soil grains to aggregates on the order of 0.053–2.0 mm; the second class consists of variations due to soil clods ranging between 2 and 100 mm; the third class of soil surface roughness is systematic elevation differences due to tillage, referred to as oriented roughness (OR), ranging between 100 and 300 mm; the fourth class includes planar curvature, or macro-scale topographic features.[37]

The two first classes account for the so-called microroughness, which has been shown to be largely influenced on an event and seasonal timescale by rainfall and tillage, respectively. Microroughness is most commonly quantified by means of the Random Roughness, which is essentially the standard deviation of bed surface elevation data around the mean elevation, after correction for slope using the best-fit plane and removal of tillage effects in the individual height readings.[38] Rainfall impact can lead to either a decay or increase in microroughnesss, depending upon initial microroughness conditions and soil properties.[39] On rough soil surfaces, the action of rainsplash detachment tends to smoothen the edges of soil surface roughness, leading to an overall decrease in RR. However, a recent study which examined the response of smooth soil surfaces on rainfall showed that RR can considerably increase for low initial microroughness length scales in the order of 0 – 5 mm. It was also shown that the increase or decrease is consistent among various SSR indices.[40]

See also

References

  1. ↑ 1.0 1.1 Zhai, C.; Gan, Y.; Hanaor, D.; Proust, G.; Retraint, D. (2016). "The Role of Surface Structure in Normal Contact Stiffness". Experimental Mechanics 56 (3): 359–368. doi:10.1007/s11340-015-0107-0. https://www.researchgate.net/publication/283158084. 
  2. ↑ 2.0 2.1 Hanaor, D.; Gan, Y.; Einav, I. (2016). "Static friction at fractal interfaces". Tribology International 93: 229–238. doi:10.1016/j.triboint.2015.09.016. https://www.researchgate.net/publication/283675011. 
  3. ↑ Taufik, Mohammad; Jain, Prashant K. (2016). "A Study of Build Edge Profile for Prediction of Surface Roughness in Fused Deposition Modeling". Journal of Manufacturing Science and Engineering 138 (6). doi:10.1115/1.4032193. http://manufacturingscience.asmedigitalcollection.asme.org/article.aspx?articleid=2475087. 
  4. ↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 Whitehouse, David (2012). Surfaces and their Measurement. Boston: Butterworth-Heinemann. ISBN 978-0080972015. 
  5. ↑ 5.0 5.1 5.2 5.3 5.4 BS EN ISO 4287:2000, Geometrical product specification (GPS). Surface texture. Profile method. Terms, definitions and surface texture parameters
  6. ↑ Dietzsch M., Papenfluss K., Hartmann, T. The MOTIF method (ISO 12085: 1996)- A suitable description for functional, manufactural and metrological requirements, International Journal of Machine Tools and Manufacture, 1998, 38, No 5-6, pp. 625-632
  7. ↑ Abbott, Steven. "SPE (Surface Profile Explorer)". AbbottApps. Steven Abbott TCNF Ltd. http://www.stevenabbott.co.uk/AbbottApps/SPE/index.html. 
  8. ↑ 8.0 8.1 Degarmo, E. Paul; Black, J.; Kohser, Ronald A. (2003), Materials and Processes in Manufacturing (9th ed.), Wiley, p. 223, ISBN 0-471-65653-4. 
  9. ↑ 9.0 9.1 9.2 9.3 Surface texture : surface roughness, waviness, and lay. New York: American Society of Mechanical Engineers. 2020. ISBN 978-0-7918-7325-0. OCLC 1197629204. 
  10. ↑ Den Outer, A.; Kaashoek, J.F.; Hack, H.R.G.K. (1995). "Difficulties of using continuous fractal theory for discontinuity surfaces". International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts 32 (1): 3–9. doi:10.1016/0148-9062(94)00025-X. 
  11. ↑ Stress-Dependent Electrical Contact Resistance at Fractal Rough Surfaces Journal of Engineering Mechanics 143
  12. ↑ Carley, Larry (1 September 2000). "Engine Cylinder Bore Surface Finishes". http://www.enginebuildermag.com/2000/09/cylinder-bore-surface-finishes/. 
  13. ↑ Shepard, Michael K.; Campbell, Bruce A.; Bulmer, Mark H.; Farr, Tom G.; Gaddis, Lisa R.; Plaut, Jeffrey J. (2001-12-01). "The roughness of natural terrain: A planetary and remote sensing perspective". Journal of Geophysical Research: Planets 106 (E12): 32777–32795. doi:10.1029/2000je001429. ISSN 0148-0227. Bibcode: 2001JGR...10632777S. http://dx.doi.org/10.1029/2000je001429. 
  14. ↑ Smith, Mark W. (September 2014). "Roughness in the Earth Sciences". Earth-Science Reviews 136: 202–225. doi:10.1016/j.earscirev.2014.05.016. ISSN 0012-8252. Bibcode: 2014ESRv..136..202S. http://dx.doi.org/10.1016/j.earscirev.2014.05.016. 
  15. ↑ Riley, S.J.; DeGloria, S.D.; Elliott, R. (1999). "A terrain ruggedness index that quantifies topographic heterogeneity. Intermountain". Intermountain Journal of Science 5: 23–27. 
  16. ↑ SAPPINGTON, J. MARK; LONGSHORE, KATHLEEN M.; THOMPSON, DANIEL B. (July 2007). "Quantifying Landscape Ruggedness for Animal Habitat Analysis: A Case Study Using Bighorn Sheep in the Mojave Desert". Journal of Wildlife Management 71 (5): 1419–1426. doi:10.2193/2005-723. ISSN 0022-541X. http://dx.doi.org/10.2193/2005-723. 
  17. ↑ Trevisani, Sebastiano; Cavalli, Marco; Marchi, Lorenzo (August 2012). "Surface texture analysis of a high-resolution DTM: Interpreting an alpine basin". Geomorphology 161-162: 26–39. doi:10.1016/j.geomorph.2012.03.031. ISSN 0169-555X. Bibcode: 2012Geomo.161...26T. http://dx.doi.org/10.1016/j.geomorph.2012.03.031. 
  18. ↑ Haralick, Robert M.; Shanmugam, K.; Dinstein, Its'Hak (November 1973). "Textural Features for Image Classification". IEEE Transactions on Systems, Man, and Cybernetics SMC-3 (6): 610–621. doi:10.1109/tsmc.1973.4309314. ISSN 0018-9472. http://dx.doi.org/10.1109/tsmc.1973.4309314. 
  19. ↑ Lucieer, Arko; Stein, Alfred (March 2005). "Texture-based landform segmentation of LiDAR imagery". International Journal of Applied Earth Observation and Geoinformation 6 (3–4): 261–270. doi:10.1016/j.jag.2004.10.008. ISSN 1569-8432. Bibcode: 2005IJAEO...6..261L. http://dx.doi.org/10.1016/j.jag.2004.10.008. 
  20. ↑ Herzfeld, Ute Christina; Higginson, Chris A. (February 1996). "Automated geostatistical seafloor classification—Principles, parameters, feature vectors, and discrimination criteria". Computers & Geosciences 22 (1): 35–52. doi:10.1016/0098-3004(96)89522-7. ISSN 0098-3004. Bibcode: 1996CG.....22...35H. http://dx.doi.org/10.1016/0098-3004(96)89522-7. 
  21. ↑ Bez, Nicolas; Bertrand, Sophie (2010-06-09). "The duality of fractals: roughness and self-similarity". Theoretical Ecology 4 (3): 371–383. doi:10.1007/s12080-010-0084-y. ISSN 1874-1738. http://dx.doi.org/10.1007/s12080-010-0084-y. 
  22. ↑ Ojala, T.; Pietikainen, M.; Maenpaa, T. (July 2002). "Multiresolution gray-scale and rotation invariant texture classification with local binary patterns". IEEE Transactions on Pattern Analysis and Machine Intelligence 24 (7): 971–987. doi:10.1109/tpami.2002.1017623. ISSN 0162-8828. http://dx.doi.org/10.1109/tpami.2002.1017623. 
  23. ↑ Pike, R.J. (2000-03-01). "Geomorphometry - diversity in quantitative surface analysis". Progress in Physical Geography 24 (1): 1–20. doi:10.1191/030913300674449511. ISSN 1477-0296. http://dx.doi.org/10.1191/030913300674449511. 
  24. ↑ Cavalli, M.; Marchi, L. (2008-04-11). "Characterisation of the surface morphology of an alpine alluvial fan using airborne LiDAR". Natural Hazards and Earth System Sciences 8 (2): 323–333. doi:10.5194/nhess-8-323-2008. ISSN 1684-9981. Bibcode: 2008NHESS...8..323C. http://dx.doi.org/10.5194/nhess-8-323-2008. 
  25. ↑ Dusséaux, Richard; Vannier, Edwige (August 2022). "Soil surface roughness modelling with the bidirectional autocorrelation function". Biosystems Engineering 220: 87–102. doi:10.1016/j.biosystemseng.2022.05.012. ISSN 1537-5110. http://dx.doi.org/10.1016/j.biosystemseng.2022.05.012. 
  26. ↑ Evans, Ben R.; Möller, Iris; Spencer, Tom; Smith, Geoff (2019-05-30). "Dynamics of salt marsh margins are related to their three‐dimensional functional form". Earth Surface Processes and Landforms. doi:10.1002/esp.4614. ISSN 0197-9337. http://dx.doi.org/10.1002/esp.4614. 
  27. ↑ Frankel, Kurt L.; Dolan, James F. (2007-05-26). "Characterizing arid region alluvial fan surface roughness with airborne laser swath mapping digital topographic data" (in en). Journal of Geophysical Research 112 (F2): F02025. doi:10.1029/2006JF000644. ISSN 0148-0227. Bibcode: 2007JGRF..112.2025F. http://doi.wiley.com/10.1029/2006JF000644. 
  28. ↑ Glenn, Nancy F.; Streutker, David R.; Chadwick, D. John; Thackray, Glenn D.; Dorsch, Stephen J. (January 2006). "Analysis of LiDAR-derived topographic information for characterizing and differentiating landslide morphology and activity". Geomorphology 73 (1–2): 131–148. doi:10.1016/j.geomorph.2005.07.006. ISSN 0169-555X. Bibcode: 2006Geomo..73..131G. http://dx.doi.org/10.1016/j.geomorph.2005.07.006. 
  29. ↑ Grohmann, Carlos Henrique; Smith, Mike J.; Riccomini, Claudio (April 2011). "Multiscale Analysis of Topographic Surface Roughness in the Midland Valley, Scotland". IEEE Transactions on Geoscience and Remote Sensing 49 (4): 1200–1213. doi:10.1109/tgrs.2010.2053546. ISSN 0196-2892. Bibcode: 2011ITGRS..49.1200G. http://dx.doi.org/10.1109/tgrs.2010.2053546. 
  30. ↑ Guth, Peter L. (1999-01-29). "Quantifying topographic fabric: eigenvector analysis using digital elevation models". SPIE Proceedings (SPIE) 3584: 233. doi:10.1117/12.339825. Bibcode: 1999SPIE.3584..233G. http://dx.doi.org/10.1117/12.339825. 
  31. ↑ Lindsay, John B.; Newman, Daniel R.; Francioni, Anthony (2019-07-22). "Scale-Optimized Surface Roughness for Topographic Analysis". Geosciences 9 (7): 322. doi:10.3390/geosciences9070322. ISSN 2076-3263. Bibcode: 2019Geosc...9..322L. 
  32. ↑ Misiuk, Benjamin; Lecours, V.; Dolan, M. F. J.; Robert, K. (2021-07-04). "Evaluating the Suitability of Multi-Scale Terrain Attribute Calculation Approaches for Seabed Mapping Applications" (in en). Marine Geodesy 44 (4): 327–385. doi:10.1080/01490419.2021.1925789. ISSN 0149-0419. https://www.tandfonline.com/doi/full/10.1080/01490419.2021.1925789. 
  33. ↑ Pollyea, Ryan M.; Fairley, Jerry P. (July 2011). "Estimating surface roughness of terrestrial laser scan data using orthogonal distance regression". Geology 39 (7): 623–626. doi:10.1130/g32078.1. ISSN 1943-2682. Bibcode: 2011Geo....39..623P. http://dx.doi.org/10.1130/g32078.1. 
  34. ↑ Trevisani, S.; Rocca, M. (August 2015). "MAD: robust image texture analysis for applications in high resolution geomorphometry". Computers & Geosciences 81: 78–92. doi:10.1016/j.cageo.2015.04.003. ISSN 0098-3004. http://dx.doi.org/10.1016/j.cageo.2015.04.003. 
  35. ↑ Trevisani, S.; Teza, G.; Guth, P. (April 2023). "A simplified geostatistical approach for characterizing key aspects of short-range roughness" (in en). CATENA 223: 106927. doi:10.1016/j.catena.2023.106927. Bibcode: 2023Caten.22306927T. https://linkinghub.elsevier.com/retrieve/pii/S0341816223000188. 
  36. ↑ Woodcock, N. H. (1977). "Specification of fabric shapes using an eigenvalue method". Geological Society of America Bulletin 88 (9): 1231. doi:10.1130/0016-7606(1977)88<1231:sofsua>2.0.co;2. ISSN 0016-7606. Bibcode: 1977GSAB...88.1231W. 
  37. ↑ Römkens, M.J.M; Helming, K; Prasad, S.N (2002). "Soil erosion under different rainfall intensities, surface roughness, and soil water regimes". CATENA 46 (2–3): 103–123. doi:10.1016/s0341-8162(01)00161-8. Bibcode: 2002Caten..46..103R. 
  38. ↑ Allmaras, R. R. (1966) (in en). Total Porosity and Random Roughness of the Interrow Zone as Influenced by Tillage. Agricultural Research Service, U.S. Department of Agriculture. https://books.google.com/books?id=ipMYogEACAAJ. 
  39. ↑ Potter, K. N. (1990). "Soil Properties Effect on Random Roughness Decay by Rainfall" (in en). Transactions of the ASAE 33 (6): 1889–1892. doi:10.13031/2013.31554. 
  40. ↑ Abban, B. K. B.; Papanicolaou, A. N. (Thanos); Giannopoulos, C. P.; Dermisis, D. C.; Wacha, K. M.; Wilson, C. G.; Elhakeem, M. (2017-09-28). "Quantifying the changes of soil surface microroughness due to rainfall impact on a smooth surface". Nonlinear Processes in Geophysics 24 (3): 569–579. doi:10.5194/npg-24-569-2017. ISSN 1607-7946. Bibcode: 2017NPGeo..24..569A. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Surface_roughness&oldid=3280261"
Licensed under CC BY-SA 3.0 | Source: https://handwiki.org/wiki/Physics:Surface_roughness
36 views | Status: cached on July 19 2024 20:22:50
↧ Download this article as ZWI file
Encyclosphere.org EncycloReader is supported by the EncyclosphereKSF