Tennis racket theorem

Principal axes of a tennis racket.

Composite video of a tennis racquet rotated around the three axes – the intermediate one flips from the light edge to the dark edge (note that the numbering is off-set by 1 from the diagram above)

Title page of "Théorie Nouvelle de la Rotation des Corps", 1852 printing

The tennis racket theorem or intermediate axis theorem, is a kinetic phenomenon of classical mechanics which describes the movement of a rigid body with three distinct principal moments of inertia. It has also dubbed the Dzhanibekov effect, after Soviet cosmonaut Vladimir Dzhanibekov, who noticed one of the theorem's logical consequences whilst in space in 1985.^[1] Formally the effect had been known for at least 150 years, having been described by Louis Poinsot in 1834.^[2][3]

The theorem describes the following effect: rotation of an object around its first and third principal axes is stable, whereas rotation around its second principal axis (or intermediate axis) is not.

This can be demonstrated by the following experiment: hold a tennis racket at its handle, with its face being horizontal, and throw it in the air such that it performs a full rotation around its horizontal axis perpendicular to the handle (ê₂ in the diagram, ê₁ in the video), and then catch the handle. In almost all cases, during that rotation the face will also have completed a half rotation, so that the other face is now up. By contrast, it is easy to throw the racket so that it will rotate around the handle axis (ê₁ in the diagram) without accompanying half-rotation around another axis; it is also possible to make it rotate around the vertical axis perpendicular to the handle (ê₃ in the diagram) without any accompanying half-rotation.

The experiment can be performed with any object that has three different moments of inertia, for instance with a book, remote control, or smartphone. The effect occurs whenever the axis of rotation differs only slightly from the object's second principal axis; air resistance or gravity are not necessary.^[4]

Theory

File:Dzhanibekov effect.ogv The tennis racket theorem can be qualitatively analysed with the help of Euler's equations. Under torque–free conditions, they take the following form:

[math]\displaystyle{ \begin{align} I_1\dot{\omega}_1 &= -(I_3-I_2)\omega_3\omega_2~~~~~~~~~~~~~~~~~~~~\text{(1)}\\ I_2\dot{\omega}_2 &= -(I_1-I_3)\omega_1\omega_3~~~~~~~~~~~~~~~~~~~~\text{(2)}\\ I_3\dot{\omega}_3 &= -(I_2-I_1)\omega_2\omega_1~~~~~~~~~~~~~~~~~~~~\text{(3)} \end{align} }[/math]

Here [math]\displaystyle{ I_1, I_2, I_3 }[/math] denote the object's principal moments of inertia, and we assume [math]\displaystyle{ I_1 \lt I_2 \lt I_3 }[/math]. The angular velocities around the object's three principal axes are [math]\displaystyle{ \omega_1, \omega_2, \omega_3 }[/math] and their time derivatives are denoted by [math]\displaystyle{ \dot\omega_1, \dot\omega_2, \dot\omega_3 }[/math].

Stable rotation around the first and third principal axis

Consider the situation when the object is rotating around axis with moment of inertia [math]\displaystyle{ I_1 }[/math]. To determine the nature of equilibrium, assume small initial angular velocities along the other two axes. As a result, according to equation (1), [math]\displaystyle{ ~\dot{\omega}_1 }[/math] is very small. Therefore, the time dependence of [math]\displaystyle{ ~\omega_1 }[/math] may be neglected.

Now, differentiating equation (2) and substituting [math]\displaystyle{ \dot{\omega}_3 }[/math] from equation (3),

[math]\displaystyle{ \begin{align} I_2 \ddot{\omega}_2 &= -(I_1-I_3) \omega_1\dot{\omega}_3 \\ I_3 I_2 \ddot{\omega}_2 &= (I_1-I_3) (I_2-I_1)(\omega_1)^2\omega_2 \\ \text{i.e. }~~~~ \ddot{\omega}_2 &= \text{(negative quantity)} \cdot \omega_2 \end{align} }[/math]

because [math]\displaystyle{ I_2 - I_1 \gt 0 }[/math] and [math]\displaystyle{ I_1 - I_3 \lt 0 }[/math].

Note that [math]\displaystyle{ \omega_2 }[/math] is being opposed and so rotation around this axis is stable for the object.

Similar reasoning gives that rotation around axis with moment of inertia [math]\displaystyle{ I_3 }[/math] is also stable.

Unstable rotation around the second principal axis

Now apply the same analysis to axis with moment of inertia [math]\displaystyle{ I_2. }[/math] This time [math]\displaystyle{ \dot{\omega}_{2} }[/math] is very small. Therefore, the time dependence of [math]\displaystyle{ ~\omega_2 }[/math] may be neglected.

Now, differentiating equation (1) and substituting [math]\displaystyle{ \dot{\omega}_3 }[/math] from equation (3),

[math]\displaystyle{ \begin{align} I_1 I_3 \ddot{\omega}_1 &= (I_3 - I_2) (I_2 - I_1) (\omega_2)^2\omega_1\\ \text{i.e.}~~~~ \ddot{\omega}_1 &= \text{(positive quantity)} \cdot \omega_1 \end{align} }[/math]

Note that [math]\displaystyle{ \omega_1 }[/math] is not opposed (and therefore will grow) and so rotation around the second axis is unstable. Therefore, even a small disturbance along other axes causes the object to 'flip'.

Matrix analysis

If the object is mostly rotating along its third axis, so [math]\displaystyle{ |\omega_3 | \gg |\omega_1 |, |\omega_2 | }[/math], we can assume [math]\displaystyle{ \omega_3 }[/math] does not vary much, and write the equations of motion as a matrix equation:[math]\displaystyle{ \frac{d}{dt}\begin{bmatrix} \omega_1\\ \omega_2 \end{bmatrix} = \begin{bmatrix} 0 & -\omega_3(I_3-I_2)/I_1 \\ -\omega_3(I_1 - I_3)/I_2 & 0 \end{bmatrix} \begin{bmatrix} \omega_1\\ \omega_2 \end{bmatrix} }[/math]which has zero trace and positive determinant, implying the motion of [math]\displaystyle{ (\omega_1, \omega_2) }[/math] is a stable rotation around the origin—a neutral equilibrium point. Similarly, the point [math]\displaystyle{ (\omega_1, 0,0) }[/math] is a neutral equilibrium point, but [math]\displaystyle{ (0, \omega_2, 0) }[/math] is a saddle point.

Geometric analysis

A visualization of the instability of the intermediate axis. The magnitude of the angular momentum and the kinetic energy of a spinning object are both conserved. As a result, the angular velocity vector remains on the intersection of two ellipsoids.

During motion, both the energy and angular momentum-squared are conserved, thus we have two conserved quantities:[math]\displaystyle{ \begin{cases} 2E = \sum_i I_i \omega_i^2\\ L^2 = \sum_i I_i^2 \omega_i^2 \end{cases} }[/math]and so for any initial condition [math]\displaystyle{ \omega(0) }[/math], the trajectory of [math]\displaystyle{ \omega(t) }[/math] must stay on the intersection curve between two ellipsoids defined by [math]\displaystyle{ \begin{cases} \sum_i I_i \omega_i^2 = \sum_i I_i \omega_i(0)^2\\ \sum_i I_i^2 \omega_i^2 = \sum_i I_i^2 \omega_i(0)^2 \end{cases} }[/math]This is shown on the animation to the left.

By inspecting Euler's equations, we see that [math]\displaystyle{ \omega(t) = 0 }[/math] implies that two components of [math]\displaystyle{ \omega(t) }[/math] are zero—that is, the object is exactly spinning around one of the principal axes. In all other situations, [math]\displaystyle{ \omega(t) }[/math] must remain in motion.

By Euler's equations, if [math]\displaystyle{ \omega(t) }[/math] is a solution, then so is [math]\displaystyle{ c \omega(ct) }[/math] for any constant [math]\displaystyle{ c \gt 0 }[/math]. In particular, the motion of the body in free space (obtained by integrating [math]\displaystyle{ c\omega(ct) dt }[/math]) is exactly the same, just completed faster by a ratio of [math]\displaystyle{ c }[/math].

Consequently, we can analyze the geometry of motion with a fixed value of [math]\displaystyle{ L^2 }[/math], and vary [math]\displaystyle{ \omega(0) }[/math] on the fixed ellipsoid of constant squared angular momentum. As [math]\displaystyle{ \omega(0) }[/math] varies, the value of [math]\displaystyle{ 2E }[/math] also varies—thus giving us a varying ellipsoid of constant energy. This is shown in the animation as a fixed orange ellipsoid and increasing blue ellipsoid.

For concreteness, consider [math]\displaystyle{ I_1 = 1, I_2 = 2, I_3 = 3 }[/math], then the angular momentum ellipsoid's major axes are in ratios of [math]\displaystyle{ 1 : 1/2 : 1/3 }[/math], and the energy ellipsoid's major axes are in ratios of [math]\displaystyle{ 1 : 1/\sqrt 2 : 1/\sqrt 3 }[/math]. Thus the angular momentum ellipsoid is both flatter and sharper, as visible in the animation. In general, the angular momentum ellipsoid is always more "exaggerated" than the energy ellipsoid.

Now inscribe on a fixed ellipsoid of [math]\displaystyle{ L^2 }[/math] its intersection curves with the ellipsoid of [math]\displaystyle{ 2E }[/math], as [math]\displaystyle{ 2E }[/math] increases from zero to infinity. We can see that the curves evolve as follows:

All intersection curves of the angular momentum ellipsoid with energy ellipsoid (not shown).

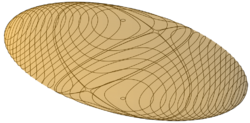
• For small energy, there is no intersection, since we need a minimum of energy to stay on the angular momentum ellipsoid.
• The energy ellipsoid first intersects the momentum ellipsoid when [math]\displaystyle{ 2E = L^2/I_3 }[/math], at the points [math]\displaystyle{ (0, 0, \pm L/I_3) }[/math]. This is when the body rotates around its axis with the largest moment of inertia.
• They intersect at two cycles around the points [math]\displaystyle{ (0, 0, \pm L/I_3) }[/math]. Since each cycle contains no point at which [math]\displaystyle{ \dot\omega=0 }[/math], the motion of [math]\displaystyle{ \omega(t) }[/math] must be a periodic motion around each cycle.
• They intersect at two "diagonal" curves that intersects at the points [math]\displaystyle{ (0, \pm L/I_2, 0) }[/math], when [math]\displaystyle{ 2E = L^2/I_2 }[/math]. If [math]\displaystyle{ \omega(t) }[/math] starts anywhere on the diagonal curves, it would approach one of the points, distance exponentially decreasing, but never actually reach the point. In other words, we have 4 heteroclinic orbits between the two saddle points.
• They intersect at two cycles around the points [math]\displaystyle{ (\pm L / I_1, 0, 0) }[/math]. Since each cycle contains no point at which [math]\displaystyle{ \dot\omega=0 }[/math], the motion of [math]\displaystyle{ \omega(t) }[/math] must be a periodic motion around each cycle.
• The energy ellipsoid last intersects the momentum ellipsoid when [math]\displaystyle{ 2E = L^2/I_1 }[/math], at the points [math]\displaystyle{ (\pm L / I_1, 0, 0) }[/math]. This is when the body rotates around its axis with the smallest moment of inertia.

The tennis racket effect occurs when [math]\displaystyle{ \omega(0) }[/math] is very close to a saddle point. The body would linger near the saddle point, then rapidly move to the other saddle point, near [math]\displaystyle{ \omega(T/2) }[/math], linger again for a long time, and so on. The motion repeats with period [math]\displaystyle{ T }[/math].

The above analysis is all done in the perspective of an observer which is rotating with the body. An observer watching the body's motion in free space would see its angular momentum vector [math]\displaystyle{ \vec L = I\vec \omega }[/math] conserved, while both its angular velocity vector [math]\displaystyle{ \vec \omega(t) }[/math] and its moment of inertia [math]\displaystyle{ I(t) }[/math] undergoing complicated motions in space. At the beginning, the observer would see both [math]\displaystyle{ \vec \omega(0), \vec L }[/math] mostly aligned with the second major axis of [math]\displaystyle{ I(0) }[/math]. After a while, the body performs a complicated motion and ends up with [math]\displaystyle{ I(T/2), \vec \omega(T/2) }[/math], and again both [math]\displaystyle{ \vec L, \vec \omega(T/2) }[/math] are mostly aligned with the second major axis of [math]\displaystyle{ I(T/2) }[/math].

Consequently, there are two possibilities: either the rigid body's second major axis is in the same direction, or it has reversed direction. If it is still in the same direction, then [math]\displaystyle{ \vec\omega(0), \vec\omega(T/2) }[/math] viewed in the rigid body's reference frame are also mostly in the same direction. However, we have just seen that [math]\displaystyle{ \omega(0) }[/math] and [math]\displaystyle{ \omega(T/2) }[/math] are near opposite saddle points [math]\displaystyle{ (0, \pm L/I_2, 0) }[/math]. Contradiction.

Qualitatively, then, this is what an observer watching in free space would observe:

• The body rotates around its second major axis for a while.
• The body rapidly undergoes a complicated motion, until its second major axis has reversed direction.
• The body rotates around its second major axis again for a while. Repeat.

This can be easily seen in the video demonstration in microgravity.

With dissipation

When the body is not exactly rigid, but can flex and bend or contain liquid that sloshes around, it can dissipate energy through its internal degrees of freedom. In this case, the body still has constant angular momentum, but its energy would decrease, until it reaches the minimal point. As analyzed geometrically above, this happens when the body's angular velocity is exactly aligned with its axis of maximal moment of inertia.

This happened to Explorer 1, the first satellite launched by the United States in 1958. The elongated body of the spacecraft had been designed to spin about its long (least-inertia) axis but refused to do so, and instead started precessing due to energy dissipation from flexible structural elements.

In general, celestial bodies large or small would converge to a constant rotation around its axis of maximal moment of inertia. Whenever a celestial body is found in a complex rotational state, it is either due to a recent impact or tidal interaction, or is a fragment of a recently disrupted progenitor.^[5]

See also

• Euler angles – Description of the orientation of a rigid body
• Physics:Moment of inertia – Scalar measure of the rotational inertia with respect to a fixed axis of rotation
• Physics:Poinsot's ellipsoid – Geometric method for visualizing a rotating rigid body
• Physics:Polhode – Curve produced by the angular velocity vector on the inertia ellipsoid

References

External links

• Dan Russell (5 March 2010). "Slow motion Dzhanibekov effect demonstration with table tennis rackets". https://www.youtube.com/watch?v=4dqCQqI-Gis. Retrieved 2 February 2017. 
• zapadlovsky (16 June 2010). "Dzhanibekov effect demonstration". https://www.youtube.com/watch?v=L2o9eBl_Gzw. Retrieved 2 February 2017.  on Mir International Space Station
• Viacheslav Mezentsev (7 September 2011). "Djanibekov effect modeled in Mathcad 14". https://www.youtube.com/watch?v=VHNvzXy-Iqs. Retrieved 2 February 2017. 
• Louis Poinsot, Théorie nouvelle de la rotation des corps, Paris, Bachelier, 1834, 170 p. OCLC 457954839 : historically, the first mathematical description of this effect.
• "Ellipsoids and The Bizarre Behaviour of Rotating Bodies". https://www.youtube.com/watch?v=l51LcwHOW7s.  - intuitive video explanation by Matt Parker

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Tennis racket theorem. Read more