Thermal conductance and resistance

Thermal resistance
Common symbols	R
SI unit	kelvin per watt (K/W)
In SI base units	kg-1⋅m-2⋅s3⋅K

Thermal conductance
Common symbols	C
SI unit	watt per kelvin (W/K)
In SI base units	kg⋅m2⋅s−3⋅K-1
Dimension	[math]\displaystyle{ \mathsf L^2 \mathsf M \mathsf T^{-3}\mathsf \Theta^{-1} }[/math]

Short description: Materials' resistance to heat transfer

In heat transfer, thermal engineering, and thermodynamics, thermal conductance and thermal resistance are fundamental concepts that describe the ability of materials or systems to conduct heat and the opposition they offer to the heat current. The ability to manipulate these properties allows engineers to control temperature gradient, prevent thermal shock, and maximize the efficiency of thermal systems. Furthermore, these principles find applications in a multitude of fields, including materials science, mechanical engineering, electronics, and energy management. Knowledge of these principles is crucial in various scientific, engineering, and everyday applications, from designing efficient temperature control, thermal insulation, and thermal management in industrial processes to optimizing the performance of electronic devices.

Thermal conductance (C) measures the ability of a material or system to conduct heat. It provides insights into the ease with which heat can pass through a particular system. It is measured in units of watts per kelvin (W/K). It is essential in the design of heat exchangers, thermally efficient materials, and various engineering systems where the controlled movement of heat is vital.

Conversely, thermal resistance (R) measures the opposition to the heat current in a material or system. It is measured in units of kelvins per watt (K/W) and indicates how much temperature difference (in kelvins) is required to transfer a unit of heat current (in watts) through the material or object. It is essential to optimize the building insulation, evaluate the efficiency of electronic devices, and enhance the performance of heat sinks in various applications.

Objects made of insulators like rubber tend to have very high resistance and low conductance, while objects made of conductors like metals tend to have very low resistance and high conductance. This relationship is quantified by resistivity or conductivity. However, the nature of a material is not the only factor as it also depends on the size and shape of an object because these properties are extensive rather than intensive. The relationship between thermal conductance and resistance is analogous to that between electrical conductance and resistance in the domain of electronics.

Thermal insulance (R-value) is a measure of a material's resistance to the heat current. It quantifies how effectively a material can resist the transfer of heat through conduction, convection, and radiation. It has the units square metre kelvins per watt (m²⋅K/W) in SI units or square foot degree Fahrenheit–hours per British thermal unit (ft²⋅°F⋅h/Btu) in imperial units. The higher the thermal insulance, the better a material insulates against heat transfer. It is commonly used in construction to assess the insulation properties of materials such as walls, roofs, and insulation products.

Practical applications

Thermal conductance and resistance have several practical applications in various fields:

Building insulation: Understanding thermal resistance helps in designing energy-efficient buildings with effective insulation materials to reduce heat transfer.
Electronics cooling: Thermal resistance is crucial for designing heat sinks and thermal management systems in electronic devices to prevent overheating. Calculating thermal conductance is crucial for designing effective heat sinks and cooling systems in electronic devices.
Automotive design: Automotive engineers use thermal resistance to optimize the cooling system and prevent overheating in engines and other vehicle components. Evaluating thermal resistance helps in designing engine components and automotive cooling systems.
Cookware design: Thermal conductance is important for designing cookware to ensure even heat distribution and cooking efficiency. Assessing thermal conductance is important in designing cookware for even heat distribution.
Heat exchangers: In industries like HVAC and chemical processing, heat exchangers use thermal conductance to efficiently transfer heat between fluids.
Aerospace: In spacecraft and aircraft, thermal resistance and conductance are critical for managing temperature variations in extreme environments. Designing spacecraft and aviation systems require considerations of thermal conductance and resistance to manage temperature extremes.
Cryogenics: Understanding thermal properties is vital for the design of cryogenic systems used in superconductors and medical applications.
Energy efficiency: In the energy sector, thermal resistance and conductance play a role in designing efficient heat exchangers for power plants and energy-efficient appliances.
Medical devices: Thermal management is crucial for medical equipment like magnetic resonance imaging (MRI) machines and laser systems to maintain precise operating temperatures. Ensuring proper thermal management is crucial for the safety and performance of medical devices and laser systems.
Food processing: The food industry uses knowledge of thermal conductance to optimize processes like pasteurization and cooking and design equipment for food processing, such as ovens and refrigeration units.
Materials science: Researchers use thermal conductance data to develop new materials for various applications, including energy storage and advanced coatings.
Environmental science: Thermal resistance is considered in climate studies to understand heat transfer in Earth's atmosphere and oceans. Evaluating thermal resistance is useful in studying soil temperature profiles for environmental and agricultural research.
Heating, ventilation, and air conditioning (HVAC): Understanding thermal resistance aids in optimizing heating, ventilation, and air conditioning systems for better energy efficiency.
Thermal packaging: Ensuring proper thermal conductance and resistance is crucial for protecting sensitive goods during transport.
Solar energy systems: Understanding thermal resistance is important in the design of solar collectors and thermal energy storage systems.
Manufacturing processes: Controlling thermal conductance is essential in processes like welding, heat treatment, and metal casting.
Geothermal energy: Assessing thermal conductance is important in geothermal heat exchangers and energy production.
Thermal imaging: Infrared cameras and thermal imaging devices use principles of thermal conductance to detect temperature variations.

Absolute thermal resistance

Absolute thermal resistance is the temperature difference across a structure when a unit of heat energy flows through it in unit time. It is the reciprocal of thermal conductance. The SI unit of absolute thermal resistance is kelvins per watt (K/W) or the equivalent degrees Celsius per watt (°C/W) – the two are the same since the intervals are equal: ΔT = 1 K = 1 °C.

The thermal resistance of materials is of great interest to electronic engineers because most electrical components generate heat and need to be cooled. Electronic components malfunction or fail if they overheat, and some parts routinely need measures taken in the design stage to prevent this.

Analogies and nomenclature

Main pages: Analogical models and Physics:Onsager reciprocal relations

Electrical engineers are familiar with Ohm's law and so often use it as an analogy when doing calculations involving thermal resistance. Mechanical and structural engineers are more familiar with Hooke's law and so often use it as an analogy when doing calculations involving thermal resistance.

type	structural analogy^[1]	hydraulic analogy	thermal	electrical analogy^[2]
quantity	impulse [math]\displaystyle{ J }[/math] [N·s]	volume [math]\displaystyle{ V }[/math] [m³]	heat [math]\displaystyle{ Q }[/math] [J]	charge [math]\displaystyle{ q }[/math] [C]
potential	displacement [math]\displaystyle{ X }[/math] [m]	pressure [math]\displaystyle{ P }[/math] [N/m²]	temperature [math]\displaystyle{ T }[/math] [K]	potential [math]\displaystyle{ V }[/math] [V = J/C]
flux	load or force [math]\displaystyle{ F }[/math] [N]	flow rate [math]\displaystyle{ Q }[/math] [m³/s]	heat transfer rate [math]\displaystyle{ \dot{Q} }[/math] [W = J/s]	current [math]\displaystyle{ I }[/math] [A = C/s]
flux density	stress [math]\displaystyle{ \sigma }[/math] [Pa = N/m²]	velocity [math]\displaystyle{ \mathbf{v} }[/math] [m/s]	heat flux [math]\displaystyle{ \mathbf{q} }[/math] [W/m²]	current density [math]\displaystyle{ \mathbf{j} }[/math] [C/(m²·s) = A/m²]
resistance	flexibility (rheology defined) [1/Pa]	fluid resistance [math]\displaystyle{ R }[/math] [...]	thermal resistance [math]\displaystyle{ R }[/math] [K/W]	electrical resistance [math]\displaystyle{ R }[/math] [Ω]
conductance	... [math]\displaystyle{ ... }[/math] [Pa]	fluid conductance [math]\displaystyle{ G }[/math] [...]	thermal conductance [math]\displaystyle{ G }[/math] [W/K]	electrical conductance [math]\displaystyle{ G }[/math] [S]
resistivity	flexibility [math]\displaystyle{ 1/k }[/math] [m/N]	fluid resistivity	thermal resistivity [(m·K)/W]	electrical resistivity [math]\displaystyle{ \rho }[/math] [Ω·m]
conductivity	stiffness [math]\displaystyle{ k }[/math] [N/m]	fluid conductivity	thermal conductivity [math]\displaystyle{ k }[/math] [W/(m·K)]	electrical conductivity [math]\displaystyle{ \sigma }[/math] [S/m]
lumped element linear model	Hooke's law [math]\displaystyle{ \Delta X = F/k }[/math]	Hagen–Poiseuille equation [math]\displaystyle{ \Delta P = Q R }[/math]	Newton's law of cooling [math]\displaystyle{ \Delta T = \dot{Q} R }[/math]	Ohm's law [math]\displaystyle{ \Delta V = IR }[/math]
distributed linear model	... [math]\displaystyle{ ... }[/math]	... [math]\displaystyle{ ... }[/math]	Fourier's law [math]\displaystyle{ \mathbf{q} = - k \boldsymbol{\nabla} T }[/math]	Ohm's law [math]\displaystyle{ \mathbf{J} = \sigma \mathbf{E} = -\sigma \boldsymbol{\nabla} V }[/math]

Explanation from an electronics point of view

Equivalent thermal circuits

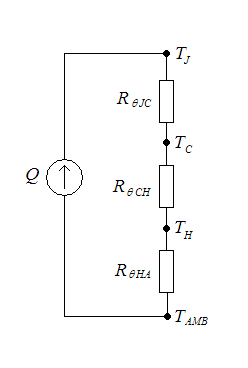
The diagram shows an equivalent thermal circuit for a semiconductor device with a heat sink:

[math]\displaystyle{ \dot{Q} }[/math] is the power dissipated by the device.
[math]\displaystyle{ T_{\rm J} }[/math] is the junction temperature in the device.
[math]\displaystyle{ T_{\rm C} }[/math] is the temperature at its case.
[math]\displaystyle{ T_{\rm H} }[/math] is the temperature where the heat sink is attached.
[math]\displaystyle{ T_{\rm amb} }[/math] is the ambient air temperature.
[math]\displaystyle{ R_{\theta \rm JC} }[/math] is the device's absolute thermal resistance from junction to case.
[math]\displaystyle{ R_{\theta \rm CH} }[/math] is the absolute thermal resistance from the case to the heatsink.
[math]\displaystyle{ R_{\theta \rm HA} }[/math] is the absolute thermal resistance of the heat sink.

The heat flow can be modelled by analogy to an electrical circuit where heat flow is represented by current, temperatures are represented by voltages, heat sources are represented by constant current sources, absolute thermal resistances are represented by resistors and thermal capacitances by capacitors.

The diagram shows an equivalent thermal circuit for a semiconductor device with a heat sink.

Example calculation

Example

Consider a component such as a silicon transistor that is bolted to the metal frame of a piece of equipment. The transistor's manufacturer will specify parameters in the datasheet called the absolute thermal resistance from junction to case (symbol: [math]\displaystyle{ R_{\theta \rm JC} }[/math]), and the maximum allowable temperature of the semiconductor junction (symbol: [math]\displaystyle{ T_{J\rm max} }[/math]). The specification for the design should include a maximum temperature at which the circuit should function correctly. Finally, the designer should consider how the heat from the transistor will escape to the environment: this might be by convection into the air, with or without the aid of a heat sink, or by conduction through the printed circuit board. For simplicity, let us assume that the designer decides to bolt the transistor to a metal surface (or heat sink) that is guaranteed to be less than [math]\displaystyle{ \Delta T_{\rm HS} }[/math] above the ambient temperature. Note: T_HS appears to be undefined.

Given all this information, the designer can construct a model of the heat flow from the semiconductor junction, where the heat is generated, to the outside world. In our example, the heat has to flow from the junction to the case of the transistor, then from the case to the metalwork. We do not need to consider where the heat goes after that, because we are told that the metalwork will conduct heat fast enough to keep the temperature less than [math]\displaystyle{ \Delta T_{\rm HS} }[/math] above ambient: this is all we need to know.

Suppose the engineer wishes to know how much power can be put into the transistor before it overheats. The calculations are as follows.

Total absolute thermal resistance from junction to ambient = [math]\displaystyle{ R_{\theta \rm JC}+R_{\theta \rm B} }[/math]

where [math]\displaystyle{ R_{\theta \rm B} }[/math] is the absolute thermal resistance of the bond between the transistor's case and the metalwork. This figure depends on the nature of the bond - for example, a thermal bonding pad or thermal transfer grease might be used to reduce the absolute thermal resistance.

Maximum temperature drop from junction to ambient = [math]\displaystyle{ T_{J\rm max} - (T_{\rm amb} + \Delta T_{\rm HS}) }[/math].

We use the general principle that the temperature drop [math]\displaystyle{ \Delta T }[/math] across a given absolute thermal resistance [math]\displaystyle{ R_{\theta} }[/math] with a given heat flow [math]\displaystyle{ \dot{Q} }[/math] through it is:

[math]\displaystyle{ \Delta T = \dot{Q} R_\theta \, }[/math].

Substituting our own symbols into this formula gives:

[math]\displaystyle{ T_{J\rm max} - (T_{\rm amb} + \Delta T_{\rm HS}) = \dot{Q}_{\rm max} (R_{\theta \rm JC} + R_{\theta \rm B} + R_{\theta \rm HA})\, }[/math],

and, rearranging,

[math]\displaystyle{ \dot{Q}_{\rm max} = { { T_{J\rm max}-(T_{\rm amb} + \Delta T_{\rm HS}) } \over { R_{\theta \rm JC} + R_{\theta \rm B}+R_{\theta \rm HA} } } }[/math]

The designer now knows [math]\displaystyle{ \dot{Q}_{\rm max} }[/math], the maximum power that the transistor can be allowed to dissipate, so they can design the circuit to limit the temperature of the transistor to a safe level.

Let us substitute some sample numbers:

[math]\displaystyle{ T_{J\rm max} = 125 \ ^{\circ}\text{C} }[/math] (typical for a silicon transistor)

[math]\displaystyle{ T_{\rm amb} = 21 \ ^{\circ}\text{C} }[/math] (a typical specification for commercial equipment)

[math]\displaystyle{ R_{\theta \rm JC} = 1.5 \ ^{\circ}\text{C}/\text{W} \, }[/math] (for a typical TO-220 package^{[citation needed]})

[math]\displaystyle{ R_{\theta \rm B} = 0.1 \ ^{\circ}\text{C}/\text{W} \, }[/math] (a typical value for an elastomer heat-transfer pad for a TO-220 package^{[citation needed]})

[math]\displaystyle{ R_{\theta \rm HA} = 4 \ ^{\circ}\text{C}/\text{W} \, }[/math] (a typical value for a heatsink for a TO-220 package^{[citation needed]})

The result is then:

[math]\displaystyle{ \dot{Q} = {{125\ ^{\circ}\text{C}-(21\ ^{\circ}\text{C})} \over {1.5\ ^{\circ}\text{C}/\text{W}+0.1\ ^{\circ}\text{C}/\text{W}+4\ ^{\circ}\text{C}/\text{W}}} = 18.6 \ \text{W} }[/math]

This means that the transistor can dissipate about 18 watts before it overheats. A cautious designer would operate the transistor at a lower power level to increase its reliability.

This method can be generalized to include any number of layers of heat-conducting materials, simply by adding together the absolute thermal resistances of the layers and the temperature drops across the layers.

Derived from Fourier's law for heat conduction

From Fourier's Law for heat conduction, the following equation can be derived, and is valid as long as all of the parameters (x and k) are constant throughout the sample.

[math]\displaystyle{ R_{\theta} = \frac{\Delta x}{A k} = \frac{\Delta x r}{A} }[/math]

where:

[math]\displaystyle{ R_{\theta} }[/math] is the absolute thermal resistance (K/W) across the thickness of the sample
[math]\displaystyle{ \Delta x }[/math] is the thickness (m) of the sample (measured on a path parallel to the heat flow)
[math]\displaystyle{ k }[/math] is the thermal conductivity (W/(K·m)) of the sample
[math]\displaystyle{ r }[/math] is the thermal resistivity (K·m/W) of the sample
[math]\displaystyle{ A }[/math] is the cross-sectional area (m²) perpendicular to the path of heat flow.

In terms of the temperature gradient across the sample and heat flux through the sample, the relationship is:

[math]\displaystyle{ R_{\theta} = \frac{\Delta x}{A \phi_q}\frac{\Delta T}{\Delta x} = \frac{\Delta T}{q} }[/math]

where:

[math]\displaystyle{ R_\theta }[/math] is the absolute thermal resistance (K/W) across the thickness of the sample,
[math]\displaystyle{ \Delta x }[/math] is the thickness (m) of the sample (measured on a path parallel to the heat flow),
[math]\displaystyle{ \phi_q }[/math] is the heat flux through the sample (W·m⁻²),
[math]\displaystyle{ \frac{\Delta T}{\Delta x} }[/math] is the temperature gradient (K·m⁻¹) across the sample,
[math]\displaystyle{ A }[/math] is the cross-sectional area (m²) perpendicular to the path of heat flow through the sample,
[math]\displaystyle{ \Delta T }[/math] is the temperature difference (K) across the sample,
[math]\displaystyle{ q }[/math] is the rate of heat flow (W) through the sample.

Problems with electrical resistance analogy

A 2008 review paper written by Philips researcher Clemens J. M. Lasance notes that: "Although there is an analogy between heat flow by conduction (Fourier's law) and the flow of an electric current (Ohm’s law), the corresponding physical properties of thermal conductivity and electrical conductivity conspire to make the behavior of heat flow quite unlike the flow of electricity in normal situations. [...] Unfortunately, although the electrical and thermal differential equations are analogous, it is erroneous to conclude that there is any practical analogy between electrical and thermal resistance. This is because a material that is considered an insulator in electrical terms is about 20 orders of magnitude less conductive than a material that is considered a conductor, while, in thermal terms, the difference between an "insulator" and a "conductor" is only about three orders of magnitude. The entire range of thermal conductivity is then equivalent to the difference in electrical conductivity of high-doped and low-doped silicon."^[3]

Measurement standards

The junction-to-air thermal resistance can vary greatly depending on the ambient conditions.^[4] (A more sophisticated way of expressing the same fact is saying that junction-to-ambient thermal resistance is not Boundary-Condition Independent (BCI).^[3]) JEDEC has a standard (number JESD51-2) for measuring the junction-to-air thermal resistance of electronics packages under natural convection and another standard (number JESD51-6) for measurement under forced convection.

A JEDEC standard for measuring the junction-to-board thermal resistance (relevant for surface-mount technology) has been published as JESD51-8.^[5]

A JEDEC standard for measuring the junction-to-case thermal resistance (JESD51-14) is relatively newcomer, having been published in late 2010; it concerns only packages having a single heat flow and an exposed cooling surface.^[6]^[7]^[8]

Resistance in composite wall

Resistances in series

When resistances are in series, the total resistance is the sum of the resistances:

[math]\displaystyle{ R_{\rm tot} = R_A + R_B + R_C + ... }[/math]

Parallel thermal resistance

Parallel thermal resistance in composite walls

Similarly to electrical circuits, the total thermal resistance for steady state conditions can be calculated as follows.

The total thermal resistance

[math]\displaystyle{ { {1 \over R_{\rm tot}} = {1 \over R_B} + {1 \over R_C} } }[/math]

(1)

Simplifying the equation, we get

[math]\displaystyle{ {R_{\rm tot} = {R_B R_C \over R_B + R_C} } }[/math]

(2)

With terms for the thermal resistance for conduction, we get

[math]\displaystyle{ {R_{t,\rm cond} = {L \over (k_b + k_c)A}} }[/math]

(3)

Resistance in series and parallel

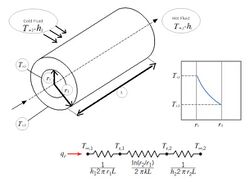
Equivalent thermal circuits for series-parallel composite wall

It is often suitable to assume one-dimensional conditions, although the heat flow is multidimensional. Now, two different circuits may be used for this case. For case (a) (shown in picture), we presume isothermal surfaces for those normal to the x- direction, whereas for case (b) we presume adiabatic surfaces parallel to the x- direction. We may obtain different results for the total resistance [math]\displaystyle{ {R_{tot} } }[/math] and the actual corresponding values of the heat transfer are bracketed by [math]\displaystyle{ {q} }[/math]. When the multidimensional effects becomes more significant, these differences are increased with increasing [math]\displaystyle{ {| k_f - k_g |} }[/math].^[9]

Radial systems

Spherical and cylindrical systems may be treated as one-dimensional, due to the temperature gradients in the radial direction. The standard method can be used for analyzing radial systems under steady state conditions, starting with the appropriate form of the heat equation, or the alternative method, starting with the appropriate form of Fourier's law. For a hollow cylinder in steady state conditions with no heat generation, the appropriate form of heat equation is ^[9]

[math]\displaystyle{ { {1 \over r}{d\over dr} \left(kr{dT \over dr} \right) = 0 } }[/math]

(4)

Where [math]\displaystyle{ {k} }[/math] is treated as a variable. Considering the appropriate form of Fourier's law, the physical significance of treating [math]\displaystyle{ {k} }[/math] as a variable becomes evident when the rate at which energy is conducted across a cylindrical surface, this is represented as

[math]\displaystyle{ { q_r = -kA {dT \over dr} = -k(2\pi rL){dT \over dr}} }[/math]

(5)

Where [math]\displaystyle{ {A = 2\pi rL} }[/math] is the area that is normal to the direction of where the heat transfer occurs. Equation 1 implies that the quantity [math]\displaystyle{ {kr(dT/dr)} }[/math] is not dependent of the radius [math]\displaystyle{ {r} }[/math], it follows from equation 5 that the heat transfer rate, [math]\displaystyle{ {q_r} }[/math] is a constant in the radial direction.

Hollow cylinder with convective surface conditions in thermal conduction

In order to determine the temperature distribution in the cylinder, equation 4 can be solved applying the appropriate boundary conditions. With the assumption that [math]\displaystyle{ {k } }[/math] is constant

[math]\displaystyle{ { T(r) = C_1\ln r + C_2 } }[/math]

(6)

Using the following boundary conditions, the constants [math]\displaystyle{ {C_1} }[/math] and [math]\displaystyle{ {C_2} }[/math] can be computed

[math]\displaystyle{ { T(r_1) = T_{s,1} } }[/math] and [math]\displaystyle{ { T(r_2) = T_{s,2} } }[/math]

The general solution gives us

[math]\displaystyle{ { T_{s,1} = C_1 \ln r_1 + C_2 } }[/math] and [math]\displaystyle{ { T_{s,2} = C_1 \ln r_2 + C_2 } }[/math]

Solving for [math]\displaystyle{ {C_1} }[/math] and [math]\displaystyle{ {C_2} }[/math] and substituting into the general solution, we obtain

[math]\displaystyle{ { T(r) = {T_{s,1} - T_{s,2} \over {\ln(r_1/r_2) } } \ln \left( {r \over r_2} \right) + T_{s,2} } }[/math]

(7)

The logarithmic distribution of the temperature is sketched in the inset of the thumbnail figure. Assuming that the temperature distribution, equation 7, is used with Fourier's law in equation 5, the heat transfer rate can be expressed in the following form

[math]\displaystyle{ {\dot{Q}_r = {2\pi Lk (T_{s,1} - T_{s,2}) \over \ln(r_2/r_1)} } }[/math]

Finally, for radial conduction in a cylindrical wall, the thermal resistance is of the form

[math]\displaystyle{ { R_{t,\mathrm{cond}} = {\ln(r_2/r_1) \over 2\pi Lk} } }[/math] such that [math]\displaystyle{ {r_2 \gt r_1} }[/math]

References

↑ Tony Abbey. "Using FEA for Thermal Analysis". Desktop Engineering magazine. 2014 June. p. 32.
↑ "The Design of Heatsinks".
↑ ^3.0 ^3.1 Lasance, C. J. M. (2008). "Ten Years of Boundary-Condition- Independent Compact Thermal Modeling of Electronic Parts: A Review". Heat Transfer Engineering 29 (2): 149–168. doi:10.1080/01457630701673188. Bibcode: 2008HTrEn..29..149L.
↑ Ho-Ming Tong; Yi-Shao Lai; C.P. Wong (2013). Advanced Flip Chip Packaging. Springer Science & Business Media. pp. 460–461. ISBN 978-1-4419-5768-9. https://archive.org/details/advancedflipchip00lanz.
↑ Younes Shabany (2011). Heat Transfer: Thermal Management of Electronics. CRC Press. pp. 111–113. ISBN 978-1-4398-1468-0.
↑ Clemens J.M. Lasance; András Poppe (2013). Thermal Management for LED Applications. Springer Science & Business Media. p. 247. ISBN 978-1-4614-5091-7.
↑ "Experiment vs. Simulation, Part 3: JESD51-14". 2013-02-22. http://www.electronics-cooling.com/2013/02/experiment-vs-simulation-part-3-jesd51-14/.
↑ Schweitzer, D.; Pape, H.; Chen, L.; Kutscherauer, R.; Walder, M. (2011). "2011 27th Annual IEEE Semiconductor Thermal Measurement and Management Symposium". pp. 222. doi:10.1109/STHERM.2011.5767204. ISBN 978-1-61284-740-5.
↑ ^9.0 ^9.1 Incropera, Dewitt, Bergman, Lavine, Frank P., David P., Theodore L., Adrienne S. (2013). Principles of Heat and Mass Transfer. John Wiley & Sons; 7th Edition, Interna edition. ISBN 978-0470646151.

10. K Einalipour, S. Sadeghzadeh, F. Molaei. “Interfacial thermal resistance engineering for polyaniline (C3N)-graphene heterostructure”, The Journal of Physical Chemistry, 2020. DOI:10.1021/acs.jpcc.0c02051

Michael Lenz, Günther Striedl, Ulrich Fröhler (January 2000) Thermal Resistance, Theory and Practice. Infineon Technologies AG, Munich, Germany .
Directed Energy, Inc./IXYSRF (March 31, 2003) R Theta And Power Dissipation Technical Note. Ixys RF, Fort Collins, Colorado. Example thermal resistance and power dissipation calculation in semiconductors.

External links

Guoping Xu (2006), Thermal Management for Electronic Packaging, Sun Microsystems
Update on JEDEC Thermal Standards
The importance of Soil Thermal Resistivity for power companies

0.00

(0 votes)

Original source: https://en.wikipedia.org/wiki/Thermal conductance and resistance. Read more

[1] Tony Abbey. "Using FEA for Thermal Analysis". Desktop Engineering magazine. 2014 June. p. 32.

[2] "The Design of Heatsinks".

[Lasance-3] 3.0 ^3.1 Lasance, C. J. M. (2008). "Ten Years of Boundary-Condition- Independent Compact Thermal Modeling of Electronic Parts: A Review". Heat Transfer Engineering 29 (2): 149–168. doi:10.1080/01457630701673188. Bibcode: 2008HTrEn..29..149L.

[TongLai2013-4] Ho-Ming Tong; Yi-Shao Lai; C.P. Wong (2013). Advanced Flip Chip Packaging. Springer Science & Business Media. pp. 460–461. ISBN 978-1-4419-5768-9. https://archive.org/details/advancedflipchip00lanz.

[Shabany2011-5] Younes Shabany (2011). Heat Transfer: Thermal Management of Electronics. CRC Press. pp. 111–113. ISBN 978-1-4398-1468-0.

[LasancePoppe2013-6] Clemens J.M. Lasance; András Poppe (2013). Thermal Management for LED Applications. Springer Science & Business Media. p. 247. ISBN 978-1-4614-5091-7.

[7] "Experiment vs. Simulation, Part 3: JESD51-14". 2013-02-22. http://www.electronics-cooling.com/2013/02/experiment-vs-simulation-part-3-jesd51-14/.

[8] Schweitzer, D.; Pape, H.; Chen, L.; Kutscherauer, R.; Walder, M. (2011). "2011 27th Annual IEEE Semiconductor Thermal Measurement and Management Symposium". pp. 222. doi:10.1109/STHERM.2011.5767204. ISBN 978-1-61284-740-5.

[Incropera,_Dewitt,_Bergman,_Lavine_2013-9] 9.0 ^9.1 Incropera, Dewitt, Bergman, Lavine, Frank P., David P., Theodore L., Adrienne S. (2013). Principles of Heat and Mass Transfer. John Wiley & Sons; 7th Edition, Interna edition. ISBN 978-0470646151.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]