Timeline of fluid and continuum mechanics

This timeline describes the major developments, both experimental and theoretical understanding of fluid mechanics and continuum mechanics. This timeline includes developments in:

• Theoretical models of hydrostatics, hydrodynamics and aerodynamics.
• Hydraulics
• Elasticity
• Mechanical waves and acoustics
• Valves and fluidics
• Gas laws
• Turbulence modeling
• Plasticity and rheology
• Quantum fluids like Bose–Einstein condensates and superfluidity
• Microfluidics

• Before 3000 BC – Civilization starts by settling around rivers, coast and lakes.
• 3000 BC – Irrigation techniques develop in Mesopotamia and Ancient Egypt.^[1] Indus Valley Civilisation develops city-wide drainage systems and toilet systems.^[1] Egyptians develop reed boats.
• 2300 BC – Construction of the Nahrawan Canal.^[1]
• 2000–1500 BC – First dams constructed in India to control water.^[1]
• 1700 BC – Windmill are used in Babylonia to pump water.
• 14th century BC – Water clock are developed in Egypt under the reign of Amenhotep III. Clepsydra water clock design is developed in ancient Greece.^[1]
• 6th century BC – Theodorus of Samos invents the water level. Ancient Rome's drainage system is designed during the reign of Tarquinius Priscus. Rome's Cloaca Maxima is constructed by lining a river bed with stone. Tunnel of Eupalinos is constructed in Samos.^[1]
• 4th century BC – Mencius describes how to measure an elephant using displacement of water. Development of rain gauges in India.^[1] Aqua Appia first Roman aqueduct is built in Rome.^[1]
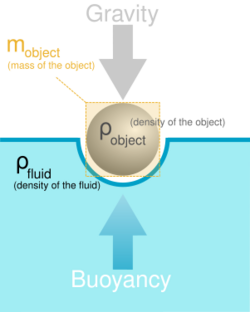
• 3rd century BC – Archimedes published On Floating Bodies describing the general principle for buoyancy and hydrostatics. Archimedes develops Archimedes' screw for water extraction.^[1]
• 2nd century BC – The aqueduct Aqua Tepula and Aqua Marcia aqueducts are completed in Rome.^[1] Zhang Heng of Han dynasty designs the first known seismoscope.^[2][3][4]
• 1st century BC – Frontinus publishes his treatise De aquaeductu on Roman water engineering. Hero of Alexandria makes a series of experiments and devices with fluids, including the aeolipile steam device and wind harnessing devices.

• 8th–13th century – Arab Agricultural Revolution
• 725 – Northumbrian monk Bede publishes The Reckoning of Time, which includes a quantitative description of the influence of the moon and the sun over the tides.
• c. 850– Abu Ma'shar al-Balkhi (Albumasar) publishes his Kitab al-madkhal al-kabir recording the Moon position and tides, he recognizes that there are two tides in day.^[5]
• 850 – The Book of Ingenious Devices is published by the Banū Mūsā brothers, describing a number of early automatic controls using fluid mechanics.^[6][7]
• 1206 – Ismail al-Jazari invented water-powered programmable automata/robots and water music devices.^[8]

• 1432 – Portuguese develop caravels for long-distance ocean travel.^[1]
• 1450 –Nicholas of Cusa publishes his experiments with fluids in Idiota de staticis experimentis, including the first proposal to measure air moisture using wool.
• 1480-1510 – Leonardo da Vinci develops the first sophisticated parachute, the first descriptions of capillary action, and the first turbine water wheels designs.^[1]
• 1586 – Simon Stevin publishes De Beghinselen des Waterwichts ("Principles on the weight of water") on hydrostatics. He first details the hydrostatic paradox.^[9]
• 1596 – Galileo Galilei produces the first (Galileo) thermometer.^[1]

• 1619 – Benedetto Castelli published Della Misura dell'Acque Correnti ("On the Measurement of Running Waters"), one of the foundations of modern hydrodynamics.^[10]
• 1619 – William Harvey provides first model of the human circulatory system.^[1]
• 1624 – Jan Baptist van Helmont coins the term "gas".^[1]
• 1631 – René Descartes first describes the principle of the mercury barometer.
• 1643 – Evangelista Torricelli provides a relation between the speed of fluid flowing from an orifice to the height of fluid above the opening, given by Torricelli's law. He also builds a mercury barometer and does a series of experiments on vacuum.^[1]
• 1650 – Otto von Guericke invents the first vacuum pump.^[1]
• 1653–1663 Blaise Pascal establishes Pascal's law of hydrostatics.
• 1662-1678 – Robert Boyle and Edme Mariotte independently discover a gas law that describes the relationship between pressure and volume given by Boyle's law (or Boyle-Mariotte's law).
• 1678 – Robert Hooke publishes Hooke's law describing linear deformation of a spring.
• 1687 – Isaac Newton publishes Philosophiæ Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy), introducing the Newton's laws of motion of classical mechanics.^[11] He also introduces the concept of Newtonian fluid.

• 1713 – Antoine Parent introduces the concept of shear stress.^[12]
• 1714 – Daniel Gabriel Fahrenheit develops the mercury-in-glass thermometer along the Fahrenheit temperature scale.^[1]
• 1718–1719 – James Jurin writes the law of capillary action, known as Jurin's law.
• 1727 – Leonhard Euler introduces linear elasticity and the Young's modulus.^[12]
• 1732 – Henri Pitot discovers how to measure the pressure from the speed of a fluid using a Pitot tube.^[13]
• 1738 – Daniel Bernoulli publishes Hydrodynamica discussing the mathematical relation between pressure and velocity of fluids according to Bernoulli's principle.^[1]
• 1742 – Anders Celsius designs a thermometer with the Celsius scale.
• 1744 – Euler introduces the concept of deformation and strain.^[12]
• 1747 – Jean le Rond d'Alembert's formula for the solutions of the wave equation in a string gets published.^[14]
• 1752 – D'Alembert show an inconsistency of treating fluids as inviscid incompressible fluids, known as d'Alembert's paradox.
• 1757 – Euler introduces the Euler equations of fluid dynamics for incompressible and non-viscous flow. He also introduces the mathematical model for buckling.^[12]
• 1764 – James Watt develops his steam water condenser leading to efficient steam engines.^[1]
• 1765 – Jean-Charles de Borda experiments with whirling arm experiments. He corrects the available theories of air friction.^[15]
• 1766 – de Borda publishes "Mémoire sur l'Écoulement des Fluides par les Orifices des Vases" on hydraulics and resistance of fluid through orifices. He comes up with Borda–Carnot equation.
• 1768 – Antoine de Chézy provides a semi-empirical formula for resistance of open channel flow, described by Chézy formula.^[1]
• 1775 – Pierre-Simon Girard invents the water turbine.^[1]
• 1776 – Charles Bossut, supervised by the Marquis de Condorcet and d'Alembert, publishes Nouvelles expériences sur la resistance de fluides, a report on a series experiments to test currents theories of hydraulics.
• 1775-76 – Pierre-Simon Laplace introduces the mathematical theory for tidal forces on oceans.^[16]
• 1779 – Pierre-Louis-Georges du Buat publishes Principes de l'hydraulique ("Principles of hydraulics"), with semiempirical equations for the flow of water through pipes and open channels.^[17][18]
• 1780 – Jacques Charles discover a gas law that describes the relationship between temperature and volume, given by Charles's law.
• 1782 – The Montgolfier brothers invent the hot air balloon.^[1]
• 1785 – First theories of friction are introduced by Charles-Augustin de Coulomb.^[19]
• 1787 – Ernst Chladni, publishes his experiments on vibrational modes of thin solid surfaces, describing the Chladni patterns created using a violin bow, based on previous experiments by Hooke.
• 1797 – Giovanni Battista Venturi discovers the Venturi effect.^[20]
• 1799 – George Cayley introduces modern fixed wing-machines and identifies three important factors for flying machines: thrust, lift, drag, and weight.

• 1801 – Robert Fulton develops the first submarine.^[1]
• 1805-1806 – The development of Young–Laplace equation by Thomas Young and improved by Laplace.^[21]
• 1808-1809 – Joseph Louis Gay-Lussac describes the law of combining gases.
• 1811–1812 – Amedeo Avogadro and André-Marie Ampère independently discover a gas law relating volume and quantity of gas, given by Avogadro's law (or Avogadro-Ampère's law).
• 1821 – Claude-Louis Navier introduces viscosity in to Euler equations of fluids.
• 1821 – Sophie Germain wins a contest of the French Academy of Sciences for providing a partial theory for the vibration of an elastic surfaces.^[22]
• 1827 – Augustin-Louis Cauchy introduces the Cauchy stress tensor and the concept of stress in elasticity.^[23][12]
• 1827 – Robert Brown (botanist, born 1773), identifies the Brownian motion of pollen grains suspended in water.
• 1831– Michael Faraday first describes vibrational modes in liquids, known as Faraday waves.^[24][25]
• 1831-1833– Thomas Graham first studies the diffusion in gases.^[26]
• 1834 – Benoît Paul Émile Clapeyron unifies many of the empirical gas laws into the ideal gas law.
• 1834 – John Scott Russell first describes the observation of solitary waves.
• 1837 – George Green find the minimal number of elastic moduli.^[12]
• 1838-40 – Gotthilf Hagen and Jean Léonard Marie Poiseuille study laminar flow, independently establishing Hagen–Poiseuille equation.^[1]
• 1841 – George Biddell Airy publishes the first correct formulation of Airy wave theory of water waves.^[27]
• 1842 – Christian Doppler introduces the Doppler effect.
• 1842 – James Prescott Joule discovers magnetostriction, the first magnetomechanical effect.^[28]
• 1842-1850 – Stokes completes the equations of motions of fluids, now referred as Navier–Stokes equations. He also extends Airy wave theory to non-linear Stokes wave theory.^[29]
• 1852 – Heinrich Gustav Magnus describes the Magnus effect.^[30][31]
• 1855 – Lord Kelvin calculates the thermodynamics work and energy due to elastic deformation.^[12]
• 1855 – Adolf Eugen Fick publishes Fick's laws of diffusion.
• 1857 – Henry Darcy studies flow through porous media, leading to the discovery of Darcy's law.^[32]
• 1857 – Rudolf Clausius introduces the first model for the kinetic theory of gases.^[33]
• 1859 – W. H. Besant introduces an equation for the dynamics of bubbles in an incompressible fluid.^[34]
• 1860 – James Clerk Maxwell introduces the Maxwell distribution of velocity of classical gas molecules.
• 1863 –Hermann von Helmholtz publishes Sensations of Tone on the physics of sound perception.
• 1864 – August Toepler invents Schlieren photography.
• 1865 – Lord Kelvin introduces the Kelvin material model for viscoelasticity.^[35]
• 1856 – Carlo Marangoni studies the tears of wine, now explained by the Marangoni effect.
• 1867 – Helmholtz works on Helmholtz's theorems for vortex dynamics.
• 1867 – James Clerk Maxwell introduces the Maxwell material model for viscoelasticity.
• 1868–1871 – Helmholtz and Kelvin study and develop the theory of the Kelvin–Helmholtz instability.^[36]
• 1870 – William Rankine develops an equation for the study of shock waves.
• 1871 – Francis Herbert Wenham designs and builds the first wind tunnel.^[37][38]
• 1872-1877 – Joseph Valentin Boussinesq introduces the concept of turbulence in forms of eddy viscosity, as well as Boussinesq approximation for water waves and Boussinesq approximation for buoyancy.^[1]
• 1873 – Johannes Diderik van der Waals introduces the Van der Waals equation.^[39]
• 1883 – Osborne Reynolds demonstrates the transition and differences between laminar and turbulent pipe flow.^[1]
• 1885 – Lord Rayleigh predicts the existence of Rayleigh surface waves.^[40]
• 1885 – Helmholtz describes the concept of Helmholtz resonance.^[41]
• 1887 – Pierre Henri Hugoniot based on the work of Rankine, introduces the Rankine–Hugoniot conditions to model shock waves.
• 1887 – First models of supersonic waves by Ernst Mach.^[42] He introduces the concept of Mach number.
• 1888 – First commercial Venturi tube by Clemens Herschel.^[43]
• 1888-1890 – Independently, Henry R. A. Mallock and Maurice Couette find the mathematical solution for the Couette flow.^[44]
• 1889 – Robert Manning produces Manning's formula for open channel flow.^[1]
• 1893 – Carl Barus develops the theory of the die swell in complex fluids.
• 1895 – Diederik Korteweg and Gustav de Vries (1895) rediscover the Korteweg–De Vries equation first treated by Boussinesq and introduce the idea of soliton solutions.^[45][46]

• 1902 – Martin Kutta discusses the air flow through an airfoil using the Kutta condition.
• 1903 – The Wright brothers carry the first successful manned airplane flight.^[1]
• 1903 – Walther Ritz introduces the Ritz method to study beam theory and Chladni figures.^[47]
• 1905 – First theory of dislocations by Vito Volterra.
• 1905-1906 – First successful theories of Brownian motion by Albert Einstein and Marian Smoluchowski, supporting the atomic theory of matter.
• 1906 – Richard Dixon Oldham identifies the separate arrival of p-waves, s-waves and surface waves on seismograms and found the first clear evidence that the Earth has a central core.^[48]
• 1908 – Paul Richard Heinrich Blasius introduces the concept of boundary layer.^[1]
• 1908 – Experimental confirmation of the theories of Brownian motion by Jean Baptiste Perrin.
• 1910:
  • Harry Fielding Reid put forward the elastic rebound theory for earthquakes.^[49]
  • Lord Rayleigh introduces the concept of Rayleigh flow.^[50]
  • Nikolay Zhukovsky introduces the Joukowsky transform and the Kutta–Joukowski theorem based on the work of Kutta.
  • Carl Wilhelm Oseen solves the Stokes' paradox by introducing Oseen's approximation.^[51]
• 1911 – Augustus Edward Hough Love predicts the existence of Love surface waves.^[52]
• 1915–1916 – Frederick W. Lanchester comes up with the Lanchester's laws, a set of differential equations that were practical for flying combat.
• 1915-1917 – George Barker Jeffery^[53] and Georg Hamel^[54] introduce the equations of Jeffery–Hamel flow.
• 1916 – Horace Lamb coins the term "vorticity".^[55]
• 1916 – Eugene C. Bingham studies Bingham plastics
• 1916-1923 – Lord Rayleigh, and later G. I. Taylor describe Rayleigh–Taylor instability.
• 1917 – Lamb introduces Lamb waves, generalizing Rayleigh's wave theory for thin metal plates.
• 1918 – Ludwig Prandtl develops theory of flow over airplane wings.^[1]
• 1919 – Jacob Bjerknes established the bases the Norwegian cyclone model.^[1]
• 1920 – Nikola Tesla patents the Tesla valve, opening the field of fluidics.^[56]
• 1920 – Bingham coins the term rheology from a suggestion by a colleague, Markus Reiner.^[57]
• 1921 – Theodore von Kármán introduces the turbulence model of Von Kármán swirling flow, and phenomena like Kármán vortex street.^[58]
• 1921 – Alan Arnold Griffith develops his theory of fracture mechanics.^[59]
• 1922 – Supersonic wind tunnel is invented in National Physical Laboratory (United Kingdom).
• 1926 – Einstein solves the tea leaf paradox.
• 1925 – Jakob Ackeret publishes the theory of supersonic airfoils.
• 1926 – Erwin Madelung relates quantum mechanics with hydrodynamics through his quantum hydrodynamics equations, known as Madelung equations.
• 1931 – Sylvia Skan and Victor Montague Falkner introduce the equations for the Falkner–Skan boundary layer.^[60]
• 1932 – The concept of quantum of sound (phonons) is introduced by Igor Tamm.
• 1937 – Superfluidity is discovered in helium-4 by Pyotr Kapitsa^[61] and independently by John F. Allen and Don Misener.^[62]
• 1938 – Philip Saffman and G. I. Taylor publish on Saffman–Taylor instability.^[63]
• 1937 – Lev Landau introduces Landau theory of phase transitions.
• 1940-1941 – László Tisza and Landau introduce the two-fluid model for helium.
• 1941 – Landau introduces the concept of second sound in condensed matter.^[64]
• 1942 – First magnetohydrodynamics descriptions of plasma by Hannes Alfvén. He also introduced the idea of Alfvén waves.^[65][66]
• 1948 – Milton S. Plesset improves on Rayleigh and Bessant equations for the dynamics of bubbles by including surface tension according to Rayleigh–Plesset equation.^[67]
• 1941 – Andrey Kolmogorov introduces his detailed theory of turbulence.
• 1947– Karl Weissenberg introduces the Weissenberg effect in non-Newtonian fluids.
• 1950 – James G. Oldroyd introduces the Oldroyd-B model of viscoelasticity.^[68]
• 1944 – Lewis Ferry Moody plots Darcy–Weisbach friction factor against Reynolds number for various values of relative roughness, leading to the first Moody chart.^[1]
• 1961 – Eugene P. Gross^[69] and Lev Pitaevskii^[70] introduce Gross–Pitaevskii equation for the condensation of bosons.
• 1963 – Alex Kaye describes the Kaye effect in viscoelastic liquids.
• 1972 – David Lee, Douglas Osheroff and Robert Coleman Richardson discovered two phase transitions of helium-3 along the melting curve, which were soon realized to be the two superfluid phases.
• 1990 – first micro total analysis system (μTAS) for microfluidics by Andreas Manz (fr).^[71]
• 1995 – The first Bose–Einstein condensate is produced by Eric Cornell and Carl Wieman at the University of Colorado at Boulder NIST–JILA lab, in a gas of rubidium atoms cooled to 170 nanokelvins (nK).^[72] Shortly thereafter, Wolfgang Ketterle at MIT produced a Bose–Einstein condensate in a gas of sodium atoms.

• c. 2000 – Development of droplet-based microfluidics.^[73][74]
• 2003 – Deborah S. Jin and her collaboration produce the first fermionic condensate.^[75]

• History of aviation

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Timeline of fluid and continuum mechanics. Read more