Topological quantum field theory

In gauge theory and mathematical physics, a topological quantum field theory (or topological field theory or TQFT) is a quantum field theory which computes topological invariants.

Although TQFTs were invented by physicists, they are also of mathematical interest, being related to, among other things, knot theory and the theory of four-manifolds in algebraic topology, and to the theory of moduli spaces in algebraic geometry. Donaldson, Jones, Witten, and Kontsevich have all won Fields Medals for mathematical work related to topological field theory.

In condensed matter physics, topological quantum field theories are the low-energy effective theories of topologically ordered states, such as fractional quantum Hall states, string-net condensed states, and other strongly correlated quantum liquid states.

Overview

In a topological field theory, correlation functions do not depend on the metric of spacetime. This means that the theory is not sensitive to changes in the shape of spacetime; if spacetime warps or contracts, the correlation functions do not change. Consequently, they are topological invariants.

Topological field theories are not very interesting on flat Minkowski spacetime used in particle physics. Minkowski space can be contracted to a point, so a TQFT applied to Minkowski space results in trivial topological invariants. Consequently, TQFTs are usually applied to curved spacetimes, such as, for example, Riemann surfaces. Most of the known topological field theories are defined on spacetimes of dimension less than five. It seems that a few higher-dimensional theories exist, but they are not very well understood ^{[citation needed]}.

Quantum gravity is believed to be background-independent (in some suitable sense), and TQFTs provide examples of background independent quantum field theories. This has prompted ongoing theoretical investigations into this class of models.

(Caveat: It is often said that TQFTs have only finitely many degrees of freedom. This is not a fundamental property. It happens to be true in most of the examples that physicists and mathematicians study, but it is not necessary. A topological sigma model targets infinite-dimensional projective space, and if such a thing could be defined it would have countably infinitely many degrees of freedom.)

Specific models

The known topological field theories fall into two general classes: Schwarz-type TQFTs and Witten-type TQFTs. Witten TQFTs are also sometimes referred to as cohomological field theories. See (Schwarz 2000).

Schwarz-type TQFTs

In Schwarz-type TQFTs, the correlation functions or partition functions of the system are computed by the path integral of metric-independent action functionals. For instance, in the BF model, the spacetime is a two-dimensional manifold M, the observables are constructed from a two-form F, an auxiliary scalar B, and their derivatives. The action (which determines the path integral) is

[math]\displaystyle{ S=\int\limits_M B F }[/math]

The spacetime metric does not appear anywhere in the theory, so the theory is explicitly topologically invariant. The first example appeared in 1977 and is due to A. Schwarz; its action functional is:

[math]\displaystyle{ S=\int\limits_M A\wedge dA. }[/math]

Another more famous example is Chern–Simons theory, which can be applied to knot invariants. In general, partition functions depend on a metric but the above examples are metric-independent.

Witten-type TQFTs

The first example of Witten-type TQFTs appeared in Witten's paper in 1988 (Witten 1988a), i.e. topological Yang–Mills theory in four dimensions. Though its action functional contains the spacetime metric g_αβ, after a topological twist it turns out to be metric independent. The independence of the stress-energy tensor T^αβ of the system from the metric depends on whether the BRST-operator is closed. Following Witten's example many other examples can be found in string theory.

Witten-type TQFTs arise if the following conditions are satisfied:

1. The action [math]\displaystyle{ S }[/math] of the TQFT has a symmetry, i.e. if [math]\displaystyle{ \delta }[/math] denotes a symmetry transformation (e.g. a Lie derivative) then [math]\displaystyle{ \delta S = 0 }[/math] holds.
2. The symmetry transformation is exact, i.e. [math]\displaystyle{ \delta^2 = 0 }[/math]
3. There are existing observables [math]\displaystyle{ O_1, \dots, O_n }[/math] which satisfy [math]\displaystyle{ \delta O_i = 0 }[/math] for all [math]\displaystyle{ i \in \{ 1, \dots, n\} }[/math].
4. The stress-energy-tensor (or similar physical quantities) is of the form [math]\displaystyle{ T^{\alpha \beta} = \delta G^{\alpha \beta} }[/math] for an arbitrary tensor [math]\displaystyle{ G^{\alpha \beta} }[/math].

As an example (Linker 2015): Given a 2-form field [math]\displaystyle{ B }[/math] with the differential operator [math]\displaystyle{ \delta }[/math] which satisfies [math]\displaystyle{ \delta^2=0 }[/math], then the action [math]\displaystyle{ S = \int\limits_M B \wedge \delta B }[/math] has a symmetry if [math]\displaystyle{ \delta B \wedge \delta B = 0 }[/math] since

[math]\displaystyle{ \delta S = \int\limits_M \delta(B \wedge \delta B) = \int\limits_M \delta B \wedge \delta B + \int\limits_M B \wedge \delta^2 B = 0 }[/math].

Further, the following holds (under the condition that [math]\displaystyle{ \delta }[/math] is independent on [math]\displaystyle{ B }[/math] and acts similarly to a functional derivative):

[math]\displaystyle{ \frac{\delta}{\delta B^{\alpha \beta}}S = \int\limits_M \frac{\delta}{\delta B^{\alpha \beta}}B \wedge \delta B + \int\limits_M B \wedge \delta \frac{\delta}{\delta B^{\alpha \beta}}B = \int\limits_M \frac{\delta}{\delta B^{\alpha \beta}}B \wedge \delta B - \int\limits_M \delta B \wedge \frac{\delta}{\delta B^{\alpha \beta}}B = -2 \int\limits_M \delta B \wedge \frac{\delta}{\delta B^{\alpha \beta}}B }[/math].

The expression [math]\displaystyle{ \frac{\delta}{\delta B^{\alpha \beta}}S }[/math] is proportional to [math]\displaystyle{ \delta G }[/math] with another 2-form [math]\displaystyle{ G }[/math] .

Now any averages of observables [math]\displaystyle{ \left\langle O_i \right\rangle := \int d \mu O_i e^{iS} }[/math] for the corresponding Haar measure [math]\displaystyle{ \mu }[/math] are independent on the "geometric" field [math]\displaystyle{ B }[/math] and are therefore topological:

[math]\displaystyle{ \frac{\delta}{\delta B} \left\langle O_i \right\rangle = \int d \mu O_i i \frac{\delta}{\delta B}S e^{iS} \propto \int d \mu O_i \delta G e^{iS} = \delta \left(\int d \mu O_i G e^{iS}\right) = 0 }[/math].

The third equality uses the fact that [math]\displaystyle{ \delta O_i = \delta S = 0 }[/math] and the invariance of the Haar measure under symmetry transformations. Since [math]\displaystyle{ \int d \mu O_i G e^{iS} }[/math] is only a number, its Lie derivative vanishes.

Mathematical formulations

The original Atiyah–Segal axioms

Atiyah suggested a set of axioms for topological quantum field theory, inspired by Segal's proposed axioms for conformal field theory (subsequently, Segal's idea was summarized in (Segal 2001)), and Witten's geometric meaning of supersymmetry in (Witten 1982). Atiyah's axioms are constructed by gluing the boundary with a differentiable (topological or continuous) transformation, while Segal's axioms are for conformal transformations. These axioms have been relatively useful for mathematical treatments of Schwarz-type QFTs, although it isn't clear that they capture the whole structure of Witten-type QFTs. The basic idea is that a TQFT is a functor from a certain category of cobordisms to the category of vector spaces.

There are in fact two different sets of axioms which could reasonably be called the Atiyah axioms. These axioms differ basically in whether or not they apply to a TQFT defined on a single fixed n-dimensional Riemannian / Lorentzian spacetime M or a TQFT defined on all n-dimensional spacetimes at once.

Let Λ be a commutative ring with 1 (for almost all real-world purposes we will have Λ = Z, R or C). Atiyah originally proposed the axioms of a topological quantum field theory (TQFT) in dimension d defined over a ground ring Λ as following:

• A finitely generated Λ-module Z(Σ) associated to each oriented closed smooth d-dimensional manifold Σ (corresponding to the homotopy axiom),
• An element Z(M) ∈ Z(∂M) associated to each oriented smooth (d + 1)-dimensional manifold (with boundary) M (corresponding to an additive axiom).

These data are subject to the following axioms (4 and 5 were added by Atiyah):

1. Z is functorial with respect to orientation preserving diffeomorphisms of Σ and M,
2. Z is involutory, i.e. Z(Σ*) = Z(Σ)* where Σ* is Σ with opposite orientation and Z(Σ)* denotes the dual module,
3. Z is multiplicative.
4. Z([math]\displaystyle{ \emptyset }[/math]) = Λ for the d-dimensional empty manifold and Z([math]\displaystyle{ \emptyset }[/math]) = 1 for the (d + 1)-dimensional empty manifold.
5. Z(M*) = Z(M) (the hermitian axiom). If [math]\displaystyle{ \partial M = \Sigma^*_0 \cup \Sigma_1 }[/math] so that Z(M) can be viewed as a linear transformation between hermitian vector spaces, then this is equivalent to Z(M*) being the adjoint of Z(M).

Remark. If for a closed manifold M we view Z(M) as a numerical invariant, then for a manifold with a boundary we should think of Z(M) ∈ Z(∂M) as a "relative" invariant. Let f : Σ → Σ be an orientation-preserving diffeomorphism, and identify opposite ends of Σ × I by f. This gives a manifold Σ_f and our axioms imply

[math]\displaystyle{ Z(\Sigma_f) = \operatorname{Trace}\ \Sigma(f) }[/math]

where Σ(f) is the induced automorphism of Z(Σ).

Remark. For a manifold M with boundary Σ we can always form the double [math]\displaystyle{ M\cup_\Sigma M^* }[/math] which is a closed manifold. The fifth axiom shows that

[math]\displaystyle{ Z\left(M\cup_\Sigma M^*\right) = |Z(M)|^2 }[/math]

where on the right we compute the norm in the hermitian (possibly indefinite) metric.

The relation to physics

Physically (2) + (4) are related to relativistic invariance while (3) + (5) are indicative of the quantum nature of the theory.

Σ is meant to indicate the physical space (usually, d = 3 for standard physics) and the extra dimension in Σ × I is "imaginary" time. The space Z(Σ) is the Hilbert space of the quantum theory and a physical theory, with a Hamiltonian H, will have a time evolution operator e^itH or an "imaginary time" operator e^−tH. The main feature of topological QFTs is that H = 0, which implies that there is no real dynamics or propagation, along the cylinder Σ × I. However, there can be non-trivial "propagation" (or tunneling amplitudes) from Σ₀ to Σ₁ through an intervening manifold M with [math]\displaystyle{ \partial M = \Sigma^*_0 \cup \Sigma_1 }[/math]; this reflects the topology of M.

If ∂M = Σ, then the distinguished vector Z(M) in the Hilbert space Z(Σ) is thought of as the vacuum state defined by M. For a closed manifold M the number Z(M) is the vacuum expectation value. In analogy with statistical mechanics it is also called the partition function.

The reason why a theory with a zero Hamiltonian can be sensibly formulated resides in the Feynman path integral approach to QFT. This incorporates relativistic invariance (which applies to general (d + 1)-dimensional "spacetimes") and the theory is formally defined by a suitable Lagrangian—a functional of the classical fields of the theory. A Lagrangian which involves only first derivatives in time formally leads to a zero Hamiltonian, but the Lagrangian itself may have non-trivial features which relate to the topology of M.

Atiyah's examples

In 1988, M. Atiyah published a paper in which he described many new examples of topological quantum field theory that were considered at that time (Atiyah 1988a)(Atiyah 1988b). It contains some new topological invariants along with some new ideas: Casson invariant, Donaldson invariant, Gromov's theory, Floer homology and Jones–Witten theory.

d = 0

In this case Σ consists of finitely many points. To a single point we associate a vector space V = Z(point) and to n-points the n-fold tensor product: V^⊗n = V ⊗ … ⊗ V. The symmetric group S_n acts on V^⊗n. A standard way to get the quantum Hilbert space is to start with a classical symplectic manifold (or phase space) and then quantize it. Let us extend S_n to a compact Lie group G and consider "integrable" orbits for which the symplectic structure comes from a line bundle, then quantization leads to the irreducible representations V of G. This is the physical interpretation of the Borel–Weil theorem or the Borel–Weil–Bott theorem. The Lagrangian of these theories is the classical action (holonomy of the line bundle). Thus topological QFT's with d = 0 relate naturally to the classical representation theory of Lie groups and the Symmetry group.

d = 1

We should consider periodic boundary conditions given by closed loops in a compact symplectic manifold X. Along with (Witten 1982) holonomy such loops as used in the case of d = 0 as a Lagrangian are then used to modify the Hamiltonian. For a closed surface M the invariant Z(M) of the theory is the number of pseudo holomorphic maps f : M → X in the sense of Gromov (they are ordinary holomorphic maps if X is a Kähler manifold). If this number becomes infinite i.e. if there are "moduli", then we must fix further data on M. This can be done by picking some points P_i and then looking at holomorphic maps f : M → X with f(P_i) constrained to lie on a fixed hyperplane. (Witten 1988b) has written down the relevant Lagrangian for this theory. Floer has given a rigorous treatment, i.e. Floer homology, based on Witten's Morse theory ideas; for the case when the boundary conditions are over the interval instead of being periodic, the path initial and end-points lie on two fixed Lagrangian submanifolds. This theory has been developed as Gromov–Witten invariant theory.

Another example is Holomorphic Conformal Field Theory. This might not have been considered strictly topological quantum field theory at the time because Hilbert spaces are infinite dimensional. The conformal field theories are also related to the compact Lie group G in which the classical phase consists of a central extension of the loop group (LG). Quantizing these produces the Hilbert spaces of the theory of irreducible (projective) representations of LG. The group Diff₊(S¹) now substitutes for the symmetric group and plays an important role. As a result, the partition function in such theories depends on complex structure, thus it is not purely topological.

d = 2

Jones–Witten theory is the most important theory in this case. Here the classical phase space, associated with a closed surface Σ is the moduli space of a flat G-bundle over Σ. The Lagrangian is an integer multiple of the Chern–Simons function of a G-connection on a 3-manifold (which has to be "framed"). The integer multiple k, called the level, is a parameter of the theory and k → ∞ gives the classical limit. This theory can be naturally coupled with the d = 0 theory to produce a "relative" theory. The details have been described by Witten who shows that the partition function for a (framed) link in the 3-sphere is just the value of the Jones polynomial for a suitable root of unity. The theory can be defined over the relevant cyclotomic field, see (Atiyah 1988). By considering a Riemann surface with boundary, we can couple it to the d = 1 conformal theory instead of coupling d = 2 theory to d = 0. This has developed into Jones–Witten theory and has led to the discovery of deep connections between knot theory and quantum field theory.

d = 3

Donaldson has defined the integer invariant of smooth 4-manifolds by using moduli spaces of SU(2)-instantons. These invariants are polynomials on the second homology. Thus 4-manifolds should have extra data consisting of the symmetric algebra of H₂. (Witten 1988a) has produced a super-symmetric Lagrangian which formally reproduces the Donaldson theory. Witten's formula might be understood as an infinite-dimensional analogue of the Gauss–Bonnet theorem. At a later date, this theory was further developed and became the Seiberg–Witten gauge theory which reduces SU(2) to U(1) in N = 2, d = 4 gauge theory. The Hamiltonian version of the theory has been developed by Floer in terms of the space of connections on a 3-manifold. Floer uses the Chern–Simons function, which is the Lagrangian of Jones–Witten theory to modify the Hamiltonian. For details, see (Atiyah 1988). (Witten 1988a) has also shown how one can couple the d = 3 and d = 1 theories together: this is quite analogous to the coupling between d = 2 and d = 0 in Jones–Witten theory.

Now, topological field theory is viewed as a functor, not on a fixed dimension but on all dimensions at the same time.

The case of a fixed spacetime

Let Bord_M be the category whose morphisms are n-dimensional submanifolds of M and whose objects are connected components of the boundaries of such submanifolds. Regard two morphisms as equivalent if they are homotopic via submanifolds of M, and so form the quotient category hBord_M: The objects in hBord_M are the objects of Bord_M, and the morphisms of hBord_M are homotopy equivalence classes of morphisms in Bord_M. A TQFT on M is a symmetric monoidal functor from hBord_M to the category of vector spaces.

Note that cobordisms can, if their boundaries match, be sewn together to form a new bordism. This is the composition law for morphisms in the cobordism category. Since functors are required to preserve composition, this says that the linear map corresponding to a sewn together morphism is just the composition of the linear map for each piece.

There is an equivalence of categories between the category of 2-dimensional topological quantum field theories and the category of commutative Frobenius algebras.

All n-dimensional spacetimes at once

The pair of pants is a (1+1)-dimensional bordism, which corresponds to a product or coproduct in a 2-dimensional TQFT.

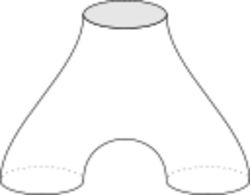
To consider all spacetimes at once, it is necessary to replace hBord_M by a larger category. So let Bord_n be the category of bordisms, i.e. the category whose morphisms are n-dimensional manifolds with boundary, and whose objects are the connected components of the boundaries of n-dimensional manifolds. (Note that any (n−1)-dimensional manifold may appear as an object in Bord_n.) As above, regard two morphisms in Bord_n as equivalent if they are homotopic, and form the quotient category hBord_n. Bord_n is a monoidal category under the operation which maps two bordisms to the bordism made from their disjoint union. A TQFT on n-dimensional manifolds is then a functor from hBord_n to the category of vector spaces, which maps disjoint unions of bordisms to their tensor product.

For example, for (1 + 1)-dimensional bordisms (2-dimensional bordisms between 1-dimensional manifolds), the map associated with a pair of pants gives a product or coproduct, depending on how the boundary components are grouped – which is commutative or cocommutative, while the map associated with a disk gives a counit (trace) or unit (scalars), depending on the grouping of boundary components, and thus (1+1)-dimension TQFTs correspond to Frobenius algebras.

Furthermore, we can consider simultaneously 4-dimensional, 3-dimensional and 2-dimensional manifolds related by the above bordisms, and from them we can obtain ample and important examples.

Development at a later time

Looking at the development of topological quantum field theory, we should consider its many applications to Seiberg–Witten gauge theory, topological string theory, the relationship between knot theory and quantum field theory, and quantum knot invariants. Furthermore, it has generated topics of great interest in both mathematics and physics. Also of important recent interest are non-local operators in TQFT ((Gukov Kapustin)). If string theory is viewed as the fundamental, then non-local TQFTs can be viewed as non-physical models that provide a computationally efficient approximation to local string theory.

Witten-type TQFTs and dynamical systems

Main page: Physics:Supersymmetric theory of stochastic dynamics

Stochastic (partial) differential equations (SDEs) are the foundation for models of everything in nature above the scale of quantum degeneracy and coherence and are essentially Witten-type TQFTs. All SDEs possess topological or BRST supersymmetry, [math]\displaystyle{ \delta }[/math], and in the operator representation of stochastic dynamics is the exterior derivative, which is commutative with the stochastic evolution operator. This supersymmetry preserves the continuity of phase space by continuous flows, and the phenomenon of supersymmetric spontaneous breakdown by a global non-supersymmetric ground state encompasses such well-established physical concepts as chaos, turbulence, 1/f and crackling noises, self-organized criticality etc. The topological sector of the theory for any SDE can be recognized as a Witten-type TQFT.

See also

• Quantum topology
• Topological defect
• Topological entropy in physics
• Topological order
• Topological quantum number
• Topological quantum computer
• Topological string theory
• Arithmetic topology
• Cobordism hypothesis

References

• Atiyah, Michael (1988a). "New invariants of three and four dimensional manifolds". The Mathematical Heritage of Hermann Weyl. Proceedings of Symposia in Pure Mathematics. 48. American Mathematical Society. pp. 285–299. doi:10.1090/pspum/048/974342. ISBN 9780821814826. https://archive.org/details/mathematicalheri0000symp/page/285. 
• Atiyah, Michael (1988b). "Topological quantum field theories". Publications Mathématiques de l'IHÉS 68 (68): 175–186. doi:10.1007/BF02698547. http://www.math.ru.nl/~mueger/TQFT/At.pdf. 
• Gukov, Sergei; Kapustin, Anton (2013). "Topological Quantum Field Theory, Nonlocal Operators, and Gapped Phases of Gauge Theories". arXiv:1307.4793 [hep-th].
• Linker, Patrick (2015). "Topological Dipole Field Theory". The Winnower 2: e144311.19292. doi:10.15200/winn.144311.19292. https://tuprints.ulb.tu-darmstadt.de/4981/1/2658-topological-dipole-field-theory%20%281%29.pdf. 
• Lurie, Jacob (2009). "On the Classification of Topological Field Theories". arXiv:0905.0465 [math.CT].
• Schwarz, Albert (2000). "Topological quantum field theories". arXiv:hep-th/0011260.
• Segal, Graeme (2001). "Topological structures in string theory". Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences 359 (1784): 1389–1398. doi:10.1098/rsta.2001.0841. Bibcode: 2001RSPTA.359.1389S. 
• Witten, Edward (1982). "Super-symmetry and Morse Theory". Journal of Differential Geometry 17 (4): 661–692. doi:10.4310/jdg/1214437492. 
• Witten, Edward (1988a). "Topological quantum field theory". Communications in Mathematical Physics 117 (3): 353–386. doi:10.1007/BF01223371. Bibcode: 1988CMaPh.117..353W. http://projecteuclid.org/euclid.cmp/1104161738. 
• Witten, Edward (1988b). "Topological sigma models". Communications in Mathematical Physics 118 (3): 411–449. doi:10.1007/bf01466725. Bibcode: 1988CMaPh.118..411W. http://projecteuclid.org/DPubS/Repository/1.0/Disseminate?view=body&id=pdf_1&handle=euclid.cmp/1104162092. 

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Topological quantum field theory. Read more