Unilateral contact

In contact mechanics, the term unilateral contact, also called unilateral constraint, denotes a mechanical constraint which prevents penetration between two rigid/flexible bodies. Constraints of this kind are omnipresent in non-smooth multibody dynamics applications, such as granular flows,^[1] legged robot, vehicle dynamics, particle damping, imperfect joints,^[2] or rocket landings. In these applications, the unilateral constraints result in impacts happening, therefore requiring suitable methods to deal with such constraints.

Modelling of the unilateral constraints

There are mainly two kinds of methods to model the unilateral constraints. The first kind is based on smooth contact dynamics, including methods using Hertz's models, penalty methods, and some regularization force models, while the second kind is based on the non-smooth contact dynamics, which models the system with unilateral contacts as variational inequalities.

Smooth contact dynamics

See also: Contact mechanics

Hertz contact model

In this method, normal forces generated by the unilateral constraints are modelled according to the local material properties of bodies. In particular, contact force models are derived from continuum mechanics, and expressed as functions of the gap and the impact velocity of bodies. As an example, an illustration of the classic Hertz contact model is shown in the figure on the right. In such model, the contact is explained by the local deformation of bodies. More contact models can be found in some review scientific works^[3][4][5] or in the article dedicated to contact mechanics.

Non-smooth contact dynamics

In non-smooth method, unilateral interactions between bodies are fundamentally modelled by the Signorini condition^[6] for non-penetration, and impact laws are used to define the impact process.^[7] The Signorini condition can be expressed as the complementarity problem:

[math]\displaystyle{ g \geq 0, \quad \lambda \geq 0, \quad \lambda \perp g }[/math],

where [math]\displaystyle{ g }[/math] denotes the distance between two bodies and [math]\displaystyle{ \lambda }[/math] denotes the contact force generated by the unilateral constraints, as shown in the figure below. Moreover, in terms of the concept of proximal point of convex theory, the Signorini condition can be equivalently expressed^[6][8] as:

[math]\displaystyle{ \lambda ={\rm{proj}}_{\R^+}(\lambda -\rho g ) }[/math],

where [math]\displaystyle{ \rho\gt 0 }[/math] denotes an auxiliary parameter, and [math]\displaystyle{ {\rm proj}_{\bf C}(x) }[/math] represents the proximal point in the set [math]\displaystyle{ C }[/math] to the variable [math]\displaystyle{ x }[/math],^[9] defined as:

[math]\displaystyle{ {\rm proj}_{\bf C}(x)={\rm argmin}_{y\in C}\|y-x\| }[/math].

Both the expressions above represent the dynamic behaviour of unilateral constraints: on the one hand, when the normal distance [math]\displaystyle{ g_{\rm N} }[/math] is above zero, the contact is open, which means that there is no contact force between bodies, [math]\displaystyle{ \lambda =0 }[/math]; on the other hand, when the normal distance [math]\displaystyle{ g_{\rm N} }[/math] is equal to zero, the contact is closed, resulting in [math]\displaystyle{ \lambda \geq0 }[/math].

Figure 2: a) unilateral contact, b) the Signorini graph, c) continuum mechanics based model

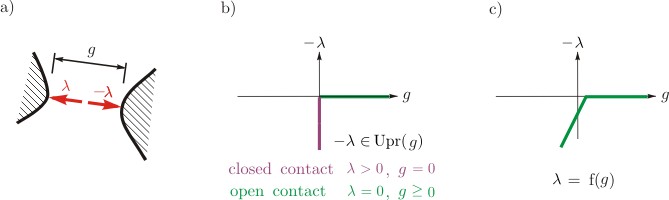
When implementing non-smooth theory based methods, the velocity Signorini condition or the acceleration Signorini condition are actually employed in most cases. The velocity Signorini condition is expressed as:^[6][10]

[math]\displaystyle{ U_{\rm N}^{+}\geq 0,\quad \lambda \geq0,\quad U^{+}\lambda =0 }[/math],

where [math]\displaystyle{ U_{\rm N}^{+} }[/math] denotes the relative normal velocity after impact. The velocity Signorini condition should be understood together with the previous conditions [math]\displaystyle{ g \geq 0,\;\lambda \geq 0,\;\lambda \perp g }[/math]. The acceleration Signorini condition is considered under closed contact ([math]\displaystyle{ g =0, U_{\rm N}^{+}=0 }[/math]), as:^[8]

[math]\displaystyle{ \ddot g \geq 0,\quad \lambda \geq0,\quad \ddot g \lambda =0 }[/math],

where the overdots denote the second-order derivative with respect to time.

When using this method for unilateral constraints between two rigid bodies, the Signorini condition alone is not enough to model the impact process, so impact laws, which give the information about the states before and after the impact,^[6] are also required. For example, when the Newton restitution law is employed, a coefficient of restitution will be defined as: [math]\displaystyle{ e=-{U_{\rm N}^{+}}/{U_{\rm N}^{-}} }[/math], where [math]\displaystyle{ U_{\rm N}^{-} }[/math]denotes the relative normal velocity before impact.

Frictional unilateral constraints

For frictional unilateral constraints, the normal contact forces are modelled by one of the methods above, while the friction forces are commonly described by means of Coulomb's friction law. Coulomb's friction law can be expressed as follows: when the tangential velocity [math]\displaystyle{ U_{\rm T} }[/math] is not equal to zero, namely when the two bodies are sliding, the friction force [math]\displaystyle{ \lambda_{\rm T} }[/math] is proportional to the normal contact force [math]\displaystyle{ \lambda }[/math]; when instead the tangential velocity [math]\displaystyle{ U_{\rm T} }[/math] is equal to zero, namely when the two bodies are relatively steady, the friction force [math]\displaystyle{ \lambda_{\rm T} }[/math] is no more than the maximum of the static friction force. This relationship can be summarised using the maximum dissipation principle,^[6] as

[math]\displaystyle{ \lambda_{\rm T} \in D(\mu \lambda)~~~~~~\forall S\in D(\mu \lambda)~~~~~~(S-\lambda_{\rm T})U_{\rm T}\geq 0, }[/math]

where

[math]\displaystyle{ D(\mu \lambda)=\{\forall x|-\mu \lambda\leq\|x\|\leq \mu \lambda\} }[/math]

represents the friction cone, and [math]\displaystyle{ \mu }[/math] denotes the kinematic friction coefficient. Similarly to the normal contact force, the formulation above can be equivalently expressed in terms of the notion of proximal point as:^[6]

[math]\displaystyle{ \lambda_{\rm T}={\rm{proj}}_{D(\mu\lambda)}(\lambda_T-\rho U_{\rm T}) }[/math],

where [math]\displaystyle{ \rho\gt 0 }[/math] denotes an auxiliary parameter.

Solution techniques

If the unilateral constraints are modelled by the continuum mechanics based contact models, the contact forces can be computed directly through an explicit mathematical formula, that depends on the contact model of choice. If instead the non-smooth theory based method is employed, there are two main formulations for the solution of the Signorini conditions: the nonlinear/linear complementarity problem (N/LCP) formulation and the augmented Lagrangian formulation. With respect to the solution of contact models, the non-smooth method is more tedious, but less costly from the computational viewpoint. A more detailed comparison of solution methods using contact models and non-smooth theory was carried out by Pazouki et al.^[11]

N/LCP formulations

Following this approach, the solution of dynamics equations with unilateral constraints is transformed into the solution of N/LCPs. In particular, for frictionless unilateral constraints or unilateral constraints with planar friction, the problem is transformed into LCPs, while for frictional unilateral constraints, the problem is transformed into NCPs. To solve LCPs, the pivoting algorithm, originating from the algorithm of Lemek and Dantzig, is the most popular method.^[8] Unfortunately, however, numerical experiments show that the pivoting algorithm may fail when handling systems with a large number of unilateral contacts, even using the best optimizations.^[12] For NCPs, using a polyhedral approximation can transform the NCPs into a set of LCPs, which can then be solved by the LCP solver.^[13] Other approaches beyond these methods, such NCP-functions^[14][15][16] or cone complementarity problems (CCP) based methods^[17][18] are also employed to solve NCPs.

Augmented Lagrangian formulation

Different from the N/LCP formulations, the augmented Lagrangian formulation uses the proximal functions described above, [math]\displaystyle{ \lambda={\rm{proj}}_{\R^+}(\lambda-\rho g) }[/math]. Together with dynamics equations, this formulation is solved by means of root-finding algorithms. A comparative study between LCP formulations and the augmented Lagrangian formulation was carried out by Mashayekhi et al.^[9]

See also

• Physics:Contact dynamics – Motion of multibody systems
• Physics:Contact mechanics – Study of the deformation of solids that touch each other
• Discrete element method – Numerical methods for computing the motion and effect of a large number of small particles
• Physics:Non-smooth mechanics – Modeling approach in mechanics
• Collision response
• Variational inequalities

References

Further reading

Open-source software

Open-source codes and non-commercial packages using the non-smooth based method:

• Software:Siconos – Open source scientific software for modeling non-smooth dynamical systems
• Chrono, an open source multi-physics simulation engine, see also project website

Books and articles

• Acary V., Brogliato B. Numerical Methods for Nonsmooth Dynamical Systems. Applications in Mechanics and Electronics. Springer Verlag, LNACM 35, Heidelberg, 2008.
• Brogliato B. Nonsmooth Mechanics. Communications and Control Engineering Series Springer-Verlag, London, 1999 (2dn Ed.)
• Demyanov, V.F., Stavroulakis, G.E., Polyakova, L.N., Panagiotopoulos, P.D. "Quasidifferentiability and Nonsmooth Modelling in Mechanics, Engineering and Economics" Springer 1996
• Glocker, Ch. Dynamik von Starrkoerpersystemen mit Reibung und Stoessen, volume 18/182 of VDI Fortschrittsberichte Mechanik/Bruchmechanik. VDI Verlag, Düsseldorf, 1995
• Glocker Ch. and Studer C. Formulation and preparation for Numerical Evaluation of Linear Complementarity Systems. Multibody System Dynamics 13(4):447-463, 2005
• Jean M. The non-smooth contact dynamics method. Computer Methods in Applied mechanics and Engineering 177(3-4):235-257, 1999
• Moreau J.J. Unilateral Contact and Dry Friction in Finite Freedom Dynamics, volume 302 of Non-smooth Mechanics and Applications, CISM Courses and Lectures. Springer, Wien, 1988
• Pfeiffer F., Foerg M. and Ulbrich H. Numerical aspects of non-smooth multibody dynamics. Comput. Methods Appl. Mech. Engrg 195(50-51):6891-6908, 2006
• Potra F.A., Anitescu M., Gavrea B. and Trinkle J. A linearly implicit trapezoidal method for integrating stiff multibody dynamics with contacts, joints and friction. Int. J. Numer. Meth. Engng 66(7):1079-1124, 2006
• Stewart D.E. and Trinkle J.C. An Implicit Time-Stepping Scheme for Rigid Body Dynamics with Inelastic Collisions and Coulomb Friction. Int. J. Numer. Methods Engineering 39(15):2673-2691, 1996
• Studer C. Augmented time-stepping integration of non-smooth dynamical systems, PhD Thesis ETH Zurich, ETH E-Collection, to appear 2008
• Studer C. Numerics of Unilateral Contacts and Friction -- Modeling and Numerical Time Integration in Non-Smooth Dynamics, Lecture Notes in Applied and Computational Mechanics, Volume 47, Springer, Berlin, Heidelberg, 2009

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Unilateral contact. Read more