Rectifier (neural networks)
 From HandWiki - Reading time: 11 min
From HandWiki - Reading time: 11 min
| Machine learning and data mining |
|---|
 |

In the context of artificial neural networks, the rectifier or ReLU (rectified linear unit) activation function[1][2] is an activation function defined as the non-negative part of its argument, i.e., the ramp function:
where is the input to a neuron. This is analogous to half-wave rectification in electrical engineering.
ReLU is one of the most popular activation functions for artificial neural networks,[3] and finds application in computer vision[4] and speech recognition[5][6] using deep neural nets and computational neuroscience.[7][8]
History
The ReLU was first used by Alston Householder in 1941 as a mathematical abstraction of biological neural networks.[9]
Kunihiko Fukushima in 1969 used ReLU in the context of visual feature extraction in hierarchical neural networks.[10][11] Thirty years later, Hahnloser et al. argued that ReLU approximates the biological relationship between neural firing rates and input current, in addition to enabling recurrent neural network dynamics to stabilise under weaker criteria.[12][13]
Prior to 2010, most activation functions used were the logistic sigmoid (which is inspired by probability theory; see logistic regression) and its more numerically efficient[14] counterpart, the hyperbolic tangent. Around 2010, the use of ReLU became common again.
Jarrett et al. (2009) noted that rectification by either absolute or ReLU (which they called "positive part") was critical for object recognition in convolutional neural networks (CNNs), specifically because it allows average pooling without neighboring filter outputs cancelling each other out. They hypothesized that the use of sigmoid or tanh was responsible for poor performance in previous CNNs.[15]
Nair and Hinton (2010) made a theoretical argument that the softplus activation function should be used, in that the softplus function numerically approximates the sum of an exponential number of linear models that share parameters. They then proposed ReLU as a good approximation to it. Specifically, they began by considering a single binary neuron in a Boltzmann machine that takes as input, and produces 1 as output with probability . They then considered extending its range of output by making infinitely many copies of it , that all take the same input, offset by an amount , then their outputs are added together as . They then demonstrated that is approximately equal to , which is also approximately equal to , where stands for the gaussian distribution.
They also argued for another reason for using ReLU: that it allows "intensity equivariance" in image recognition. That is, multiplying input image by a constant multiplies the output also. In contrast, this is false for other activation functions like sigmoid or tanh. They found that ReLU activation allowed good empirical performance in restricted Boltzmann machines.[16]
Glorot et al (2011) argued that ReLU has the following advantages over sigmoid or tanh. ReLU is more similar to biological neurons' responses in their main operating regime. ReLU avoids vanishing gradients. ReLU is cheaper to compute. ReLU creates sparse representation naturally, because many hidden units output exactly zero for a given input. They also found empirically that deep networks trained with ReLU can achieve strong performance without unsupervised pre-training, especially on large, purely supervised tasks.[4]
Advantages
Advantages of ReLU include:
- Sparse activation: for example, in a randomly initialized network, only about 50% of hidden units are activated (i.e. have a non-zero output).
- Better gradient propagation: fewer vanishing gradient problems compared to sigmoidal activation functions that saturate in both directions.[4]
- Efficiency: only requires comparison and addition.
- Scale-invariant (homogeneous, or "intensity equivariance"[16]):
- .
Potential problems
Possible downsides can include:
- Non-differentiability at zero (however, it is differentiable anywhere else, and the value of the derivative at zero can be chosen to be 0 or 1 arbitrarily).
- ReLU is unbounded.
- Redundancy of the parametrization: Because ReLU is scale-invariant, the network computes the exact same function by scaling the weights and biases in front of a ReLU activation by , and the weights after by .[4]
- Dying ReLU: ReLU neurons can sometimes be pushed into states in which they become inactive for essentially all inputs. In this state, no gradients flow backward through the neuron, and so the neuron becomes stuck in a perpetually inactive state (it "dies"). This is a form of the vanishing gradient problem. In some cases, large numbers of neurons in a network can become stuck in dead states, effectively decreasing the model capacity and potentially even halting the learning process. This problem typically arises when the learning rate is set too high. It may be mitigated by using "leaky" ReLU instead, where a small positive slope is assigned for . However, depending on the task, performance may be reduced.
Variants
Piecewise-linear variants
Leaky ReLU (2014) allows a small, positive gradient when the unit is inactive,[6] helping to mitigate the vanishing gradient problem. This gradient is defined by a parameter , typically set to 0.01–0.3.[17][18]
The same function can also be expressed without the piecewise notation as:
Parametric ReLU (PReLU, 2016) takes this idea further by making a learnable parameter along with the other network parameters.[19]
Note that for , this is equivalent to
and thus has a relation to "maxout" networks.[19]
Concatenated ReLU (CReLU, 2016) preserves positive and negative phase information by returning two values:[20]
Smooth variants
Softplus

A smooth approximation to the rectifier is the analytic function
which is called the softplus (2000)[21][4] or SmoothReLU function.[22] For large negative it is roughly , so just above 0, while for large positive it is roughly , so just above .
This function can be approximated as:
By making the change of variables , this is equivalent to
A sharpness parameter may be included:
The derivative of softplus is the logistic function. This in turn can be viewed as a smooth approximation of the derivative of the rectifier, the Heaviside step function.
The multivariable generalization of single-variable softplus is the LogSumExp with the first argument set to zero:
The LogSumExp function is
and its gradient is the softmax; the softmax with the first argument set to zero is the multivariable generalization of the logistic function. Both LogSumExp and softmax are used in machine learning.
ELU
Exponential linear units (2015) smoothly allow negative values. This is an attempt to make the mean activations closer to zero, which speeds up learning. It has been shown that ELUs can obtain higher classification accuracy than ReLUs.[23]
In these formulas, is a hyperparameter to be tuned with the constraint .
Given the same interpretation of , ELU can be viewed as a smoothed version of a shifted ReLU (SReLU), which has the form .
Gaussian-error linear unit (GELU)
GELU (2016) is a smooth approximation to the rectifier:
where is the cumulative distribution function of the standard normal distribution.
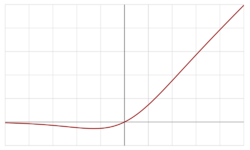
This activation function is illustrated in the figure at the start of this article. It has a "bump" with negative derivative to the left of x < 0. It serves as the default activation for many transformer models such as BERT.[24]
SiLU
The SiLU (sigmoid linear unit) or swish function[25] is another smooth approximation which uses the sigmoid (logistic) function, first introduced in the 2016 GELU paper:[24]
It is cheaper to calculate than GELU. It also has a "bump".
Mish
The mish function (2019) can also be used as a smooth approximation of the rectifier.[25] It is defined as
where is the hyperbolic tangent, and is the softplus function.
Mish was obtained by experimenting with functions similar to Swish (SiLU, see above). It is non-monotonic (has a "bump") like Swish. The main new feature is that it exhibits a "self-regularizing" behavior attributed to a term in its first derivative.[25][26]
Squareplus
Squareplus (2021)[27] is the function
where is a hyperparameter that determines the "size" of the curved region near . (For example, letting yields ReLU, and letting yields the metallic mean function.) Squareplus shares many properties with softplus: It is monotonic, strictly positive, approaches 0 as , approaches the identity as , and is smooth. However, squareplus can be computed using only algebraic functions, making it well-suited for settings where computational resources or instruction sets are limited. Additionally, squareplus requires no special consideration to ensure numerical stability when is large.
DELU
ExtendeD Exponential Linear Unit (DELU, 2023) is an activation function which is smoother within the neighborhood of zero and sharper for bigger values, allowing better allocation of neurons in the learning process for higher performance. Thanks to its unique design, it has been shown that DELU may obtain higher classification accuracy than ReLU and ELU.[28]
In these formulas, , and are hyperparameter values which could be set as default constraints , and , as done in the original work.
See also
References
- ↑ Brownlee, Jason (8 January 2019). "A Gentle Introduction to the Rectified Linear Unit (ReLU)". https://machinelearningmastery.com/rectified-linear-activation-function-for-deep-learning-neural-networks/.
- ↑ Liu, Danqing (30 November 2017). "A Practical Guide to ReLU" (in en). https://medium.com/@danqing/a-practical-guide-to-relu-b83ca804f1f7.
- ↑ Ramachandran, Prajit; Barret, Zoph; Quoc, V. Le (October 16, 2017). "Searching for Activation Functions". arXiv:1710.05941 [cs.NE].
- ↑ 4.0 4.1 4.2 4.3 4.4 Xavier Glorot; Antoine Bordes; Yoshua Bengio (2011). "Deep sparse rectifier neural networks". AISTATS. https://proceedings.mlr.press/v15/glorot11a/glorot11a.pdf. "Rectifier and softplus activation functions. The second one is a smooth version of the first."
- ↑ László Tóth (2013). "Phone Recognition with Deep Sparse Rectifier Neural Networks". ICASSP. http://www.inf.u-szeged.hu/~tothl/pubs/ICASSP2013.pdf.
- ↑ 6.0 6.1 Andrew L. Maas, Awni Y. Hannun, Andrew Y. Ng (2014). Rectifier Nonlinearities Improve Neural Network Acoustic Models.
- ↑ Hansel, D.; van Vreeswijk, C. (2002). "How noise contributes to contrast invariance of orientation tuning in cat visual cortex". J. Neurosci. 22 (12): 5118–5128. doi:10.1523/JNEUROSCI.22-12-05118.2002. PMID 12077207.
- ↑ Kadmon, Jonathan; Sompolinsky, Haim (2015-11-19). "Transition to Chaos in Random Neuronal Networks". Physical Review X 5 (4): 041030. doi:10.1103/PhysRevX.5.041030. Bibcode: 2015PhRvX...5d1030K.
- ↑ Householder, Alston S. (June 1941). "A theory of steady-state activity in nerve-fiber networks: I. Definitions and preliminary lemmas" (in en). The Bulletin of Mathematical Biophysics 3 (2): 63–69. doi:10.1007/BF02478220. ISSN 0007-4985. http://link.springer.com/10.1007/BF02478220.
- ↑ Fukushima, K. (1969). "Visual feature extraction by a multilayered network of analog threshold elements". IEEE Transactions on Systems Science and Cybernetics 5 (4): 322–333. doi:10.1109/TSSC.1969.300225.
- ↑ Fukushima, K.; Miyake, S. (1982). "Neocognitron: A Self-Organizing Neural Network Model for a Mechanism of Visual Pattern Recognition". Competition and Cooperation in Neural Nets. Lecture Notes in Biomathematics. 45. Springer. pp. 267–285. doi:10.1007/978-3-642-46466-9_18. ISBN 978-3-540-11574-8.
- ↑ Hahnloser, R.; Sarpeshkar, R.; Mahowald, M. A.; Douglas, R. J.; Seung, H. S. (2000). "Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit". Nature 405 (6789): 947–951. doi:10.1038/35016072. PMID 10879535. Bibcode: 2000Natur.405..947H.
- ↑ Hahnloser, Richard; Seung, H. Sebastian (2000). "Permitted and Forbidden Sets in Symmetric Threshold-Linear Networks". Advances in Neural Information Processing Systems (MIT Press) 13. https://proceedings.neurips.cc/paper/2000/hash/c8cbd669cfb2f016574e9d147092b5bb-Abstract.html.
- ↑ Yann LeCun; Leon Bottou; Genevieve B. Orr; Klaus-Robert Müller (1998). "Efficient BackProp". Neural Networks: Tricks of the Trade. Springer. http://yann.lecun.com/exdb/publis/pdf/lecun-98b.pdf.
- ↑ Jarrett, Kevin; Kavukcuoglu, Koray; Ranzato, Marc'Aurelio; LeCun, Yann (September 2009). "What is the best multi-stage architecture for object recognition?". 2009 IEEE 12th International Conference on Computer Vision. pp. 2146–2153. doi:10.1109/ICCV.2009.5459469. ISBN 978-1-4244-4420-5. https://ieeexplore.ieee.org/document/5459469.
- ↑ 16.0 16.1 Nair, Vinod, and Geoffrey E. Hinton. "Rectified linear units improve restricted boltzmann machines." Proceedings of the 27th international conference on machine learning (ICML-10). 2010.
- ↑ "PyTorch Leaky ReLU docs". https://pytorch.org/docs/stable/generated/torch.nn.LeakyReLU.html.
- ↑ "TensorFlow Leaky ReLU docs". https://www.tensorflow.org/api_docs/python/tf/keras/layers/LeakyReLU.
- ↑ 19.0 19.1 He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian (2015). "Delving Deep into Rectifiers: Surpassing Human-Level Performance on Image Net Classification". arXiv:1502.01852 [cs.CV].
- ↑ Shang, Wenling; Sohn, Kihyuk; Almeida, Diogo; Lee, Honglak (2016-06-11). "Understanding and Improving Convolutional Neural Networks via Concatenated Rectified Linear Units" (in en). Proceedings of the 33rd International Conference on Machine Learning (PMLR): 2217–2225. https://proceedings.mlr.press/v48/shang16.html.
- ↑ Dugas, Charles; Bengio, Yoshua; Bélisle, François; Nadeau, Claude; Garcia, René (2000-01-01). "Incorporating second-order functional knowledge for better option pricing". Proceedings of the 13th International Conference on Neural Information Processing Systems (NIPS'00) (MIT Press): 451–457. http://papers.nips.cc/paper/1920-incorporating-second-order-functional-knowledge-for-better-option-pricing.pdf. "Since the sigmoid h has a positive first derivative, its primitive, which we call softplus, is convex.".
- ↑ "Smooth Rectifier Linear Unit (SmoothReLU) Forward Layer" (in en-US). 2017. https://software.intel.com/sites/products/documentation/doclib/daal/daal-user-and-reference-guides/daal_prog_guide/GUID-FAC73B9B-A597-4F7D-A5C4-46707E4A92A0.htm.
- ↑ Clevert, Djork-Arné; Unterthiner, Thomas; Hochreiter, Sepp (2015). "Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs)". arXiv:1511.07289 [cs.LG].
- ↑ 24.0 24.1 Hendrycks, Dan; Gimpel, Kevin (2016). "Gaussian Error Linear Units (GELUs)". arXiv:1606.08415 [cs.LG].
- ↑ 25.0 25.1 25.2 Diganta Misra (23 Aug 2019), Mish: A Self Regularized Non-Monotonic Activation Function, https://www.bmvc2020-conference.com/assets/papers/0928.pdf, retrieved 26 March 2022.
- ↑ Shaw, Sweta (2020-05-10). "Activation Functions Compared with Experiments" (in en). https://wandb.ai/shweta/Activation%20Functions/reports/Activation-Functions-Compared-with-Experiments--VmlldzoxMDQwOTQ.
- ↑ Barron, Jonathan T. (22 December 2021). "Squareplus: A Softplus-Like Algebraic Rectifier". arXiv:2112.11687 [cs.NE].
- ↑ Çatalbaş, Burak; Morgül, Ömer (16 August 2023). "Deep learning with ExtendeD Exponential Linear Unit (DELU)". Neural Computing and Applications 35 (30): 22705–22724. doi:10.1007/s00521-023-08932-z. https://link.springer.com/article/10.1007/s00521-023-08932-z. Retrieved 20 April 2025.
Template:Artificial intelligence navbox
 KSF
KSF