Regular graph

In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each internal vertex are equal to each other.^[1] A regular graph with vertices of degree k is called a k‑regular graph or regular graph of degree k.

Template:Tocleft

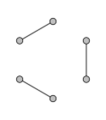
Regular graphs of degree at most 2 are easy to classify: a 0-regular graph consists of disconnected vertices, a 1-regular graph consists of disconnected edges, and a 2-regular graph consists of a disjoint union of cycles and infinite chains.

In analogy with the terminology for polynomials of low degrees, a 3-regular or 4-regular graph often is called a cubic graph or a quartic graph, respectively. Similarly, it is possible to denote k-regular graphs with ${\displaystyle k=5,6,7,8,\dots }$ as quintic, sextic, septic, octic, et cetera.

A strongly regular graph is a regular graph where every adjacent pair of vertices has the same number l of neighbors in common, and every non-adjacent pair of vertices has the same number n of neighbors in common. The smallest graphs that are regular but not strongly regular are the cycle graph and the circulant graph on 6 vertices.

The complete graph K_m is strongly regular for any m.

• 
  0-regular graph
• 
  1-regular graph
• 
  2-regular graph
• 
  3-regular graph

By the degree sum formula, a k-regular graph with n vertices has ${\displaystyle \frac{nk}{2}}$ edges. In particular, at least one of the order n and the degree k must be an even number.

A theorem by Nash-Williams says that every k‑regular graph on 2k + 1 vertices has a Hamiltonian cycle.

Let A be the adjacency matrix of a graph. Then the graph is regular if and only if ${\displaystyle \text{j}=(1,\dots ,1)}$ is an eigenvector of A.^[2] Its eigenvalue will be the constant degree of the graph. Eigenvectors corresponding to other eigenvalues are orthogonal to ${\displaystyle \text{j}}$, so for such eigenvectors ${\displaystyle v=(v_1,\dots ,v_n)}$, we have ${\displaystyle {\displaystyle \sum _{i=1}^n}{v}_i=0}$.

A regular graph of degree k is connected if and only if the eigenvalue k has multiplicity one. The "only if" direction is a consequence of the Perron–Frobenius theorem.^[2]

There is also a criterion for regular and connected graphs : a graph is connected and regular if and only if the matrix of ones J, with ${\displaystyle J_{ij}=1}$, is in the adjacency algebra of the graph (meaning it is a linear combination of powers of A).^[3]

Let G be a k-regular graph with diameter D and eigenvalues of adjacency matrix ${\displaystyle k={\lambda }_0>{\lambda }_1\ge \cdots \ge {\lambda }_{n-1}}$. If G is not bipartite, then

${\displaystyle D\le \frac{\log (n-1)}{\log ({\lambda }_0/{\lambda }_1)}+1.}$^[4]

There exists a ${\displaystyle k}$-regular graph of order ${\displaystyle n}$ if and only if the natural numbers n and k satisfy the inequality ${\displaystyle n\ge k+1}$ and that ${\displaystyle nk}$ is even.

Proof: If a graph with n vertices is k-regular, then the degree k of any vertex v cannot exceed the number ${\displaystyle n-1}$ of vertices different from v, and indeed at least one of n and k must be even, whence so is their product.

Conversely, if n and k are two natural numbers satisfying both the inequality and the parity condition, then indeed there is a k-regular circulant graph ${\displaystyle C_n^{s_1,\dots ,s_r}}$ of order n (where the ${\displaystyle s_i}$ denote the minimal `jumps' such that vertices with indices differing by an ${\displaystyle s_i}$ are adjacent). If in addition k is even, then ${\displaystyle k=2r}$, and a possible choice is ${\displaystyle (s_1,\dots ,s_r)=(1,2,\dots ,r)}$. Else k is odd, whence n must be even, say with ${\displaystyle n=2m}$, and then ${\displaystyle k=2r-1}$ and the `jumps' may be chosen as ${\displaystyle (s_1,\dots ,s_r)=(1,2,\dots ,r-1,m)}$.

If ${\displaystyle n=k+1}$, then this circulant graph is complete.

Fast algorithms exist to generate, up to isomorphism, all regular graphs with a given degree and number of vertices.^[5]

• Random regular graph
• Strongly regular graph
• Moore graph
• Cage graph
• Highly irregular graph

• Weisstein, Eric W.. "Regular Graph". http://mathworld.wolfram.com/RegularGraph.html. 
• Weisstein, Eric W.. "Strongly Regular Graph". http://mathworld.wolfram.com/StronglyRegularGraph.html. 
• GenReg software and data by Markus Meringer.
• Nash-Williams, Crispin (1969), Valency Sequences which force graphs to have Hamiltonian Circuits, University of Waterloo Research Report, Waterloo, Ontario: University of Waterloo 

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Regular graph. Read more