Table of Contents Categories
  Encyclosphere.org ENCYCLOREADER
  supported by EncyclosphereKSF

Set (mathematics)

From HandWiki - Reading time: 18 min
Short description: Collection of mathematical objects
A set of polygons in an Euler diagram
This set equals the one depicted above since both have the very same elements.

A set is the mathematical model for a collection of different[1] things;[2][3][4] a set contains elements or members, which can be mathematical objects of any kind: numbers, symbols, points in space, lines, other geometrical shapes, variables, or even other sets.[5] The set with no elements is the empty set; a set with a single element is a singleton. A set may have a finite number of elements or be an infinite set.

Sets are uniquely characterized by their elements; this means that two sets that have precisely the same elements are equal (they are the same set).[6] This property is called extensionality. In particular, this implies that there is only one empty set.

Sets are ubiquitous in modern mathematics. Indeed, set theory, more specifically Zermelo–Fraenkel set theory, has been the standard way to provide rigorous foundations for all branches of mathematics since the first half of the 20th century.[5]

Definition and notation

Mathematical texts commonly denote sets by capital letters[7][5] in italic, such as A, B, C.[8] A set may also be called a collection or family, especially when its elements are themselves sets.

Roster notation

Roster or enumeration notation defines a set by listing its elements between curly brackets, separated by commas:[9][10][11][12]

A = {4, 2, 1, 3}
B = {blue, white, red}.

This notation was introduced by Ernst Zermelo in 1908.[13] In a set, all that matters is whether each element is in it or not, so the ordering of the elements in roster notation is irrelevant (in contrast, in a sequence, a tuple, or a permutation of a set, the ordering of the terms matters). For example, {2, 4, 6} and {4, 6, 4, 2} represent the same set.[14][8][15]

For sets with many elements, especially those following an implicit pattern, the list of members can be abbreviated using an ellipsis '...'.[16][17] For instance, the set of the first thousand positive integers may be specified in roster notation as

{1, 2, 3, ..., 1000}.

Infinite sets in roster notation

An infinite set is a set with an endless list of elements. To describe an infinite set in roster notation, an ellipsis is placed at the end of the list, or at both ends, to indicate that the list continues forever. For example, the set of nonnegative integers is

{0, 1, 2, 3, 4, ...},

and the set of all integers is

{..., −3, −2, −1, 0, 1, 2, 3, ...}.

Semantic definition

Another way to define a set is to use a rule to determine what the elements are:

Let A be the set whose members are the first four positive integers.
Let B be the set of colors of the French flag.

Such a definition is called a semantic description.[18][19]

Set-builder notation

Main page: Set-builder notation

Set-builder notation specifies a set as a selection from a larger set, determined by a condition on the elements.[19][20][21] For example, a set F can be defined as follows:

[math]\displaystyle{ F = \{n \mid n \text{ is an integer, and } 0 \leq n \leq 19\}. }[/math]

In this notation, the vertical bar "|" means "such that", and the description can be interpreted as "F is the set of all numbers n such that n is an integer in the range from 0 to 19 inclusive". Some authors use a colon ":" instead of the vertical bar.[22]

Classifying methods of definition

Philosophy uses specific terms to classify types of definitions:

  • An intensional definition uses a rule to determine membership. Semantic definitions and definitions using set-builder notation are examples.
  • An extensional definition describes a set by listing all its elements.[19] Such definitions are also called enumerative.
  • An ostensive definition is one that describes a set by giving examples of elements; a roster involving an ellipsis would be an example.

Membership

Main page: Element (mathematics)

If B is a set and x is an element of B, this is written in shorthand as x ∈ B, which can also be read as "x belongs to B", or "x is in B".[23] The statement "y is not an element of B" is written as y ∉ B, which can also be read as "y is not in B".[24][25]

For example, with respect to the sets A = {1, 2, 3, 4}, B = {blue, white, red}, and F = {n | n is an integer, and 0 ≤ n ≤ 19},

4 ∈ A and 12 ∈ F; and
20 ∉ F and green ∉ B.

The empty set

Main page: Empty set

The empty set (or null set) is the unique set that has no members. It is denoted ∅, [math]\displaystyle{ \emptyset }[/math], { },[26][27] ϕ,[28] or ϕ.[29]

Singleton sets

Main page: Singleton (mathematics)

A singleton set is a set with exactly one element; such a set may also be called a unit set.[6] Any such set can be written as {x}, where x is the element. The set {x} and the element x mean different things; Halmos[30] draws the analogy that a box containing a hat is not the same as the hat.

Subsets

Main page: Subset

If every element of set A is also in B, then A is described as being a subset of B, or contained in B, written A ⊆ B,[31] or B ⊇ A.[32] The latter notation may be read B contains A, B includes A, or B is a superset of A. The relationship between sets established by ⊆ is called inclusion or containment. Two sets are equal if they contain each other: A ⊆ B and B ⊆ A is equivalent to A = B.[20]

If A is a subset of B, but A is not equal to B, then A is called a proper subset of B. This can be written A ⊊ B. Likewise, B ⊋ A means B is a proper superset of A, i.e. B contains A, and is not equal to A.

A third pair of operators ⊂ and ⊃ are used differently by different authors: some authors use A ⊂ B and B ⊃ A to mean A is any subset of B (and not necessarily a proper subset),[33][24] while others reserve A ⊂ B and B ⊃ A for cases where A is a proper subset of B.[31]

Examples:

  • The set of all humans is a proper subset of the set of all mammals.
  • {1, 3} ⊂ {1, 2, 3, 4}.
  • {1, 2, 3, 4} ⊆ {1, 2, 3, 4}.

The empty set is a subset of every set,[26] and every set is a subset of itself:[33]

  • ∅ ⊆ A.
  • A ⊆ A.

Euler and Venn diagrams

A is a subset of B.
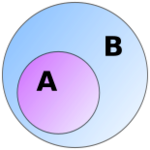
B is a superset of A.

An Euler diagram is a graphical representation of a collection of sets; each set is depicted as a planar region enclosed by a loop, with its elements inside. If A is a subset of B, then the region representing A is completely inside the region representing B. If two sets have no elements in common, the regions do not overlap.

A Venn diagram, in contrast, is a graphical representation of n sets in which the n loops divide the plane into 2n zones such that for each way of selecting some of the n sets (possibly all or none), there is a zone for the elements that belong to all the selected sets and none of the others. For example, if the sets are A, B, and C, there should be a zone for the elements that are inside A and C and outside B (even if such elements do not exist).

Special sets of numbers in mathematics

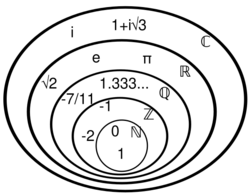
The natural numbers [math]\displaystyle{ \mathbb{N} }[/math] are contained in the integers [math]\displaystyle{ \mathbb{Z} }[/math], which are contained in the rational numbers [math]\displaystyle{ \mathbb{Q} }[/math], which are contained in the real numbers [math]\displaystyle{ \mathbb{R} }[/math], which are contained in the complex numbers [math]\displaystyle{ \mathbb{C} }[/math]

There are sets of such mathematical importance, to which mathematicians refer so frequently, that they have acquired special names and notational conventions to identify them.

Many of these important sets are represented in mathematical texts using bold (e.g. [math]\displaystyle{ \mathbf Z }[/math]) or blackboard bold (e.g. [math]\displaystyle{ \mathbb Z }[/math]) typeface.[34] These include

  • [math]\displaystyle{ \mathbf N }[/math] or [math]\displaystyle{ \mathbb N }[/math], the set of all natural numbers: [math]\displaystyle{ \mathbf N=\{0,1,2,3,...\} }[/math] (often, authors exclude 0);[34]
  • [math]\displaystyle{ \mathbf Z }[/math] or [math]\displaystyle{ \mathbb Z }[/math], the set of all integers (whether positive, negative or zero): [math]\displaystyle{ \mathbf Z=\{...,-2,-1,0,1,2,3,...\} }[/math];[34]
  • [math]\displaystyle{ \mathbf Q }[/math] or [math]\displaystyle{ \mathbb Q }[/math], the set of all rational numbers (that is, the set of all proper and improper fractions): [math]\displaystyle{ \mathbf Q=\left\{\frac {a}{b}\mid a,b\in\mathbf Z,b\ne0\right\} }[/math]. For example, −7/4 ∈ Q and 5 = 5/1 ∈ Q;[34]
  • [math]\displaystyle{ \mathbf R }[/math] or [math]\displaystyle{ \mathbb R }[/math], the set of all real numbers, including all rational numbers and all irrational numbers (which include algebraic numbers such as [math]\displaystyle{ \sqrt2 }[/math] that cannot be rewritten as fractions, as well as transcendental numbers such as π and e);[34]
  • [math]\displaystyle{ \mathbf C }[/math] or [math]\displaystyle{ \mathbb C }[/math], the set of all complex numbers: C = {a + bi | a, b ∈ R}, for example, 1 + 2i ∈ C.[34]

Each of the above sets of numbers has an infinite number of elements. Each is a subset of the sets listed below it.

Sets of positive or negative numbers are sometimes denoted by superscript plus and minus signs, respectively. For example, [math]\displaystyle{ \mathbf{Q}^+ }[/math] represents the set of positive rational numbers.

Functions

A function (or mapping) from a set A to a set B is a rule that assigns to each "input" element of A an "output" that is an element of B; more formally, a function is a special kind of relation, one that relates each element of A to exactly one element of B. A function is called

  • injective (or one-to-one) if it maps any two different elements of A to different elements of B,
  • surjective (or onto) if for every element of B, there is at least one element of A that maps to it, and
  • bijective (or a one-to-one correspondence) if the function is both injective and surjective — in this case, each element of A is paired with a unique element of B, and each element of B is paired with a unique element of A, so that there are no unpaired elements.

An injective function is called an injection, a surjective function is called a surjection, and a bijective function is called a bijection or one-to-one correspondence.

Cardinality

Main page: Cardinality

The cardinality of a set S, denoted ‹See Tfd›|S|, is the number of members of S.[35] For example, if B = {blue, white, red}, then ‹See Tfd›|B| = 3. Repeated members in roster notation are not counted,[36][37] so ‹See Tfd›|{blue, white, red, blue, white}| = 3, too.

More formally, two sets share the same cardinality if there exists a bijection between them.

The cardinality of the empty set is zero.[38]

Infinite sets and infinite cardinality

The list of elements of some sets is endless, or infinite. For example, the set [math]\displaystyle{ \N }[/math] of natural numbers is infinite.[20] In fact, all the special sets of numbers mentioned in the section above are infinite. Infinite sets have infinite cardinality.

Some infinite cardinalities are greater than others. Arguably one of the most significant results from set theory is that the set of real numbers has greater cardinality than the set of natural numbers.[39] Sets with cardinality less than or equal to that of [math]\displaystyle{ \N }[/math] are called countable sets; these are either finite sets or countably infinite sets (sets of the same cardinality as [math]\displaystyle{ \N }[/math]); some authors use "countable" to mean "countably infinite". Sets with cardinality strictly greater than that of [math]\displaystyle{ \N }[/math] are called uncountable sets.

However, it can be shown that the cardinality of a straight line (i.e., the number of points on a line) is the same as the cardinality of any segment of that line, of the entire plane, and indeed of any finite-dimensional Euclidean space.[40]

The continuum hypothesis

Main page: Continuum hypothesis

The continuum hypothesis, formulated by Georg Cantor in 1878, is the statement that there is no set with cardinality strictly between the cardinality of the natural numbers and the cardinality of a straight line.[41] In 1963, Paul Cohen proved that the continuum hypothesis is independent of the axiom system ZFC consisting of Zermelo–Fraenkel set theory with the axiom of choice.[42] (ZFC is the most widely-studied version of axiomatic set theory.)

Power sets

Main page: Power set

The power set of a set S is the set of all subsets of S.[20] The empty set and S itself are elements of the power set of S, because these are both subsets of S. For example, the power set of {1, 2, 3} is {∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}. The power set of a set S is commonly written as P(S) or 2S.[20][43][8]

If S has n elements, then P(S) has 2n elements.[44] For example, {1, 2, 3} has three elements, and its power set has 23 = 8 elements, as shown above.

If S is infinite (whether countable or uncountable), then P(S) is uncountable. Moreover, the power set is always strictly "bigger" than the original set, in the sense that any attempt to pair up the elements of S with the elements of P(S) will leave some elements of P(S) unpaired. (There is never a bijection from S onto P(S).)[45]

Partitions

Main page: Partition of a set

A partition of a set S is a set of nonempty subsets of S, such that every element x in S is in exactly one of these subsets. That is, the subsets are pairwise disjoint (meaning any two sets of the partition contain no element in common), and the union of all the subsets of the partition is S.[46][47]

Basic operations

Main page: Algebra of sets
The complement of A in U

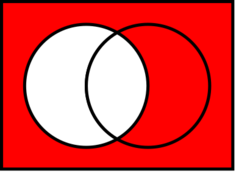
Suppose that a universal set U (a set containing all elements being discussed) has been fixed, and that A is a subset of U.

  • The complement of A is the set of all elements (of U) that do not belong to A. It may be denoted Ac or A′. In set-builder notation, [math]\displaystyle{ A^{\text{c}} = \{a \in U : a \notin A \} }[/math]. The complement may also be called the absolute complement to distinguish it from the relative complement below. Example: If the universal set is taken to be the set of integers, then the complement of the set of even integers is the set of odd integers.
The union of A and B, denoted A ∪ B
The intersection of A and B, denoted A ∩ B
The set difference A \ B
The symmetric difference of A and B

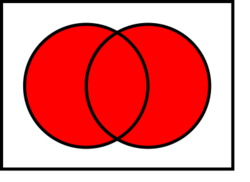
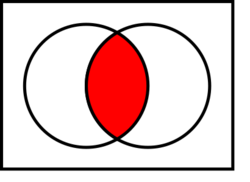
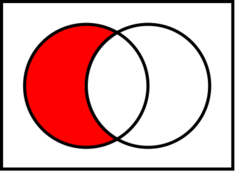
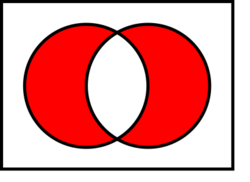
Given any two sets A and B,

  • their union A ∪ B is the set of all things that are members of A or B or both.
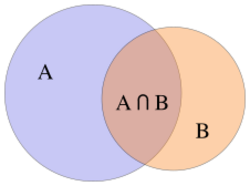
  • their intersection A ∩ B is the set of all things that are members of both A and B. If A ∩ B = ∅, then A and B are said to be disjoint.
  • the set difference A \ B (also written A − B) is the set of all things that belong to A but not B. Especially when B is a subset of A, it is also called the relative complement of B in A. With Bc as the absolute complement of B (in the universal set U), A \ B = A ∩ Bc .
  • their symmetric difference A Δ B is the set of all things that belong to A or B but not both. One has [math]\displaystyle{ A\,\Delta\,B = (A \setminus B) \cup (B \setminus A) }[/math].
  • their cartesian product A × B is the set of all ordered pairs (a,b) such that a is an element of A and b is an element of B.

Examples:

  • {1, 2, 3} ∪ {3, 4, 5} = {1, 2, 3, 4, 5}.
  • {1, 2, 3} ∩ {3, 4, 5} = {3}.
  • {1, 2, 3} − {3, 4, 5} = {1, 2}.
  • {1, 2, 3} Δ {3, 4, 5} = {1, 2, 4, 5}.
  • {a, b} × {1, 2, 3} = {(a,1), (a,2), (a,3), (b,1), (b,2), (b,3)}.

The operations above satisfy many identities. For example, one of De Morgan's laws states that (A ∪ B)′ = A′ ∩ B′ (that is, the elements outside the union of A and B are the elements that are outside A and outside B).

The cardinality of A × B is the product of the cardinalities of A and B. (This is an elementary fact when A and B are finite. When one or both are infinite, multiplication of cardinal numbers is defined to make this true.)

The power set of any set becomes a Boolean ring with symmetric difference as the addition of the ring and intersection as the multiplication of the ring.

Applications

Sets are ubiquitous in modern mathematics. For example, structures in abstract algebra, such as groups, fields and rings, are sets closed under one or more operations.

One of the main applications of naive set theory is in the construction of relations. A relation from a domain A to a codomain B is a subset of the Cartesian product A × B. For example, considering the set S = {rock, paper, scissors} of shapes in the game of the same name, the relation "beats" from S to S is the set B = {(scissors,paper), (paper,rock), (rock,scissors)}; thus x beats y in the game if the pair (x,y) is a member of B. Another example is the set F of all pairs (x, x2), where x is real. This relation is a subset of R × R, because the set of all squares is subset of the set of all real numbers. Since for every x in R, one and only one pair (x,...) is found in F, it is called a function. In functional notation, this relation can be written as F(x) = x2.

Principle of inclusion and exclusion

Main page: Inclusion–exclusion principle
The inclusion-exclusion principle for two finite sets states that the size of their union is the sum of the sizes of the sets minus the size of their intersection.

The inclusion–exclusion principle is a technique for counting the elements in a union of two finite sets in terms of the sizes of the two sets and their intersection. It can be expressed symbolically as [math]\displaystyle{ |A \cup B| = |A| + |B| - |A \cap B|. }[/math]

A more general form of the principle gives the cardinality of any finite union of finite sets: [math]\displaystyle{ \begin{align} \left|A_{1}\cup A_{2}\cup A_{3}\cup\ldots\cup A_{n}\right|=& \left(\left|A_{1}\right|+\left|A_{2}\right|+\left|A_{3}\right|+\ldots\left|A_{n}\right|\right) \\ &{} - \left(\left|A_{1}\cap A_{2}\right|+\left|A_{1}\cap A_{3}\right|+\ldots\left|A_{n-1}\cap A_{n}\right|\right) \\ &{} + \ldots \\ &{} + \left(-1\right)^{n-1}\left(\left|A_{1}\cap A_{2}\cap A_{3}\cap\ldots\cap A_{n}\right|\right). \end{align} }[/math]


History

Main page: Set theory

The concept of a set emerged in mathematics at the end of the 19th century.[48] The German word for set, Menge, was coined by Bernard Bolzano in his work Paradoxes of the Infinite.[49][50][51]

Passage with a translation of the original set definition of Georg Cantor. The German word Menge for set is translated with aggregate here.

Georg Cantor, one of the founders of set theory, gave the following definition at the beginning of his Beiträge zur Begründung der transfiniten Mengenlehre:[52][1]

A set is a gathering together into a whole of definite, distinct objects of our perception or our thought—which are called elements of the set.

Bertrand Russell introduced the distinction between a set and a class (a set is a class, but some classes, such as the class of all sets, are not sets; see Russell's paradox):[53]

When mathematicians deal with what they call a manifold, aggregate, Menge, ensemble, or some equivalent name, it is common, especially where the number of terms involved is finite, to regard the object in question (which is in fact a class) as defined by the enumeration of its terms, and as consisting possibly of a single term, which in that case is the class.

Naive set theory

Main page: Naive set theory

The foremost property of a set is that it can have elements, also called members. Two sets are equal when they have the same elements. More precisely, sets A and B are equal if every element of A is an element of B, and every element of B is an element of A; this property is called the extensionality of sets.[23]

The simple concept of a set has proved enormously useful in mathematics, but paradoxes arise if no restrictions are placed on how sets can be constructed:

  • Russell's paradox shows that the "set of all sets that do not contain themselves", i.e., {x | x is a set and x ∉ x}, cannot exist.
  • Cantor's paradox shows that "the set of all sets" cannot exist.

Naïve set theory defines a set as any well-defined collection of distinct elements, but problems arise from the vagueness of the term well-defined.

Axiomatic set theory

In subsequent efforts to resolve these paradoxes since the time of the original formulation of naïve set theory, the properties of sets have been defined by axioms. Axiomatic set theory takes the concept of a set as a primitive notion.[54] The purpose of the axioms is to provide a basic framework from which to deduce the truth or falsity of particular mathematical propositions (statements) about sets, using first-order logic. According to Gödel's incompleteness theorems however, it is not possible to use first-order logic to prove any such particular axiomatic set theory is free from paradox.[citation needed]

See also


Notes

  1. ↑ 1.0 1.1 Cantor, Georg; Jourdain, ((Philip E.B. (Translator))) (1915). Contributions to the founding of the theory of transfinite numbers. New York Dover Publications (1954 English translation). "By an 'aggregate' (Menge) we are to understand any collection into a whole (Zusammenfassung zu einem Ganzen) M of definite and separate objects m of our intuition or our thought."  Here: p.85
  2. ↑ P. K. Jain; Khalil Ahmad; Om P. Ahuja (1995). Functional Analysis. New Age International. p. 1. ISBN 978-81-224-0801-0. https://books.google.com/books?id=yZ68h97pnAkC&pg=PA1. 
  3. ↑ Samuel Goldberg (1 January 1986). Probability: An Introduction. Courier Corporation. p. 2. ISBN 978-0-486-65252-8. https://books.google.com/books?id=CmzFx9rB_FcC&pg=PA2. 
  4. ↑ Thomas H. Cormen; Charles E Leiserson; Ronald L Rivest; Clifford Stein (2001). Introduction To Algorithms. MIT Press. p. 1070. ISBN 978-0-262-03293-3. https://books.google.com/books?id=NLngYyWFl_YC&pg=PA1070. 
  5. ↑ 5.0 5.1 5.2 Halmos 1960, p. 1.
  6. ↑ 6.0 6.1 Stoll, Robert (1974). Sets, Logic and Axiomatic Theories. W. H. Freeman and Company. pp. 5. ISBN 9780716704577. https://archive.org/details/setslogicaxiomat0000stol. 
  7. ↑ Seymor Lipschutz; Marc Lipson (22 June 1997). Schaum's Outline of Discrete Mathematics. McGraw Hill Professional. p. 1. ISBN 978-0-07-136841-4. https://books.google.com/books?id=6A5g3RiYiBUC&pg=PA1. 
  8. ↑ 8.0 8.1 8.2 "Introduction to Sets". https://www.mathsisfun.com/sets/sets-introduction.html. 
  9. ↑ Charles Roberts (24 June 2009). Introduction to Mathematical Proofs: A Transition. CRC Press. p. 45. ISBN 978-1-4200-6956-3. https://books.google.com/books?id=NjBLnLyE4jAC&pg=PA45. 
  10. ↑ David Johnson; David B. Johnson; Thomas A. Mowry (June 2004). Finite Mathematics: Practical Applications (Docutech Version). W. H. Freeman. p. 220. ISBN 978-0-7167-6297-3. https://books.google.com/books?id=ZQAqzxLFXhoC&pg=PA220. 
  11. ↑ Ignacio Bello; Anton Kaul; Jack R. Britton (29 January 2013). Topics in Contemporary Mathematics. Cengage Learning. p. 47. ISBN 978-1-133-10742-2. https://books.google.com/books?id=d8Se_8DWTQ4C&pg=PA47. 
  12. ↑ Susanna S. Epp (4 August 2010). Discrete Mathematics with Applications. Cengage Learning. p. 13. ISBN 978-0-495-39132-6. https://books.google.com/books?id=PPc_2qUhXrAC&pg=PA13. 
  13. ↑ A. Kanamori, "The Empty Set, the Singleton, and the Ordered Pair", p.278. Bulletin of Symbolic Logic vol. 9, no. 3, (2003). Accessed 21 August 2023.
  14. ↑ Stephen B. Maurer; Anthony Ralston (21 January 2005). Discrete Algorithmic Mathematics. CRC Press. p. 11. ISBN 978-1-4398-6375-6. https://books.google.com/books?id=_0vNBQAAQBAJ&pg=PA11. 
  15. ↑ D. Van Dalen; H. C. Doets; H. De Swart (9 May 2014). Sets: Naïve, Axiomatic and Applied: A Basic Compendium with Exercises for Use in Set Theory for Non Logicians, Working and Teaching Mathematicians and Students. Elsevier Science. p. 1. ISBN 978-1-4831-5039-0. https://books.google.com/books?id=PfbiBQAAQBAJ&pg=PA1. 
  16. ↑ Alfred Basta; Stephan DeLong; Nadine Basta (1 January 2013). Mathematics for Information Technology. Cengage Learning. p. 3. ISBN 978-1-285-60843-3. https://books.google.com/books?id=VUYLAAAAQBAJ&pg=PA3. 
  17. ↑ Laura Bracken; Ed Miller (15 February 2013). Elementary Algebra. Cengage Learning. p. 36. ISBN 978-0-618-95134-5. https://books.google.com/books?id=nFkrl_kDiTAC&pg=PA36. 
  18. ↑ Halmos 1960, p. 4.
  19. ↑ 19.0 19.1 19.2 Frank Ruda (6 October 2011). Hegel's Rabble: An Investigation into Hegel's Philosophy of Right. Bloomsbury Publishing. p. 151. ISBN 978-1-4411-7413-0. https://books.google.com/books?id=VV0SBwAAQBAJ&pg=PA151. 
  20. ↑ 20.0 20.1 20.2 20.3 20.4 John F. Lucas (1990). Introduction to Abstract Mathematics. Rowman & Littlefield. p. 108. ISBN 978-0-912675-73-2. https://books.google.com/books?id=jklsb5JUgoQC&pg=PA108. 
  21. ↑ Weisstein, Eric W.. "Set" (in en). https://mathworld.wolfram.com/Set.html. 
  22. ↑ Ralph C. Steinlage (1987). College Algebra. West Publishing Company. ISBN 978-0-314-29531-6. https://books.google.com/books?id=lcg3gY3444IC. 
  23. ↑ 23.0 23.1 Halmos 1960, p. 2.
  24. ↑ 24.0 24.1 Marek Capinski; Peter E. Kopp (2004). Measure, Integral and Probability. Springer Science & Business Media. p. 2. ISBN 978-1-85233-781-0. https://books.google.com/books?id=jdnGYuh58YUC&pg=PA2. 
  25. ↑ "Set Symbols". https://www.mathsisfun.com/sets/symbols.html. 
  26. ↑ 26.0 26.1 Halmos 1960, p. 8.
  27. ↑ K.T. Leung; Doris Lai-chue Chen (1 July 1992). Elementary Set Theory, Part I/II. Hong Kong University Press. p. 27. ISBN 978-962-209-026-2. https://books.google.com/books?id=cdmy2eOhJdkC&pg=PA27. 
  28. ↑ Aggarwal, M.L. (2021). "1. Sets". Understanding ISC Mathematics Class XI. 1. Arya Publications (Avichal Publishing Company). p. A=3. 
  29. ↑ Sourendra Nath, De (January 2015). "Unit-1 Sets and Functions: 1. Set Theory". Chhaya Ganit (Ekadash Shreni). Scholar Books Pvt. Ltd.. p. 5. 
  30. ↑ Halmos 1960, Sect.2.
  31. ↑ 31.0 31.1 Felix Hausdorff (2005). Set Theory. American Mathematical Soc.. p. 30. ISBN 978-0-8218-3835-8. https://books.google.com/books?id=yvVIdH16k0YC&pg=PA30. 
  32. ↑ Peter Comninos (6 April 2010). Mathematical and Computer Programming Techniques for Computer Graphics. Springer Science & Business Media. p. 7. ISBN 978-1-84628-292-8. https://books.google.com/books?id=Kdb7-YnnOVwC&pg=PA7. 
  33. ↑ 33.0 33.1 Halmos 1960, p. 3.
  34. ↑ 34.0 34.1 34.2 34.3 34.4 34.5 George Tourlakis (13 February 2003). Lectures in Logic and Set Theory: Volume 2, Set Theory. Cambridge University Press. pp. 137. ISBN 978-1-139-43943-5. https://books.google.com/books?id=nparMXao59QC&pg=PA137. 
  35. ↑ Yiannis N. Moschovakis (1994). Notes on Set Theory. Springer Science & Business Media. ISBN 978-3-540-94180-4. https://books.google.com/books?id=ndx0_6VCypcC. 
  36. ↑ Arthur Charles Fleck (2001). Formal Models of Computation: The Ultimate Limits of Computing. World Scientific. p. 3. ISBN 978-981-02-4500-9. https://books.google.com/books?id=c42oYf4zBzMC&pg=PA3. 
  37. ↑ William Johnston (25 September 2015). The Lebesgue Integral for Undergraduates. The Mathematical Association of America. p. 7. ISBN 978-1-939512-07-9. https://books.google.com/books?id=v4ueCgAAQBAJ&pg=PA7. 
  38. ↑ Karl J. Smith (7 January 2008). Mathematics: Its Power and Utility. Cengage Learning. p. 401. ISBN 978-0-495-38913-2. https://books.google.com/books?id=-0x2JszrkooC&pg=PA401. 
  39. ↑ John Stillwell (16 October 2013). The Real Numbers: An Introduction to Set Theory and Analysis. Springer Science & Business Media. ISBN 978-3-319-01577-4. https://books.google.com/books?id=VPe8BAAAQBAJ. 
  40. ↑ David Tall (11 April 2006). Advanced Mathematical Thinking. Springer Science & Business Media. pp. 211. ISBN 978-0-306-47203-9. https://books.google.com/books?id=czKqBgAAQBAJ&pg=PA212. 
  41. ↑ Cantor, Georg (1878). "Ein Beitrag zur Mannigfaltigkeitslehre". Journal für die Reine und Angewandte Mathematik 1878 (84): 242–258. doi:10.1515/crll.1878.84.242. http://www.digizeitschriften.de/dms/img/?PPN=PPN243919689_0084&DMDID=dmdlog15. 
  42. ↑ Cohen, Paul J. (December 15, 1963). "The Independence of the Continuum Hypothesis". Proceedings of the National Academy of Sciences of the United States of America 50 (6): 1143–1148. doi:10.1073/pnas.50.6.1143. PMID 16578557. Bibcode: 1963PNAS...50.1143C. 
  43. ↑ Halmos 1960, p. 19.
  44. ↑ Halmos 1960, p. 20.
  45. ↑ Edward B. Burger; Michael Starbird (18 August 2004). The Heart of Mathematics: An invitation to effective thinking. Springer Science & Business Media. p. 183. ISBN 978-1-931914-41-3. https://books.google.com/books?id=M-qK8anbZmwC&pg=PA183. 
  46. ↑ Toufik Mansour (27 July 2012). Combinatorics of Set Partitions. CRC Press. ISBN 978-1-4398-6333-6. https://books.google.com/books?id=5NvrH4w8WGsC. 
  47. ↑ Halmos 1960, p. 28.
  48. ↑ José Ferreirós (16 August 2007). Labyrinth of Thought: A History of Set Theory and Its Role in Modern Mathematics. Birkhäuser Basel. ISBN 978-3-7643-8349-7. https://books.google.com/books?id=TXRBwwEACAAJ. 
  49. ↑ Steve Russ (9 December 2004). The Mathematical Works of Bernard Bolzano. OUP Oxford. ISBN 978-0-19-151370-1. https://books.google.com/books?id=zp7cLQn0x3gC&pg=PR28. 
  50. ↑ William Ewald; William Bragg Ewald (1996). From Kant to Hilbert Volume 1: A Source Book in the Foundations of Mathematics. OUP Oxford. p. 249. ISBN 978-0-19-850535-8. https://books.google.com/books?id=rykSDAAAQBAJ&pg=PA249. 
  51. ↑ Paul Rusnock; Jan Sebestík (25 April 2019). Bernard Bolzano: His Life and Work. OUP Oxford. p. 430. ISBN 978-0-19-255683-7. https://books.google.com/books?id=-hqJDwAAQBAJ&pg=PA430. 
  52. ↑ Georg Cantor (Nov 1895). "Beiträge zur Begründung der transfiniten Mengenlehre (1)" (in German). Mathematische Annalen 46 (4): 481–512. http://www.digizeitschriften.de/dms/resolveppn/?PID=GDZPPN00225557X. 
  53. ↑ Bertrand Russell (1903) The Principles of Mathematics, chapter VI: Classes
  54. ↑ Jose Ferreiros (1 November 2001). Labyrinth of Thought: A History of Set Theory and Its Role in Modern Mathematics. Springer Science & Business Media. ISBN 978-3-7643-5749-8. https://books.google.com/books?id=DITy0nsYQQoC. 

References

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Set_(mathematics)&oldid=3373192"
Licensed under CC BY-SA 3.0 | Source: https://handwiki.org/wiki/Set_(mathematics)
40 views | Status: cached on July 14 2024 14:15:36
↧ Download this article as ZWI file
Encyclosphere.org EncycloReader is supported by the EncyclosphereKSF