Shabal

Shabal is a cryptographic hash function submitted by the France-funded research project Saphir to NIST's international competition on hash functions.

Saphir partners

The research partners of Saphir (with the exception of LIENS) initiated the conception of Shabal and were later joined by partners of the research project Saphir2 who actively contributed to the final design of Shabal. Saphir (Security and Analysis of Hash Primitives) is an ANR funded project on hash functions. Saphir has started in March 2006 for a duration of three years and brought five partners together: Cryptolog International, DCSSI, France Telecom (leader), Gemalto and LIENS. Partners of Saphir2 come from both industry and academia; in addition to partners of Saphir, 4 new partners: EADS SN, INRIA, Sagem Sécurité and UVSQ joined and contributed to the project.^[1]

History

Shabal was an entry in the NIST hash function competition, where it passed to the second round, but failed to enter the final round. Shabal was not selected as a finalist mainly due to security concerns. Although the security of the full hash algorithm was not compromised, the discovery of non-randomness properties with low time complexities raised concerns among NIST's cryptographers about the possibility of more powerful attacks in the future.^[2]

The name of the algorithm was chosen as a tribute to Sébastien Chabal.^[1]

Description

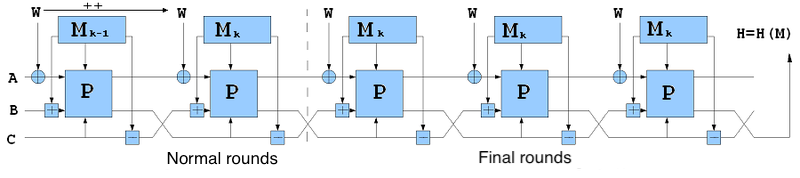
Shabal uses a mode of operation that can be considered as a variant of a wide-pipe, Merkle–Damgård hash construction. The internal state of Shabal consists of three parts, denoted as A, B and C. The keyed permutation of Shabal updates A and B using nonlinear feedback shift registers that interact with each other. The main loop of the permutation uses modular multiplication by three and five, modular addition, XOR, complementation, and AND operations.

The chaining mode of Shabal works as follows: (A, B) ← PM,C

(A, B, C) ← (A, C – M, B),

(A ⊕ W, B + M),

where M is the message block, and W is the counter. After processing all message blocks, three finalization rounds are applied in which the message block and the counter values are fixed. Two tunable parameters (p, r) are defined for Shabal, where p is the number of loops performed within the key permutation, and r is the size of A. The default value of (p, r) is (3, 12). Additionally, p and r should satisfy 16p ≡ 0 mod r. The same internal function is used for all output sizes of Shabal.^[2]

Output sizes of Shabal

Output sizes of Shabal, based on length of the digest are:

• Shabal-192
• Shabal-224
• Shabal-256
• Shabal-384
• Shabal-512^[1]

Outputs of Shabal

Example Shabal hashes:

• Shabal-192: CB6E700F CE4DCF97 D2BBBF00 0C5364FB B40C8732 0D733948
• Shabal-224: 14A6DD99 E8D207F9 F7187681 326F6930 8BCAAE00 25F4855F 3120BA43
• Shabal-256: C0088FDA 9ABA672A 79D0BD56 07AE488E 095E2114 06855B3B 1877A349 A2543F99
• Shabal-384: 3312DE9D DA850D91 03785C3A C611B112 5D1BCAFC 033755D2 3B8EE05E 15251E4E 636A724F F0A8E584 4AABEAAF 122FC0C4
• Shabal-512: C6168015 0A3F1FC8 688DD952 8E9E2FED 23EF9578 BCE2A7CB A5D80961 E6C9E632 9701A5A6 F037B89F 20C6C44E DC7931E7 2BB5AB82 B3ADCD32 9CE25056 22305E98^[1]

Security

• Various distinguishers have been proposed for the permutation of Shabal. Using cube testers, a statistical non-randomness property of Shabal's key permutation was described with time complexity 2³⁰⁰.^[3]
• A rotational distinguisher to the keyed permutation of Shabal using 2¹⁷¹ calls was presented. The distinguisher is based on the observation that most of the operations in P preserve rotational relationships between inputs. However, the attack cannot be extended to the hash algorithm, due to the non-symmetric IV, the addition of the block counter and the existence of the finalization rounds.^[4][5]
• Another distinguisher was presented, based on the observation that multiplication by three preserves the difference in the most significant bit with probability one. Using this observation, the authors presented a method to find semi-equivalent keys for the keyed permutation. Under the related-key model, the authors also presented a method that distinguishes P from a random permutation using a single query. The method can be generalized to any security parameter. The authors also presented a method to find pseudo-collisions and pseudosecond-preimages for a variant of Shabal in which the number of iterations in the finalization is 24N (N ≥ 2), instead of 36. However, this attack does not work for the original Shabal, since it is not possible to cancel out the differences when the number of iterations is 36.^[6]
• Some non-randomness properties were shown for the keyed permutation P that are easy to verify. The authors proposed a simple method to find fixed points in P. The inputs to the permutation were selected so that they are not affected by the loops in the permutation. The method is independent of the number of words in A and the number of rounds; therefore, the method works for any choice of the tunable security parameters. The authors also showed a way to construct many, large multi-collisions, where the only difference is in the key input.^[2]
• A distinguisher was presented over some of the biased output bits using differential analysis with 2²³ data complexity.^[7]
• A low weight (45-bit) pseudo-collision attack on the Shabal compression function with time complexity 2⁸⁴ was presented. A preimage attack with 2⁴⁹⁷ time and 2⁴⁰⁰ memory complexity for Shabal 512 using security parameters (2, 12).^[8]
• None of the distinguishers directly threatens the claimed security of the hash algorithm. Moreover, the designers have modified the indifferentiability security proof of their chaining mode to require weaker assumptions than ideal ciphers.^[2]

Implementations

• CodePlex Hashlib (C)
• MetaCPAN - Digest-Shabal-0.05 (C, Perl)
• Burstcoin (Java)
• crates.io - shabal (Rust)

References

External links

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Shabal. Read more