Shekel function
From HandWiki - Reading time: 1 min
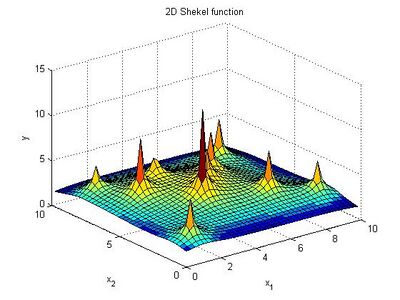
The Shekel function or also Shekel's foxholes is a multidimensional, multimodal, continuous, deterministic function commonly used as a test function for testing optimization techniques.[1]
The mathematical form of a function in [math]\displaystyle{ n }[/math] dimensions with [math]\displaystyle{ m }[/math] maxima is:
[math]\displaystyle{ f(\vec{x}) = \sum_{i = 1}^{m} \; \left( c_{i} + \sum\limits_{j = 1}^{n} (x_{j} - a_{ji})^2 \right)^{-1} }[/math]
or, similarly,
[math]\displaystyle{ f(x_1,x_2,...,x_{n-1},x_n) = \sum_{i = 1}^{m} \; \left( c_{i} + \sum\limits_{j = 1}^{n} (x_{j} - a_{ij})^2 \right)^{-1} }[/math]
Global minima
Numerically certified global minima and the corresponding solutions were obtained using interval methods for up to [math]\displaystyle{ n = 10 }[/math].[2]
See also
References
- ↑ Molga, M.; Smutnicki, C. (2005). "Test functions for optimization needs. Test functions for optimization needs". Test Functions for Optimization Needs 101: 48. https://marksmannet.com/RobertMarks/Classes/ENGR5358/Papers/functions.pdf.
- ↑ Vanaret C. (2015) Hybridization of interval methods and evolutionary algorithms for solving difficult optimization problems. PhD thesis. Ecole Nationale de l'Aviation Civile. Institut National Polytechnique de Toulouse, France.
Further reading
Shekel, J. 1971. "Test Functions for Multimodal Search Techniques." Fifth Annual Princeton Conference on Information Science and Systems.
 |  |
EncycloReader
is supported by the 
KSF