Sigma approximation

Animation of the additive synthesis of a square wave with an increasing number of harmonics by way of the σ-approximation

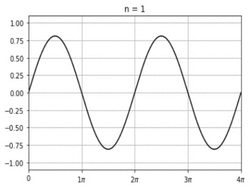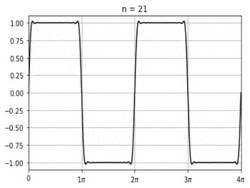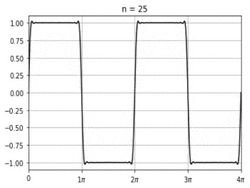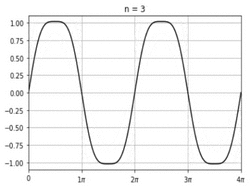
In mathematics, σ-approximation adjusts a Fourier summation to greatly reduce the Gibbs phenomenon, which would otherwise occur at discontinuities.^[1][2]

A σ-approximated summation for a series of period T can be written as follows: [math]\displaystyle{ s(\theta) = \frac{1}{2} a_0 + \sum_{k=1}^{m-1} \operatorname{sinc} \frac{k}{m} \cdot \left[a_{k} \cos \left( \frac{2 \pi k}{T} \theta \right) + b_k \sin \left( \frac{2 \pi k}{T} \theta \right) \right], }[/math] in terms of the normalized sinc function [math]\displaystyle{ \operatorname{sinc} x = \frac{\sin \pi x}{\pi x}. }[/math]

The term [math]\displaystyle{ \operatorname{sinc} \frac{k}{m} }[/math] is the Lanczos σ factor, which is responsible for eliminating most of the Gibbs phenomenon. It does not do so entirely, however, but one can square or even cube the expression to serially attenuate Gibbs phenomenon in the most extreme cases.

See also

• Lanczos resampling

References

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Sigma approximation. Read more