Spectral graph theory

In mathematics, spectral graph theory is the study of the properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated with the graph, such as its adjacency matrix or Laplacian matrix.

The adjacency matrix of a simple undirected graph is a real symmetric matrix and is therefore orthogonally diagonalizable; its eigenvalues are real algebraic integers.

While the adjacency matrix depends on the vertex labeling, its spectrum is a graph invariant, although not a complete one.

Spectral graph theory is also concerned with graph parameters that are defined via multiplicities of eigenvalues of matrices associated to the graph, such as the Colin de Verdière number.

Cospectral graphs

Two graphs are called cospectral or isospectral if the adjacency matrices of the graphs are isospectral, that is, if the adjacency matrices have equal multisets of eigenvalues.

Two cospectral enneahedra, the smallest possible cospectral polyhedral graphs

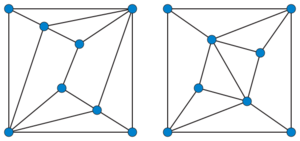
Cospectral graphs need not be isomorphic, but isomorphic graphs are always cospectral.

Graphs determined by their spectrum

A graph [math]\displaystyle{ G }[/math] is said to be determined by its spectrum if any other graph with the same spectrum as [math]\displaystyle{ G }[/math] is isomorphic to [math]\displaystyle{ G }[/math].

Some first examples of families of graphs that are determined by their spectrum include:

• The complete graphs.
• The finite starlike trees.

Cospectral mates

A pair of graphs are said to be cospectral mates if they have the same spectrum, but are non-isomorphic.

The smallest pair of cospectral mates is {K_1,4, C₄ ∪ K₁}, comprising the 5-vertex star and the graph union of the 4-vertex cycle and the single-vertex graph, as reported by Collatz and Sinogowitz^[1][2] in 1957.

The smallest pair of polyhedral cospectral mates are enneahedra with eight vertices each.^[3]

Finding cospectral graphs

Almost all trees are cospectral, i.e., as the number of vertices grows, the fraction of trees for which there exists a cospectral tree goes to 1.^[4]

A pair of regular graphs are cospectral if and only if their complements are cospectral.^[5]

A pair of distance-regular graphs are cospectral if and only if they have the same intersection array.

Cospectral graphs can also be constructed by means of the Sunada method.^[6]

Another important source of cospectral graphs are the point-collinearity graphs and the line-intersection graphs of point-line geometries. These graphs are always cospectral but are often non-isomorphic.^[7]

Cheeger inequality

The famous Cheeger's inequality from Riemannian geometry has a discrete analogue involving the Laplacian matrix; this is perhaps the most important theorem in spectral graph theory and one of the most useful facts in algorithmic applications. It approximates the sparsest cut of a graph through the second eigenvalue of its Laplacian.

Cheeger constant

Main page: Cheeger constant (graph theory)

The Cheeger constant (also Cheeger number or isoperimetric number) of a graph is a numerical measure of whether or not a graph has a "bottleneck". The Cheeger constant as a measure of "bottleneckedness" is of great interest in many areas: for example, constructing well-connected networks of computers, card shuffling, and low-dimensional topology (in particular, the study of hyperbolic 3-manifolds).

More formally, the Cheeger constant h(G) of a graph G on n vertices is defined as

[math]\displaystyle{ h(G) = \min_{0 \lt |S| \le \frac{n}{2} } \frac{|\partial(S)|}{|S|}, }[/math]

where the minimum is over all nonempty sets S of at most n/2 vertices and ∂(S) is the edge boundary of S, i.e., the set of edges with exactly one endpoint in S.^[8]

Cheeger inequality

When the graph G is d-regular, there is a relationship between h(G) and the spectral gap d − λ₂ of G. An inequality due to Dodziuk^[9] and independently Alon and Milman^[10] states that^[11]

[math]\displaystyle{ \frac{1}{2}(d - \lambda_2) \le h(G) \le \sqrt{2d(d - \lambda_2)}. }[/math]

This inequality is closely related to the Cheeger bound for Markov chains and can be seen as a discrete version of Cheeger's inequality in Riemannian geometry.

For general connected graphs that are not necessarily regular, an alternative inequality is given by Chung^[12]:35

[math]\displaystyle{ \frac{1}{2} {\lambda} \le {\mathbf h}(G) \le \sqrt{2 \lambda}, }[/math]

where [math]\displaystyle{ \lambda }[/math] is the least nontrivial eigenvalue of the normalized Laplacian, and [math]\displaystyle{ {\mathbf h}(G) }[/math] is the (normalized) Cheeger constant

[math]\displaystyle{ {\mathbf h}(G) = \min_{\emptyset \not =S\subset V(G)}\frac{|\partial(S)|}{\min({\mathrm{vol}}(S), {\mathrm{vol}}(\bar{S}))} }[/math]

where [math]\displaystyle{ {\mathrm{vol}}(Y) }[/math] is the sum of degrees of vertices in [math]\displaystyle{ Y }[/math].

Hoffman–Delsarte inequality

There is an eigenvalue bound for independent sets in regular graphs, originally due to Alan J. Hoffman and Philippe Delsarte.^[13]

Suppose that [math]\displaystyle{ G }[/math] is a [math]\displaystyle{ k }[/math]-regular graph on [math]\displaystyle{ n }[/math] vertices with least eigenvalue [math]\displaystyle{ \lambda_{\mathrm{min}} }[/math]. Then:[math]\displaystyle{ \alpha(G) \leq \frac{n}{1 - \frac{k}{\lambda_{\mathrm{min}}}} }[/math]where [math]\displaystyle{ \alpha(G) }[/math] denotes its independence number.

This bound has been applied to establish e.g. algebraic proofs of the Erdős–Ko–Rado theorem and its analogue for intersecting families of subspaces over finite fields.^[14]

For general graphs which are not necessarily regular, a similar upper bound for the independence number can be derived by using the maximum eigenvalue [math]\displaystyle{ \lambda'_{max} }[/math] of the normalized Laplacian^[12] of [math]\displaystyle{ G }[/math]: [math]\displaystyle{ \alpha(G) \leq n (1-\frac {1}{\lambda'_{\mathrm{max}}}) \frac {\mathrm{max deg}}{\mathrm{min deg}} }[/math] where [math]\displaystyle{ {\mathrm{max deg}} }[/math] and [math]\displaystyle{ {\mathrm{min deg}} }[/math] denote the maximum and minimum degree in [math]\displaystyle{ G }[/math], respectively. This a consequence of a more general inequality (pp. 109 in ^[12]): [math]\displaystyle{ {\mathrm{vol}}(X) \leq (1-\frac {1}{\lambda'_{\mathrm{max}}}) {\mathrm{vol}}(V(G)) }[/math] where [math]\displaystyle{ X }[/math] is an independent set of vertices and [math]\displaystyle{ {\mathrm{vol}}(Y) }[/math] denotes the sum of degrees of vertices in [math]\displaystyle{ Y }[/math] .

Historical outline

Spectral graph theory emerged in the 1950s and 1960s. Besides graph theoretic research on the relationship between structural and spectral properties of graphs, another major source was research in quantum chemistry, but the connections between these two lines of work were not discovered until much later.^[15] The 1980 monograph Spectra of Graphs^[16] by Cvetković, Doob, and Sachs summarised nearly all research to date in the area. In 1988 it was updated by the survey Recent Results in the Theory of Graph Spectra.^[17] The 3rd edition of Spectra of Graphs (1995) contains a summary of the further recent contributions to the subject.^[15] Discrete geometric analysis created and developed by Toshikazu Sunada in the 2000s deals with spectral graph theory in terms of discrete Laplacians associated with weighted graphs,^[18] and finds application in various fields, including shape analysis. In most recent years, the spectral graph theory has expanded to vertex-varying graphs often encountered in many real-life applications.^{[19][20][21][22]}

See also

• Strongly regular graph
• Algebraic connectivity
• Algebraic graph theory
• Spectral clustering
• Spectral shape analysis
• Estrada index
• Lovász theta
• Expander graph

References

• Alon; Spencer (2011), The probabilistic method, Wiley .
• Brouwer, Andries; Haemers, Willem H. (2011), Spectra of Graphs, Springer, http://www.win.tue.nl/~aeb/2WF02/spectra.pdf 
• Hoory; Linial; Wigderson (2006), Expander graphs and their applications, https://www.cs.huji.ac.il/~nati/PAPERS/expander_survey.pdf 
• Chung, Fan (1997). American Mathematical Society. ed. Spectral Graph Theory. Providence, R. I.. ISBN 0821803158. http://www.math.ucsd.edu/~fan/research/revised.html[first 4 chapters are available in the website] 
• Schwenk, A. J. (1973). "Almost All Trees are Cospectral". in Harary, Frank. New Directions in the Theory of Graphs. New York: Academic Press. ISBN 012324255X. OCLC 890297242. 

External links

• Spielman, Daniel (2011). "Spectral Graph Theory". http://www.cs.yale.edu/~spielman/PAPERS/SGTChapter.pdf.  [chapter from Combinatorial Scientific Computing]
• Spielman, Daniel (2007). "Spectral Graph Theory and its Applications". http://cs-www.cs.yale.edu/homes/spielman/sgta/.  [presented at FOCS 2007 Conference]
• Spielman, Daniel (2004). "Spectral Graph Theory and its Applications". http://www.cs.yale.edu/homes/spielman/eigs/.  [course page and lecture notes]

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Spectral graph theory. Read more